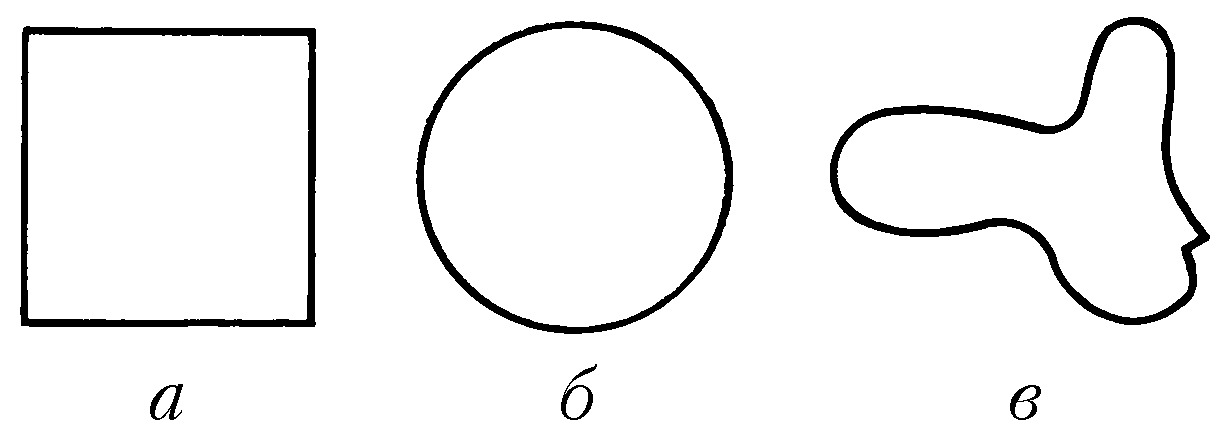ГРУПП ТЕО́РИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ГРУПП ТЕО́РИЯ, раздел алгебры, изучающий в самой общей форме свойства действий (операций), наиболее часто встречающихся в математике и её приложениях. Примерами таких действий являются умножение и сложение чисел, сложение векторов, последовательное выполнение преобразований и т. п. При этом Г. т. изучает не произвольные операции, а лишь те, которые обладают рядом свойств, перечисляемых в определении группы.
Общее (формальное) определение группы таково. Пусть $G$ – произвольное множество, на котором задана бинарная операция, т. е. для любых двух элементов $a$, $b$ из $G$ определён некоторый элемент (обозначаемый, напр., $a \circ b$), который также принадлежит $G$. Если при этом выполняются условия: 1) $(a \circ b) \circ c=a \circ (b \circ c)$ для любых $a$,$b$,$c$ из $G$; 2) в $G$ существует такой элемент $e$ (называемый единицей, иногда – нейтральным элементом), что $a \circ e=e \circ a=a$ для любого $a$ из $G$; 3) для любого $a$ из $G$ существует такой элемент $a^{-1}$ (обратный к $a$ элемент), что $a \circ a^{-1}=a^{-1} \circ a=e$, то множество $G$ с заданной на нём операцией (композицией) $\circ$ называется группой.
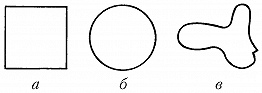
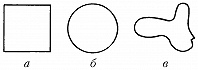
Примеры групп. 1. Множество $G$ разл. движений евклидовой плоскости, самосовмещающих данную фигуру, т. е. переводящих её саму в себя, операцией на котором служит композиция движений (если $\varphi$, $\psi$ – два движения из $G$, то результатом их композиции называется движение $\varphi \circ \psi$ , равносильное последовательному выполнению сначала движения $\varphi$, а затем движения $\psi$), образует т. н. группу симметрий фигуры. Единицей в этой группе является тождественное преобразование плоскости, а обратным к $\varphi$ элементом – обратное к $\varphi$ преобразование. Группа $G$ является характеристикой большей или меньшей симметричности фигуры: чем шире множество $G$, тем симметричнее фигура. Напр., группа симметрий квадрата (рис., а) состоит из восьми движений (четыре поворота вокруг центра квадрата и четыре отражения: два – относительно диагоналей и два – относительно прямых, соединяющих середины противоположных сторон). Для круга (рис., б) группа симметрий содержит бесконечно много элементов (напр., все повороты вокруг центра), а для фигуры, изображённой на рис. (в), группа симметрий состоит из одного тождественного преобразования.
2. Если $\boldsymbol Z$ – множество целых чисел, а операция на $\boldsymbol Z$ – их обычное сложение +, то $\boldsymbol Z$ – группа. Роль $e$ играет число 0, а роль обратного к $z$ элемента – число $-z$. Часть $H$ множества $\boldsymbol Z$, состоящая из чётных чисел, сама является группой относительно той же операции. В таком случае говорят, что $H$ – подгруппа группы $\boldsymbol Z$. Обе группы $\boldsymbol Z$ и $H$ удовлетворяют следующему дополнит. условию: 4) $a+b=b+a$ для любых $a$ и $b$ из группы. Всякая группа, в которой выполняется последнее условие, называется коммутативной или абелевой.
3. Множество всех подстановок (перестановок) $n$ символов образует группу относительно композиции подстановок, называемую симметрич. группой степени $n$. При $n \geq3$ симметрич. группа некоммутативна. Порядок (число элементов) симметрич. группы равен $n!$ (см. Комбинаторный анализ).
Историческая справка
Г. т. послужила во многих отношениях образцом при перестройке алгебры и математики вообще на рубеже 19–20 вв. Истоки понятия группы обнаруживаются в нескольких дисциплинах, главная из которых – теория решений алгебраич. уравнений в радикалах. В 1771 франц. математики Ж. Лагранж и А. Вандермонд впервые для нужд этой теории применили подстановки. Затем в ряде работ итал. математика П. Руффини (1799 и в последующих), посвящённых доказательству неразрешимости уравнений 5-й степени в радикалах, систематически использовалась замкнутость множества подстановок относительно их композиции и по существу описаны подгруппы группы всех подстановок пяти символов. Глубокие связи между свойствами групп подстановок и свойствами уравнений были обнаружены Н. Абелем (1824) и Э. Галуа (1830). Галуа принадлежат мн. достижения в Г. т., такие как открытие роли т. н. нормальных подгрупп в связи с задачей о разрешимости уравнений в радикалах, доказательство простоты знакопеременных групп степени $n \geq 5$; он же ввёл термин «группа», хотя и не дал его строгого определения. Важную роль в систематизации и развитии Г. т. сыграл трактат М. Э. К. Жордана о группе подстановок (1870).
Независимо (и из других соображений) понятие группы возникло в геометрии, когда в сер. 19 в. на смену античной геометрии пришли др. «геометрии» и встал вопрос об установлении связей и родства между ними. Выход из создавшегося положения был намечен исследованиями по проективной геометрии, посвящёнными изучению поведения фигур при разл. преобразованиях. Постепенно интерес в этих исследованиях перешёл на изучение самих преобразований и поиск их классификации. Таким «изучением геометрического родства» занимался А. Мёбиус. Заключит. этапом на этом пути явилась «Эрлангенская программа» Ф. Клейна (1872), положившая в основу классификации геометрий понятие группы преобразований: каждая геометрия определена некоторой группой преобразований пространства, и только те свойства фигур принадлежат данной геометрии, которые инвариантны относительно преобразований соответствующей группы.
Третий источник происхождения понятия группы – чисел теория. Л. Эйлер (1761), изучая «вычеты, остающиеся при делении степеней», по существу пользовался сравнениями и разбиениями на классы вычетов, что на теоретико-групповом языке означает разложение группы на смежные классы по подгруппе. К. Гаусс в «Арифметических исследованиях» (1801), занимаясь уравнением деления круга, фактически определил подгруппы его группы Галуа (см. Галуа теория). Там же, изучая «композицию двоичных квадратичных форм», Гаусс по существу доказал, что классы эквивалентных форм образуют конечную абелеву группу относительно композиции.
Единство теоретико-групповых форм мышления, существовавших к кон. 19 в. в разл. областях математики, привело к выработке совр. абстрактного понятия группы (С. Ли, Ф. Г. Фробениус и др.). Так, уже в 1895 Ли определял группу как совокупность преобразований, замкнутую относительно их композиции, удовлетворяющей условиям 1), 2), 3). Изучение групп без предположения их конечности и без каких бы то ни было предположений о природе элементов впервые оформилось в самостоят. раздел математики с выходом книги О. Ю. Шмидта «Абстрактная теория групп» (1916).
Основные разделы теории групп
Конечной целью собственно Г. т. является описание всех возможных групповых композиций. В Г. т. выделяется ряд разделов, определяемых чаще всего дополнит. условиями на групповую композицию или внесением в группу дополнит. структур, связанных с групповой композицией. Важнейшими в Г. т. считаются следующие разделы.
а) Теория конечных групп. Осн. проблема этой старейшей ветви Г. т. – классификация т. н. простых конечных групп, играющих роль блоков при построении произвольной конечной группы. С теорией конечных групп тесно связана комбинаторная теория групп, где используются идеи и методы комбинаторного анализа.
б) Теория абелевых групп. Отправной точкой мн. исследований в этой области служит осн. теорема о конечно порождённых абелевых группах, полностью выясняющая их строение.
в) Теория разрешимых групп. Понятие разрешимой группы является обобщением понятия абелевой группы. Оно по существу идёт от идей Э. Галуа и тесно связано с разрешимостью уравнений в радикалах. Для конечных групп это понятие может быть определено мн. равносильными способами, которые перестают быть равносильными при отказе от конечности группы. Изучение возникающих при этом классов групп составляет предмет теории обобщённо разрешимых групп.
г) Теория групп преобразований. Понятие группы возникло исторически именно как понятие группы преобразований, но в дальнейшем было обобщено, при этом Г. т. преобразований осталась важной частью общей теории. Типичным в этой теории является вопрос о том, какими свойствами обладает группа, заданная как группа преобразований некоторого множества. К Г. т. преобразований относятся, в частности, группа подстановок и группа матриц.
д) Теория представлений групп. Эта теория – одно из средств изучения абстрактных групп. Представление абстрактной группы в виде некоторой конкретной группы (напр., в виде группы подстановок или группы матриц) позволяет обнаруживать важные свойства этой группы. В теории конечных групп с помощью теории представлений получен ряд важных результатов.
е) Из разделов Г. т., выделяемых внесением в группу дополнит. структур, согласованных с групповой композицией, особенно важна теория топологич. групп, в которых групповая композиция в некотором смысле непрерывна. Старейшая ветвь этого раздела Г. т. – Ли групп теория.
Г. т. является одной из самых развитых областей алгебры и имеет многочисл. применения как в самой математике, так и в её приложениях. Напр., Е. С. Фёдоров (1890) с помощью Г. т. решил задачу классификации правильных пространственных систем точек, являющуюся одной из осн. задач кристаллографии. Это был исторически первый случай применения Г. т. непосредственно в естествознании. Большую роль Г. т. играет в физике, напр. в квантовой механике, где широко используются соображения симметрии и теория представления групп линейными преобразованиями.