ДИНАМИ́ЧЕСКАЯ СИСТЕ́МА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ДИНАМИ́ЧЕСКАЯ СИСТЕ́МА, математич. модель эволюции реальной (физической, биологической, экономической и др.) системы, состояние которой в любой момент времени однозначно определяется её начальным состоянием.
Историческая справка
Основатели теории Д. с. – А. Пуанкаре и А. М. Ляпунов. В кон. 19 – нач. 20 вв. они обнаружили и исследовали класс задач (в небесной механике, в теории фигур равновесия вращающейся жидкости и т. д.), в которых необходимо было знать поведение не одного отдельно взятого решения $х(t)$ системы обыкновенных дифференциальных уравнений (ОДУ), а всех (или очень многих) решений, соответствующих разл. начальным состояниям реальной (напр., физич.) системы. В этом случае $x(t)$ можно представить как кривую в пространстве всевозможных состояний (т. е. значений векторов $x$) и воспользоваться геометрич. свойствами этой кривой для понимания и описания свойств решения $x(t)$. Такая кривая называется фазовой траекторией.
В 1-й трети 20 в. теория Д. с. развивалась в работах ряда математиков. Наибольшее значение имели работы А. А. Андронова, который осознал и показал на важных примерах, что теория Д. с. эффективна для исследования нелинейных процессов в природе и в лаборатории. К этому времени стала понятна необходимость изучения нелинейных задач, т. к. линейный математич. аппарат часто не в состоянии описать реальные процессы. Андронов описал автоколебания с помощью предельных циклов Пуанкаре и очертил контуры новой науки – нелинейной динамики. Вместе с Л. С. Понтрягиным он ввёл понятие грубой системы, нечувствительной к малым изменениям параметров. Такая система не меняет резко свойств при малых изменениях параметров, т. е. её состояния до и после изменения параметров топологически тождественны (эквивалентны). Грубые системы заполняют открытые области в функциональном пространстве всех Д. с. Вне этих областей и, в частности, на их границах лежат негрубые системы. Проход через границу сопровождается бифуркацией – сменой структуры Д. с. В семействе Д. с., зависящих от параметра, зная структуру Д. с. при начальном значении параметра и все бифуркации, можно однозначно предсказать её структуру при конечном значении параметра.
Во 2-й пол. 20 в. Д. В. Аносов, В. И. Арнольд, Р. Боуэн, Р. Мане, Я. Г. Синай, С. Смейл, С. Хаяси, Л. П. Шильников и др. развили идеи Андронова и создали глубокую и стройную теорию Д. с., которая даёт верные представления о природе детерминистских процессов и позволяет исследовать модели реальных систем.
Характеристики динамической системы
Определение Д. с. включает в себя пространство состояний {${x}$} и зависящий от времени $t$ оператор (закон) эволюции φt, по которому система из начального состояния $x_0$ приходит в состояние $х_t$ в момент времени $t$. Состояние Д. с. описывают набором переменных $x$, выбираемых из соображений естественности их интерпретации, простоты описания, симметрии и т. п. Множество состояний (фаз) Д. с. образует фазовое пространство, в котором каждому состоянию отвечает точка, а эволюция изображается движением точки по фазовой траектории – кривой, вложенной в фазовое пространство. Напр., движение $n$ частиц под действием сил притяжения описывается в фазовом пространстве множеством всех наборов координат и скоростей этих частиц, а оператор эволюции определяется решением соответствующей системы ОДУ.
Особенности эволюции системы проявляются в типе фазовых траекторий. В частности, состоянию равновесия Д. с. соответствует вырожденная траектория – точка в фазовом пространстве, периодическому движению – замкнутая кривая, квазипериодическому движению, имеющему в спектре $m$ базовых частот, – кривая на $m$-мерном торе, вложенном в фазовое пространство. Стационарному режиму (установившемуся движению) диссипативной системы соответствует аттрактор – множество траекторий, притягивающих к себе все близкие траектории. Установившимся периодич. колебаниям соответствует предельный цикл – изолированная (в фазовом пространстве) замкнутая траектория; хаотич. автоколебаниям отвечает обычно странный аттрактор – притягивающее множество, состоящее из неустойчивых траекторий.
По характеру уравнений и методам исследований Д. с. делят на конечномерные (с конечномерным фазовым пространством) и бесконечномерные (распределённые). Конечномерные Д. с. можно подразделить на консервативные и диссипативные, что соответствует разл. физич. природе реальных систем. Консервативные Д. с. – это системы с сохраняющимся фазовым объёмом. Их образуют гамильтоновы системы с не зависящей от времени функцией Гамильтона. У диссипативных систем фазовый объём не сохраняется, в их фазовом пространстве существует ограниченная область (шар диссипации), в которую попадает навсегда точка на любой траектории.
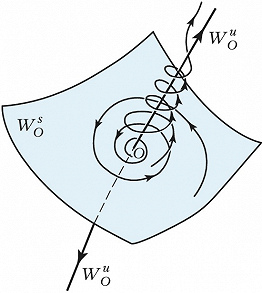
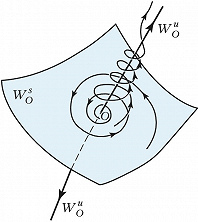
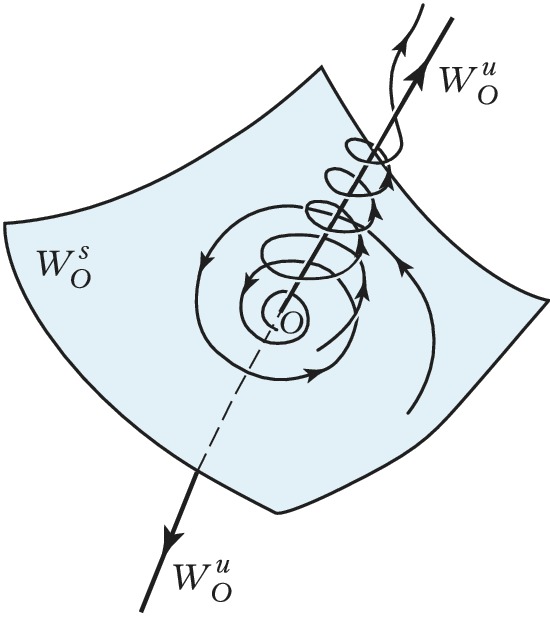
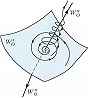
Д. с. можно также подразделить на системы с непрерывным и дискретным временем. Д. с. с непрерывным временем задаётся обычно системой ОДУ $x=f(x)$ ($x$ – скалярная либо векторная величина, точкой обозначено дифференцирование по времени), в которой для каждой начальной точки $x$ имеется единственное решение. Состояние равновесия $x_0$ такой Д. с. определяется из уравнения $f(x_0)=0$. Поведение в окрестности состояния равновесия $О$ зависит от свойств линеаризованной вблизи О системы, а именно от корней λ1, λ2, …, λn характеристич. уравнения $det[𝜕f_i/𝜕x_j-λδij]= 0$,где δij – символ Кронекера. Пусть Re λj отрицательны для р и положительны для q корней, причём p+q=n. Если р=n (q=n), точка О называется устойчивым (неустойчивым) узлом. Близкие к этой точке в фазовом пространстве траектории притягиваются к ней в случае устойчивого узла, когда время t→+$\infty$, а в случае неустойчивого узла – при t→-$\infty$. Если p≠0, q≠0, точка О называется седлом. Через неё проходят две поверхности: р-мерная и q-мерная , называемые устойчивым и неустойчивым многообразиями седла O, а также устойчивой и неустойчивой сепаратрисами. Эти поверхности образованы траекториями, стремящимися к О при t→+$\infty$ и t→-$\infty$ соответственно. Остальные траектории уходят из седла при t→±$\infty$ (рис. 1). Траектория, лежащая одновременно в $W_O^sW_O^u$ (и не совпадающая с О), называется гомоклинической или петлёй сепаратрисы седла. В одномерных моделях непрерывной среды гомоклинич. траектории отвечает стационарная бегущая волна в форме солитона.
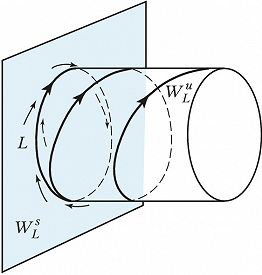
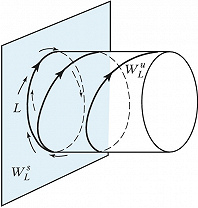
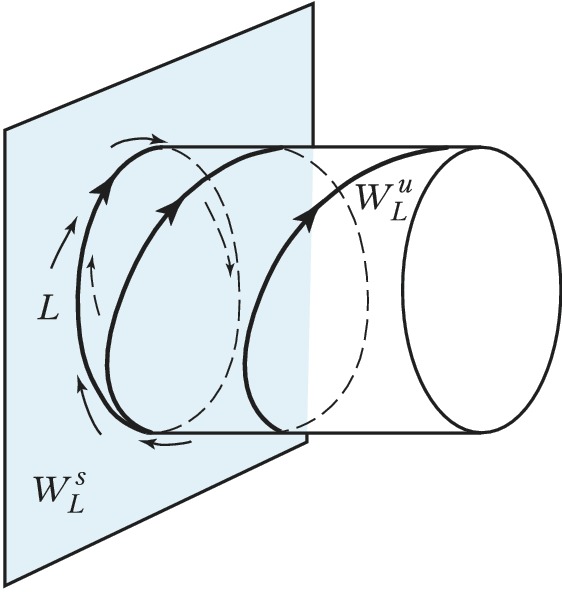
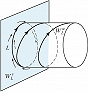
Периодич. решение $x=p(t)$ системы $x=f(x)$ имеет следующее свойство: $p(t)=p(t+T)$ для любого $t$, где $T$ – период. Этому решению соответствует замкнутая траектория $L$ в фазовом пространстве. Поведение траекторий в окрестности периодич. траектории $L$ характеризуется мультипликаторами $γ_1, …, γ_n$, которые находятся с помощью решений линеаризованной на $L$ системы. Один из них, напр. $γ_n$, всегда равен 1. Если $|\gamma_i|<1(|\gamma_i|>1)$для всех $i=1,2,...,n-1$, то траектория $L$ устойчива (неустойчива). Если $p$ мультипликаторов лежат внутри, а $q$ – вне единичного круга комплексной плоскости, $p+q=n-1$, то $L$ – траектория седлового типа. Она лежит в пересечении двух поверхностей: $p+1$-мерной $W^s_L$ и $q+1$-мерной $W_L^u$ (устойчивой и неустойчивой сепаратрис). Поверхность $W^s_L(W_L^u)$ состоит из траекторий, стремящихся к $L$ при $t→+\infty (t→-\infty)$. При $n$=3 и $p=q=1$ поверхность $W^s_L(W_L^u)$ топологически эквивалентна цилиндру, если мультипликатор $γ$ положителен и больше 1 (рис. 2).
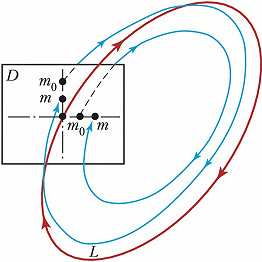
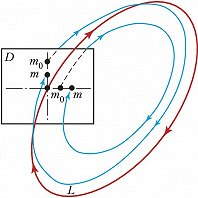
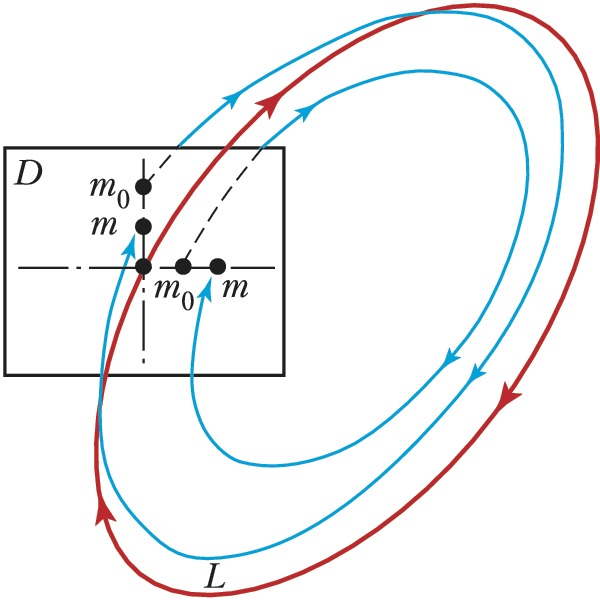
Поведение траекторий в окрестности $L$ изучают, рассматривая их следы на ($n$-1)-мерной поверхности $D$, пересекающей (без касания) $L$ и близкие к ней траектории. Если точка $m_0$ на $D$ достаточно близка к $L$, то траектория, проходящая через $m_0$, пересекает $D$ в другой точке $m$, называемой отображением последования (отображением Пуанкаре) (рис. 3). Линеаризация отображения Пуанкаре в точке пересечения $L$ с $D$ описывается матрицей Якоби. Её собственные значения $γ_1, ..., γ_{n–1}$ являются мультипликаторами замкнутой траектории $L$.
Устойчивые и неустойчивые многообразия периодич. траекторий могут пересекаться. Траектория, принадлежащая пересечению и и отличная от L, является гомоклинической. Если это пересечение происходит без касания, то в окрестности гомоклинич. траекторий имеется множество разнообразных неустойчивых траекторий, среди которых содержится бесконечное множество замкнутых траекторий седлового типа. Подобное множество траекторий типично для Д. с. с хаотич. динамикой. Т. о., наличие гомоклинич. траекторий может служить критерием существования хаотич. режимов в Д. с. (см. Динамический хаос).
Д. с. с дискретным временем обычно задаются отображением $G$ фазового пространства в себя: $x_{n+1}=G(x_n)$. Тогда эволюционный оператор $φ^t$, $t=m$, – просто $m$ раз применённое отображение $G$: $φ^nx=G(G(...G(x)...))$. Напр., простейшая модель динамики популяций описывает плотность числа членов $(n+1)$-й генерации, $x_{n+1}$, как функцию числа $х_n$ предыдущей генерации: $x_{n+1}=ax_n-bx_n^2,a,b>0$ – параметры задачи. В зависимости от значений $а$ и $b$ эта Д. с. может демонстрировать либо регулярную (все аттракторы – периодич. траектории), либо хаотич. динамику.
Отображение Пуанкаре фактически определяет систему с дискретным временем. Напр., Д. с., описывающие действие периодич. возмущения на систему ОДУ, которые можно записать в виде
$x=f(x,θ), θ=ω$, где $f$ – периодическая по $θ$ вектор-функция, всегда порождают отображение Пуанкаре. Для таких систем существует глобальная секущая поверхность Пуанкаре $θ$=0, которую каждая траектория пересекает бесконечное число раз. Поведение траекторий в системе с непрерывным временем полностью определяется Д. с. с дискретным временем.
Важная часть теории Д. с. – эргодическая теория, которая описывает статистич. свойства траекторий. Если они неустойчивы, точки на разных траекториях расходятся в процессе эволюции на существенное расстояние друг от друга, несмотря на близость начальных состояний, система демонстрирует «чувствительную зависимость» от начальных условий. (Заметим, что именно с неустойчивостью траекторий связана невозможность долгосрочного предсказания погоды.) Поскольку невозможно определить начальное состояние с бесконечной точностью (всегда существуют мельчайшие ошибки измерения или запоминания), необходимо изучать поведение не отд. траекторий, а пучков траекторий, проходящих сквозь «пятно» начальных условий. Эти траектории могут обладать разл. свойствами, и разнообразие этих свойств можно описать в терминах вероятностных распределений. А. Пуанкаре первым высказал в качественной форме мысль, что при неустойчивости траекторий Д. с. речь может идти об их статистич. свойствах такого же характера, какие к тому времени уже упоминались в работах Л. Больцмана и Дж. У. Гиббса по статистич. механике. Подобные идеи были реализованы в эргодической теории и успешно осуществляют роль «моста» между детерминированным и случайным «мирами».
С помощью теории Д. с. изучены и объяснены многие нелинейные явления в природе и технике, такие как динамический хаос, синхронизация периодич. и хаотич. колебаний, образование диссипативных структур, пространственно-временной хаос в моделях распределённых систем, конкуренция мод в нейронных сетях мозга и т. д.
-
Рис. 1. Устойчивая и неустойчивая сепаратрисы седлового состояния равновесия О. -
Рис. 2. Устойчивая и неустойчивая сепаратрисы седлового периодического движения L в случае положительных мультипликаторов. -
Рис. 3. Отображение Пуанкаре по траекториям, проходящим в окрестности седлового периодического движения.
