ДИНАМИ́ЧЕСКИЙ ХА́ОС

ДИНАМИ́ЧЕСКИЙ ХА́ОС, не­ре­гу­ляр­ное, не­пред­ска­зуе­мое из­ме­не­ние со­стоя­ния пол­но­стью де­тер­ми­ни­ро­ван­ной сис­те­мы, об­ла­даю­щее осн. свой­ст­ва­ми слу­чай­но­го про­цес­са. Ро­ж­де­ние слу­чай­но­го в не­слу­чай­ном вы­гля­дит па­ра­док­саль­ным, по­сколь­ку про­ти­во­ре­чит ин­туи­тив­ным пред­став­ле­ни­ям о том, что сис­те­ма, жи­ву­щая по про­стым пра­ви­лам, ве­дёт се­бя про­сто (т. е. ре­гу­ляр­но), а по­ве­де­ние слож­ной сис­те­мы долж­но быть слож­ным и не­пред­ска­зуе­мым.

Историческая справка и примеры систем с динамическим хаосом

Ис­поль­зуя за­ко­ны Нью­то­на, мож­но рас­счи­тать тра­ек­то­рии пла­нет Сол­неч­ной сис­те­мы не толь­ко на сто­ле­тия, но и на мил­лио­ны лет впе­рёд. Это пол­ная пред­ска­зуе­мость по­ве­де­ния ди­на­мич. сис­те­мы. Но да­же в та­кой пред­ска­зуе­мой сис­те­ме су­ще­ст­ву­ет объ­ект с не­ре­гу­ляр­ным по­ве­де­ни­ем – это спут­ник Са­тур­на Ги­пе­рон. Его дви­же­ние так­же удов­ле­тво­ря­ет за­ко­нам ди­на­ми­ки, од­на­ко его тра­ек­то­рия в про­стран­ст­ве хао­ти­че­ски вьёт­ся в ок­ре­ст­но­сти сред­ней ор­би­ты. Это не един­ст­вен­ный при­мер для ди­на­ми­ки пла­нет. Хао­ти­че­ским мог­ло бы быть и дви­же­ние Зем­ли в гра­ви­та­ци­он­ном по­ле двух солнц.

Рис. 1. Случайное блуждание шарика в бильярде Синая (близкие в начальный момент траектории расходятся).

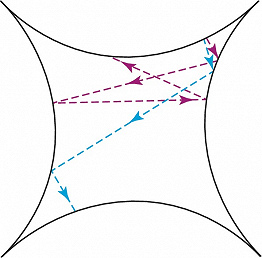
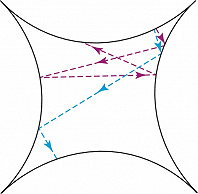
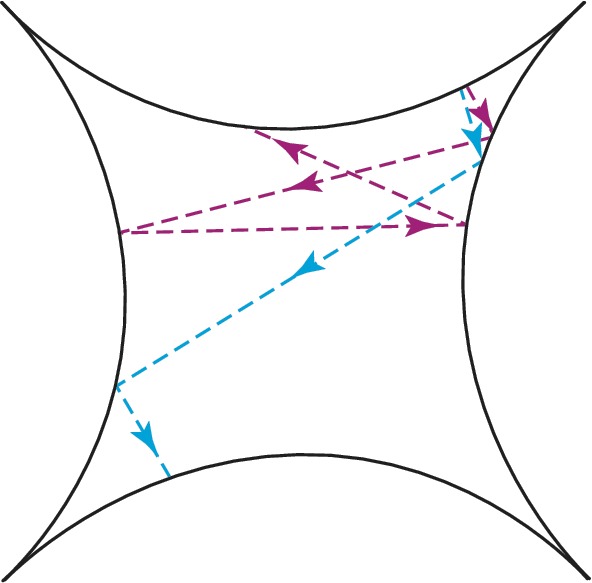
На пер­вый взгляд, нет бо­лее пред­сказуе­мо­го по­ве­де­ния, чем дви­же­ние оди­но­ко­го ша­ра на бильярд­ном сто­ле. Од­на­ко ес­ли стен­ки бильяр­да во­гну­тые (бильярд Си­ная), то дви­же­ние ша­ра непред­ска­зуе­мо. При­чи­на этой не­пред­ска­зуе­мо­сти за­клю­ча­ет­ся в экс­по­нен­ци­аль­ной не­ус­той­чи­во­сти ин­ди­ви­ду­аль­ных тра­ек­то­рий, ко­то­рая при­во­дит к чув­ст­ви­тель­ной за­ви­си­мо­сти от на­чаль­ных ус­ло­вий (рис. 1). Та­кая чув­ст­ви­тель­ная за­ви­си­мость – осн. чер­та всех сис­тем с ди­на­мич. хао­сом.

Рис. 2. Водяное колесо способно хаотически менять направление вращения.

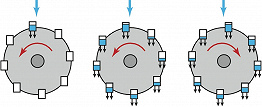
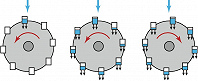
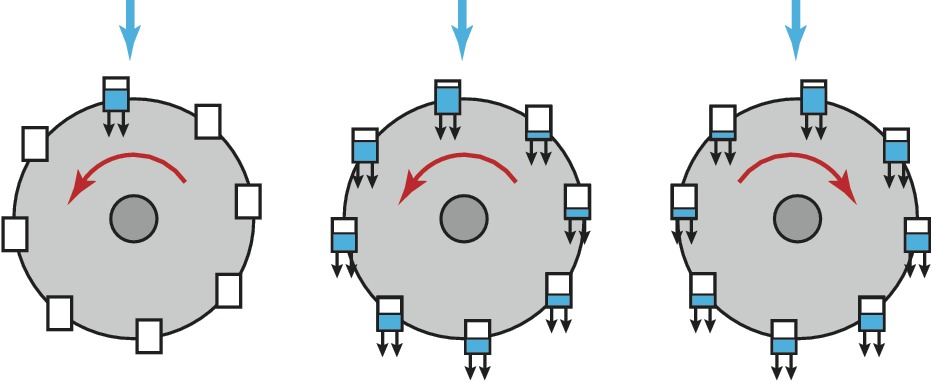
На рис. 2 пред­став­ле­но «чёр­то­во ко­ле­со», где в ка­че­ст­ве пас­са­жи­ров рас­по­ло­же­ны ча­ши, за­пол­няе­мые свер­ху во­дой. Пусть ко­ле­со вра­ща­ет­ся про­тив часо­вой стрел­ки. Ес­ли по­ток во­ды дос­та­точ­но силь­ный, ко­ле­со на­чи­на­ет вра­щать­ся бы­ст­рее и под­ни­маю­щие­ся на­верх ча­ши про­ска­ки­ва­ют верх­нюю точ­ку, не ус­пев за­пол­нить­ся. Ко­гда ле­вое пле­чо ко­ле­са ста­нет на­столь­ко лег­че пра­во­го, что сил инер­ции не хва­тит, что­бы про­дол­жить вра­ще­ние, ко­ле­со на мгно­ве­ние ос­та­но­вит­ся и за­тем вновь нач­нёт вра­щать­ся, но уже в про­ти­во­по­лож­ную сто­ро­ну. Та­кой про­цесс мо­жет быть как пе­рио­ди­че­ским, так и хао­ти­че­ским. Ма­те­ма­ти­че­ски та­кое вра­ще­ние ко­ле­са опи­сы­ва­ет­ся так же, как и кон­век­тив­ное дви­же­ние в слое жид­ко­сти, по­дог­ре­вае­мом сни­зу (мо­дель Ло­рен­ца). По­ве­де­ние та­кой сис­те­мы мож­но пред­ска­зать толь­ко на ко­рот­кое вре­мя.

Рис. 3. Фазовый портрет капли молока, закрученной ложечкой в чашке кофе.

При­мер не­ре­гу­ляр­но­го по­ве­де­ния час­тиц в ре­гу­ляр­ном пе­рио­дич. по­ле ско­ро­стей – хао­тич. пе­ре­ме­ши­ва­ние (ка­п­ля мо­ло­ка в чаш­ке ко­фе, за­кру­чен­ная ло­жеч­кой, рис. 3). По­доб­ное пе­ре­ме­ши­ва­ние пред­став­ля­ет со­бой це­поч­ку че­ре­дую­щих­ся рас­тя­же­ний и скла­ды­ва­ний ка­п­ли.

До 19 в. Все­лен­ная рас­смат­ри­ва­лась как пред­ска­зуе­мая сис­те­ма. П. Ла­п­лас пред­по­ла­гал, что eё со­стоя­ния мо­гут быть вы­чис­ле­ны, ес­ли все си­лы, дей­ст­вую­щие в при­ро­де, за­да­ны и на­чаль­ные ус­ло­вия для всех не­бес­ных тел из­вест­ны (ла­п­ла­сов­ский де­тер­ми­низм). Од­на­ко в кон. 19 в. А. Пу­ан­ка­ре от­крыл, что дви­же­ние не­бес­ных тел не яв­ля­ет­ся пол­но­стью пред­ска­зуе­мым – гра­ви­та­ци­он­ное взаи­мо­дей­ст­вие бо­лее чем двух не­бес­ных тел опи­сы­ва­ет­ся не­ин­тег­ри­руе­мы­ми урав­не­ния­ми с не­ус­той­чи­вы­ми и, воз­мож­но, хао­тич. тра­ек­то­рия­ми. В ла­бо­ра­то­рии слож­ное по­ве­де­ние срав­ни­тель­но про­стых ко­ле­ба­тель­ных сис­тем на­блю­да­лось ещё в 1920-х гг. Экс­пе­ри­мен­ты с элек­трон­ны­ми ге­не­ра­то­ра­ми и мо­де­лью маг­нит­но­го ди­на­мо (1958) по­ка­за­ли слож­ное по­ве­де­ние про­стых де­тер­ми­ни­ро­ван­ных (не­слу­чай­ных) сис­тем, од­на­ко то, что они мо­гут вес­ти се­бя хао­ти­че­ски, ещё не бы­ло осоз­на­но. Толь­ко в нач. 1960-х гг. ре­зуль­та­ты ком­пь­ю­тер­но­го мо­де­ли­ро­ва­ния (Э. Ло­ренц, США, 1963) и ряд от­кры­тий в ма­те­ма­ти­ке при­ве­ли к ре­во­лю­ции в по­ни­ма­нии при­ро­ды слу­чай­но­го, а к кон. 20 в. по­ня­тие Д. х. стало ре­аль­ным и при­выч­ным.

Характеристики хаоса

Су­ще­ст­во­ва­ние Д. х., ко­то­рый при­сущ мно­гим ди­на­ми­чес­ким сис­те­мам, свя­за­но с т. н. ло­каль­ной не­ус­той­чи­во­стью тра­ек­то­рий. В про­стран­ст­ве, об­ра­зо­ван­ном мно­же­ст­вом все­воз­мож­ных со­стоя­ний сис­те­мы (фа­зо­вом про­стран­ст­ве), ло­каль­ная ус­той­чи­вость вы­бран­ной тра­ек­то­рии оп­ре­де­ля­ет­ся зна­ком по­ка­за­те­лей Ля­пу­но­ва, ко­то­рые вы­чис­ля­ют­ся как сред­нее по вре­ме­ни от ло­га­риф­ма от­но­ше­ния раз­ме­ра ка­п­ли фа­зо­вой жид­ко­сти, дви­жу­щей­ся вдоль тра­ек­то­рии, в мо­мент вре­ме­ни t к её раз­ме­ру в на­чаль­ный мо­мент вре­ме­ни. Чис­ло по­ка­за­те­лей Ля­пу­но­ва рав­но раз­мер­но­сти фа­зо­во­го про­стран­ст­ва. Вдоль од­них на­прав­ле­ний близ­кие тра­ек­то­рии мо­гут экс­по­нен­ци­аль­но рас­хо­дить­ся (не­ус­той­чи­вые на­прав­ле­ния), а вдоль дру­гих, на­обо­рот, мо­гут при­бли­жать­ся друг к дру­гу. От­ве­чаю­щие им по­ка­за­те­ли со­от­вет­ст­вен­но по­ло­жи­тель­ны и от­ри­ца­тель­ны. Сум­ма по­ло­жи­тель­ных по­ка­за­те­лей Ля­пу­но­ва, ха­рак­те­ри­зую­щая не­ус­той­чи­вость рас­смат­ри­вае­мой тра­ек­то­рии, боль­ше или рав­на эн­тро­пии Кол­мо­го­ро­ва – Си­ная. Вви­ду рас­хо­ди­мо­сти близ­ких тра­ек­то­рий в фа­зо­вом про­стран­ст­ве бо­лее дли­тель­ное на­блю­де­ние хао­тич. тра­ек­то­рии да­ёт бо­лее де­таль­ную ин­фор­ма­цию о на­чаль­ных ус­ло­ви­ях: хао­тич. тра­ек­то­рия по­ро­ж­да­ет ин­фор­ма­цию. Ве­ли­чи­на этой ин­фор­ма­ции с об­рат­ным зна­ком рав­на эн­тро­пии Кол­мо­го­ро­ва – Си­ная. Д. х. – это по­ве­де­ние ди­на­мич. сис­те­мы, ха­рак­те­ри­зуе­мое ко­неч­ной по­ло­жи­тель­ной эн­тро­пи­ей Кол­мо­го­ро­ва – Си­ная. Пред­став­лен­ный на рис. 3 фа­зо­вый порт­рет (со­во­куп­ность тра­ек­то­рий в фа­зо­вом про­стран­ст­ве) от­ра­жа­ет на­ли­чие по­ряд­ка в Д. х., его под­чи­не­ние срав­ни­тель­но про­стым за­ко­нам. На хао­тич. мно­же­ст­ве пе­ре­ме­ши­ваю­щий­ся фа­зо­вый по­ток хра­нит па­мять о по­сле­до­ва­тель­ных рас­тя­же­ни­ях и скла­ды­ва­ни­ях.

Хао­тич. мно­же­ст­ва га­миль­то­но­вых сис­тем, а так­же стран­ные ат­трак­то­ры сис­тем с дис­си­па­ци­ей не за­пол­ня­ют пол­но­стью к.-л. объ­ём в фа­зо­вом про­стран­ст­ве. Это мно­же­ст­ва с дроб­ной раз­мер­но­стью, или фрак­та­лы. Час­то та­кие мно­же­ст­ва са­мо­по­доб­ны. Хао­тич. тра­ек­то­рию мож­но рас­смат­ри­вать как на­бор от­рез­ков бес­ко­неч­но­го чис­ла разл. пе­рио­дич. тра­ек­то­рий, от­ра­жаю­щих су­ще­ст­во­ва­ние в хао­тич. мно­же­ст­ве бес­ко­неч­но­го чис­ла не­ус­той­чи­вых цик­лов.

Маломерный хаос и турбулентность

Сце­на­рии ро­ж­де­ния ма­ло­мер­но­го Д. х., т. е. по­сле­до­ва­тель­но­сти би­фур­ка­ций, пред­ше­ст­вую­щих его воз­ник­но­ве­нию, яв­ля­ют­ся об­щи­ми для сис­тем разл. при­ро­ды. Их ана­лиз по­зво­лил, в ча­ст­но­сти, при­бли­зить­ся к по­ни­ма­нию ди­на­мич. при­ро­ды воз­ник­но­ве­ния тур­бу­лент­но­сти при по­те­ре ус­той­чи­во­сти ла­ми­нар­ным те­че­ни­ем. Экс­пе­ри­мен­ты с за­кры­ты­ми те­че­ния­ми про­де­мон­ст­ри­ро­ва­ли неск. уни­вер­саль­ных сце­на­ри­ев за­ро­ж­де­ния слу­чай­но­го: 1) це­поч­ка би­фур­ка­ций уд­вое­ния пе­рио­да в кон­век­тив­ных ячей­ках Рэ­лея – Бе­на­ра; 2) пе­ре­ход к хао­су че­рез раз­ру­ше­ние ква­зи­пе­рио­дич. те­че­ний; 3) пе­ре­ход че­рез пе­ре­ме­жае­мость, т. е. ро­ж­де­ние ло­ка­ли­зо­ван­ных хао­тич. вспле­сков. Об­на­ру­же­ние этих сце­на­ри­ев под­твер­ди­ло идею о ди­на­мич. при­ро­де пе­ре­хо­да к тур­бу­лент­но­сти.