ПРЕДЕ́ЛЬНЫЙ ЦИКЛ

Рис. 1. Устойчивый предельный цикл на плоскости (а) и соответствующие ему периодические автоколебания (б).

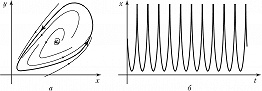
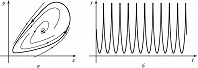
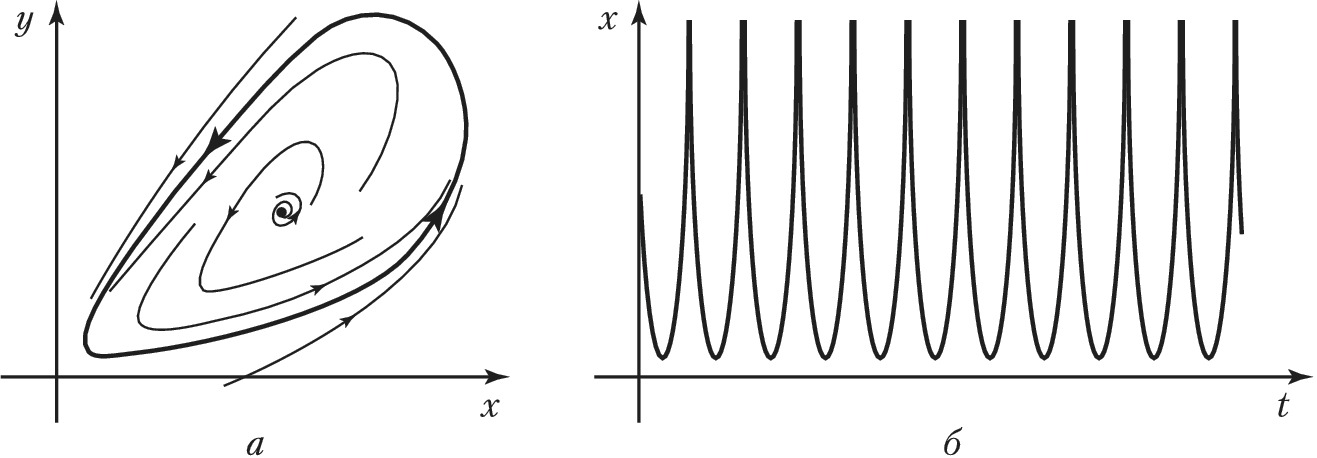
ПРЕДЕ́ЛЬНЫЙ ЦИКЛ, изо­ли­ро­ван­ная за­мк­ну­тая тра­ек­то­рия ди­на­мич. сис­те­мы (за­дан­ной не­ли­ней­ной сис­те­мой обык­но­вен­ных диф­фе­рен­ци­аль­ных урав­не­ний) в фа­зо­вом про­стран­ст­ве, изо­бра­жаю­щая пе­рио­дич. дви­же­ние. П. ц. мо­жет быть гру­бым (струк­тур­но ус­той­чи­вым) и не­гру­бым. Не­гру­бый П. ц. ис­че­за­ет в фа­зо­вом про­стран­ст­ве при сколь угод­но ма­лых из­ме­не­ни­ях па­ра­мет­ров ди­на­ми­че­ской сис­те­мы, а гру­бый – со­хра­ня­ет­ся да­же при из­ме­не­ни­ях па­ра­мет­ров в ко­неч­ных пре­де­лах. П. ц. яв­ля­ет­ся ор­би­таль­но асим­пто­ти­че­ски ус­той­чи­вым (да­лее про­сто ус­той­чи­вым), ес­ли все тра­ек­то­рии, на­чи­наю­щие­ся в его ма­лой ок­ре­ст­но­сти, при­бли­жа­ют­ся к не­му при вре­ме­ни $t→+∞$. Ес­ли же хо­тя бы од­на из тра­ек­то­рий ухо­дит из этой ок­ре­ст­но­сти, то П. ц. не­ус­той­чив. Ус­той­чи­вый П. ц. (рис. 1, а) яв­ля­ет­ся ма­те­ма­тич. об­ра­зом в фа­зо­вом про­стран­ст­ве ус­той­чи­вых пе­рио­дич. ав­то­ко­ле­ба­ний (рис. 1, б).

Рис. 2. Седловой предельный цикл и фрагмент его инвариантных многообразий.

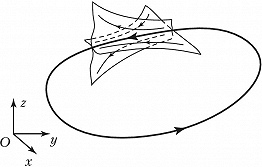
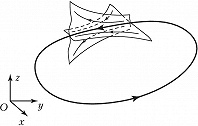
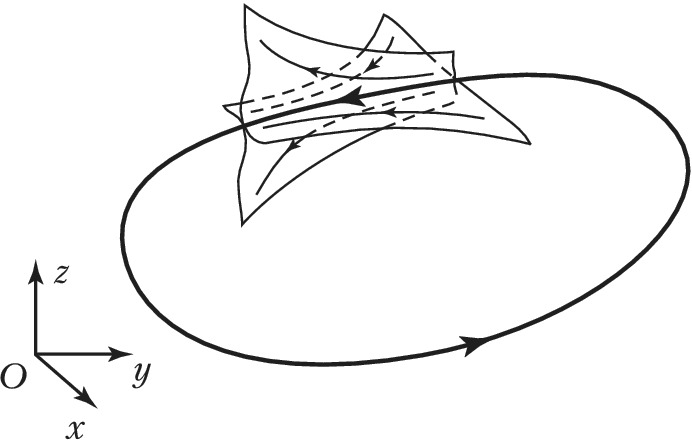
Тра­ек­то­рии, на­чи­наю­щие­ся в ма­лой ок­ре­ст­но­сти гру­бо­го не­ус­той­чи­во­го цик­ла, мо­гут по­ки­дать её по-раз­но­му: ли­бо все, ли­бо часть из них. В пер­вом слу­чае П. ц. на­зы­ва­ют про­сто не­ус­той­чи­вым, а во вто­ром – сед­ло­вым. Сед­ло­вой П. ц. од­но­вре­мен­но при­над­ле­жит как ус­той­чи­во­му ин­ва­ри­ант­но­му мно­го­об­ра­зию, по ко­то­ро­му тра­ек­то­рии асим­пто­ти­че­ски при­бли­жа­ют­ся к не­му, так и к не­ус­той­чи­во­му ин­ва­ри­ант­но­му мно­го­об­ра­зию, по ко­то­ро­му тра­ек­то­рии уда­ля­ют­ся от не­го (рис. 2). По­ня­тие сед­ло­во­го пре­дель­но­го цик­ла яв­ля­ет­ся ба­зо­вым в тео­рии ди­на­мич. хао­са.