ЦЕ́ЛЫЙ ТОН

ЦЕ́ЛЫЙ ТОН, му­зы­каль­ный ин­тер­вал. Ис­клю­чи­тель­ное по­ло­же­ние Ц. т. (час­то со­кра­щён­но «тон») в ев­роп. тео­рии му­зы­ки в том, что он ис­поль­зу­ет­ся как ме­ра для про­чих муз. ин­тер­ва­лов (по­лу­тон; чет­вер­ти­тон; три­тон; ди­тон, или боль­шая тер­ция, и др.). Ц. т. как ка­те­го­рия муз. ло­ги­ки не име­ет стро­го оп­ре­де­лён­ной ма­те­ма­тич. и аку­стич. ве­ли­чи­ны. По­след­няя ус­та­нав­ли­ва­ет­ся в за­ви­си­мо­сти от кон­крет­но­го строя му­зы­каль­но­го. В пи­фа­го­ро­вом строе Ц. т. вы­ра­жа­ет­ся от­но­ше­ни­ем 9:8. В чис­том строе раз­ли­ча­ют­ся боль­шой Ц. т. (9:8) и ма­лый Ц. т. (10:9). В рав­но­мер­но-тем­пе­ри­ро­ван­ном строе (см. Тем­пе­ра­ция) Ц. т. выра­жа­ет­ся от­но­ше­ни­ем $\sqrt[6]{2}:1$.

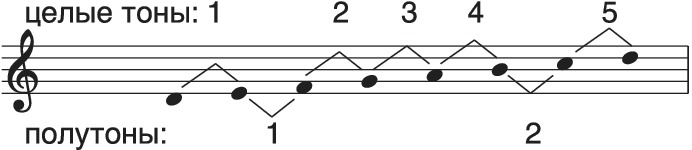
Ц. т. ис­поль­зу­ет­ся в тео­ре­тич. опи­са­ни­ях зву­ко­ря­дов то­го или ино­го ла­да, ин­тер­валь­но­го ро­да. Напр., в диа­то­нич. ок­тав­ном зву­ко­ря­де 5 Ц. т. и 2 по­лу­то­на. Ве­ли­чи­на Ц. т. d-e (в нот­ном при­ме­ре в верх­ней строч­ке ц. 1) мо­жет быть рав­на 203,9 цен­та (в пи­фа­го­ро­вом строе) или 200 цен­тов (в рав­но­мер­но-тем­пе­ри­ро­ван­ном строе); в др. стро­ях (напр., в от­тен­ках диа­то­ни­ки ма­ка­ма, му­га­ма) встре­ча­ют­ся и др. ве­ли­чи­ны. Во всех слу­ча­ях на­строй­ки диа­то­нич. гам­мы по от­но­ше­нию к это­му ин­тер­ва­лу ев­роп. тео­рия му­зы­ки ис­поль­зу­ет один и тот же тер­мин – «це­лый тон».

Ве­ли­чи­на Ц. т. и его час­тей – важ­ная про­бле­ма всей ев­роп. ис­то­рии му­зы­ки и муз. нау­ки. В ан­тич­но­сти пи­фа­го­рей­ская тра­ди­ция (напр., у Ни­ко­ма­ха и Бо­эция) предъ­яв­ля­ла ма­те­ма­ти­че­ски обос­но­ван­ные до­ка­за­тель­ст­ва не­де­ли­мо­сти Ц. т. на 2 рав­ные час­ти (в ра­цио­наль­ных чис­лах), вы­де­ляя ма­лый (лим­му) и боль­шой (апо­то­му) по­лу­то­ны. Эти до­ка­за­тель­ст­ва впо­след­ст­вии вос­про­из­во­ди­ли (с не­боль­ши­ми ва­риа­ция­ми) мно­гие ср.-век. и ре­нес­санс­ные тео­ре­ти­ки му­зы­ки, при­дер­жи­вав­шие­ся пи­фа­го­рей­ской (бо­эцие­вой) тра­ди­ции (Хук­бальд Сент-Аман­ский, Ие­ро­ним Мо­рав­ский, Якоб Льеж­ский, Про­сдо­чи­мо де Бель­до­ман­ди, Ф. Га­фу­ри и др.). Ари­сто­ксен, в про­ти­во­вес пи­фа­го­рей­цам, де­лил тон на 2 рав­ных по­лу­то­на «му­зы­каль­но», не счи­тая не­об­хо­ди­мым под­кре­п­лять своё эм­пи­рич. де­ле­ние к.-л. стро­ги­ми до­ка­за­тель­ст­ва­ми; та­кой же точ­ки зре­ния при­дер­жи­ва­лись по­сле­до­ва­те­ли его шко­лы (к «ари­сток­се­ни­кам» но­вой Ев­ро­пы от­но­сит­ся, напр., Мар­кет­то Па­ду­ан­ский, де­лив­ший Ц. т. на 5 час­тей). Про­бле­ма не ут­ра­ти­ла сво­ей ост­ро­ты и с раз­ра­бот­кой чис­то­го и сред­не­то­но­во­го стро­ёв в 15–17 вв.: чис­ло не­рав­ных по­лу­то­нов ещё боль­ше воз­рос­ло. Лишь с ус­та­нов­ле­ни­ем в 18 в. рав­но­мер­ной тем­пе­ра­ции эта про­бле­ма ис­чез­ла, но со 2-й пол. 20 в. вновь при­об­ре­ла ак­ту­аль­ность в свя­зи с ин­те­гра­ци­ей в совр. куль­ту­ру ста­рин­ной ев­роп. му­зы­ки (осо­бен­но ин­ст­ру­мен­таль­ной; см. Ау­тен­тич­ное ис­пол­ни­тель­ст­во), а так­же тра­диц. му­зы­ки Вос­то­ка.