НЕЛИНЕ́ЙНАЯ О́ПТИКА

НЕЛИНЕ́ЙНАЯ О́ПТИКА, раз­дел оп­ти­ки, свя­зан­ный с изу­че­ни­ем и при­ме­не­ни­ем яв­ле­ний, в ко­то­рых от­клик ве­ще­ст­ва на при­ло­жен­ное элек­тро­маг­нит­ное по­ле яв­ля­ет­ся не­ли­ней­ной функ­ци­ей по­ля.

Ис­то­ри­че­ская справ­ка. Пер­вые эф­фек­ты, ко­то­рые мож­но от­не­сти к Н. о., бы­ли от­кры­ты ещё в 19 в. Это Фа­ра­дея эф­фек­ты (1845) – вра­ще­ние плос­ко­сти по­ля­ри­за­ции све­то­вой вол­ны при её рас­про­стра­не­нии вдоль на­прав­ле­ния дей­ст­вую­ще­го на сре­ду маг­нит­но­го по­ля; Кер­ра эф­фек­ты – элек­тро­оп­ти­че­ский (воз­ник­но­ве­ние в оп­ти­че­ски изо­троп­ных веще­ст­вах двой­но­го лу­че­пре­лом­ле­ния, квад­ра­тич­но­го по на­пря­жён­но­сти при­ло­жен­но­го элек­трич. по­ля, 1875) и маг­ни­то­оп­ти­че­ский (влия­ние на­маг­ни­чен­но­сти сре­ды на ин­тен­сив­ность и по­ля­ри­за­цию све­та, от­ра­жён­но­го от её по­верх­но­сти, 1876). Эти эф­фек­ты свя­за­ны с влия­ни­ем элек­трич. и маг­нит­но­го по­лей на ди­элек­трич. про­ни­цае­мость сре­ды. В 1894 нем. фи­зик Ф. Пок­кельс об­на­ру­жил ли­ней­ный элек­тро­оп­тич. эф­фект (Пок­кель­са эф­фект), обу­слов­лен­ный из­ме­не­ни­ем по­ка­за­те­ля пре­лом­ле­ния сре­ды, про­пор­цио­наль­ным на­пря­жён­но­сти при­ло­жен­но­го по­сто­ян­но­го элек­трич. по­ля.

Ис­то­ки совр. Н. о. от­но­сят­ся к «до­ла­зер­ным» вре­ме­нам. Так, в 1923 рос. фи­зики С. И. Ва­ви­лов и В. Л. Лёв­шин об­на­ру­жи­ли слабое на­ру­ше­ние за­ко­на Бу­ге­ра при ис­поль­зо­ва­нии ин­тен­сив­ных све­то­вых по­то­ков, про­хо­дя­щих че­рез сре­ду, об­ла­даю­щую яр­ко вы­ра­жен­ным ме­та­ста­биль­ным уров­нем энер­гии. Позд­нее бы­ла заре­ги­ст­ри­ро­ва­на не­боль­шая не­ли­ней­ность де­по­ля­ри­за­ции лю­ми­нес­цен­ции, а так­же ин­ду­ци­ро­ван­ный из­лу­че­ни­ем ди­х­ро­изм по­гло­ще­ния. Эти эф­фек­ты свя­за­ны с пе­ре­рас­пре­де­ле­ни­ем на­се­лён­но­стей кван­то­вых уров­ней ве­ще­ст­ва под дей­ст­ви­ем до­ста­точ­но ин­тен­сив­но­го оп­тич. из­лу­че­ния.

В 1930 М. Гёп­перт-Май­ер по­ка­за­ла воз­мож­ность пе­ре­хо­да ме­ж­ду дву­мя кван­то­вы­ми уров­ня­ми при по­гло­ще­нии двух фо­то­нов. Так бы­ло пред­ска­за­но двух­фо­тон­ное, а сле­до­ва­тель­но, не­ли­ней­ное по­гло­ще­ние све­та. В 1930-х гг. Г. Пла­че­к пред­ска­зал эф­фект вы­ну­ж­ден­но­го ком­би­на­ци­он­но­го рас­сея­ния све­та. Боль­шое вни­ма­ние по­ис­ку не­ли­ней­ных оп­тич. яв­ле­ний уде­лял в 1930–40-х гг. С. И. Ва­ви­лов. Имен­но он ввёл тер­мин «Н. о.». Од­на­ко все эти идеи и пред­ска­за­ния име­ли лишь тео­ре­тич. зна­че­ние, по­сколь­ку для на­блю­де­ния не­ли­ней­ных эф­фек­тов нуж­ны ис­точ­ни­ки мощ­но­го све­то­во­го из­лу­че­ния, ко­то­рых то­гда не бы­ло.

Бур­ное раз­ви­тие Н. о. на­ча­лось по­сле соз­да­ния в 1960 пер­вых ла­зе­ров – ис­точ­ни­ков мощ­но­го ко­ге­рент­но­го све­то­во­го из­лу­че­ния. Так, в 1961 П. Фран­кен с со­труд­ни­ка­ми (США) за­ре­ги­стри­ро­ва­л эф­фект ге­не­ра­ции 2-й гар­мо­ни­ки из­лу­че­ния ру­би­но­во­го ла­зе­ра в кри­стал­ле квар­ца, а В. Кай­зер и Ч. Гар­рет (Гер­ма­ния) экс­пе­ри­мен­таль­но на­блю­да­ли двух­фо­тон­ное по­гло­ще­ние све­та. Прин­ци­пи­аль­ным для Н. о. бы­ло соз­да­ние ла­зе­ров с мо­ду­ли­ро­ван­ной доб­рот­но­стью (1962), ко­то­рые по­зво­ли­ли по­лу­чать ин­тен­сив­но­сти из­лу­че­ния по­ряд­ка 10⁹–10¹¹ Вт/см² при дли­тель­но­сти им­пуль­сов по­ряд­ка 10^–7–10^–8 с. С по­мо­щью та­ких ла­зе­ров впер­вые на­блю­да­лось вы­ну­ж­ден­ное ком­би­на­ци­он­ное рас­сея­ние све­та (1962), бы­ли по­лу­че­ны 3-я и 4-я оп­тич. гар­мо­ни­ки (1963–64) и от­кры­то вы­ну­ж­ден­ное рас­сея­ние Ман­дель­шта­ма – Брил­лю­эна (1964–65). В 1965 впер­вые на­блю­да­лась са­мо­фо­ку­си­ров­ка све­та: в не­ли­ней­ной сре­де ока­зы­ва­ет­ся воз­мож­ным по­дав­ле­ние ди­фрак­ци­он­ной рас­хо­ди­мо­сти мощ­ных све­то­вых пуч­ков за счёт не­ли­ней­ной ре­фрак­ции, ко­то­рая обу­слов­ле­на не­ли­ней­ной до­бав­кой к по­ка­за­те­лю пре­лом­ле­ния. В том же го­ду соз­дан пер­вый па­ра­мет­ри­че­ский ге­не­ра­тор све­та (ПГС), идея ко­то­ро­го бы­ла пред­ло­же­на в 1962 (С. А. Ах­ма­нов и Р. В. Хох­лов, Н. Кролл, Р. Кинг­стон). В ПГС взаи­мо­дей­ст­вие све­то­вых волн в сре­дах с квад­ра­тич­ной не­ли­ней­но­стью вос­при­им­чи­во­сти ис­поль­зу­ет­ся для ге­не­ра­ции мощ­но­го ко­ге­рент­но­го све­то­во­го из­лу­че­ния, плав­но пе­ре­страи­вае­мо­го по час­то­те. ПГС вме­сте с ла­зе­ра­ми на кра­си­те­лях ста­ли ба­зой для ис­сле­до­ва­ний час­тот­ной за­ви­си­мо­сти не­ли­ней­ных взаи­мо­дей­ст­вий и, в ча­ст­но­сти, для раз­ра­бот­ки ме­то­дов не­ли­ней­ной спек­тро­ско­пии.

С 1967 на­ча­лись ак­тив­ные ис­сле­до­ва­ния не­ста­цио­нар­ных не­ли­ней­ных про­цес­сов, т. к. поя­ви­лись ла­зе­ры, ге­не­ри­рую­щие сверх­ко­рот­кие им­пуль­сы с пи­ко­се­кунд­ной дли­тель­но­стью: $τ_и∼10^{–11}– 10^{–12}$ с. В по­ле та­ких им­пуль­сов про­явля­ет­ся не­ста­цио­нар­ность, свя­зан­ная с инер­ци­он­но­стью не­ли­ней­но­го от­кли­ка, и вол­но­вая не­ста­цио­нар­ность, обу­слов­лен­ная раз­ли­чи­ем груп­по­вых ско­ро­стей взаи­мо­дей­ст­вую­щих волн. Бы­ли про­де­мон­ст­ри­ро­ва­ны ме­то­ды не­ли­ней­но-оп­тич. фор­ми­ро­ва­ния и сжа­тия сверх­ко­рот­ких им­пуль­сов, за­пу­ще­ны пе­ре­страи­вае­мые по час­то­те ПГС пи­ко­се­кунд­ных им­пуль­сов, пе­ре­кры­ваю­щие ви­ди­мый и инфра­красный диа­па­зо­ны спек­тра. Т. о., по­яви­лась воз­мож­ность экс­пе­рим. изу­че­ния не­ста­цио­нар­ных ре­зо­нанс­ных про­цес­сов взаи­мо­дей­ст­вия, тре­бую­щих тон­кой пе­ре­строй­ки час­то­ты в пре­де­лах од­но- и мно­го­фо­тон­но­го ре­зо­нан­сов из­лу­че­ния с кван­то­вы­ми пе­ре­хо­да­ми в ве­ще­ст­ве.

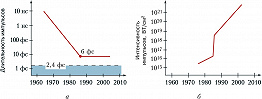
В 1980-х гг. на­ча­лось бы­строе ос­вое­ние фем­то­се­кунд­но­го диа­па­зо­на дли­тель­но­стей им­пуль­сов. К 1987 со­кра­ще­ние вре­менны́х мас­шта­бов в оп­тич. диа­па­зо­не поч­ти дос­тиг­ло пре­де­ла: бы­ли по­лу­че­ны им­пуль­сы дли­тель­но­стью $τ_и≈6$ фс в ви­ди­мом диа­па­зо­не (все­го 3 пе­рио­да све­то­вых ко­ле­ба­ний) и $τ_и≈ 40$ фс на дли­не вол­ны из­лу­че­ния $\ce{CO2}$-ла­зе­ра – све­то­вой им­пульс в один пе­ри­од ко­ле­ба­ний.

Рис. 1. Достигнутые в эксперименте предельные длительности (а) и интенсивности (б) световых импульсов в зависимости от года.

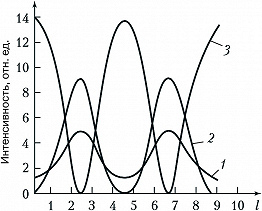
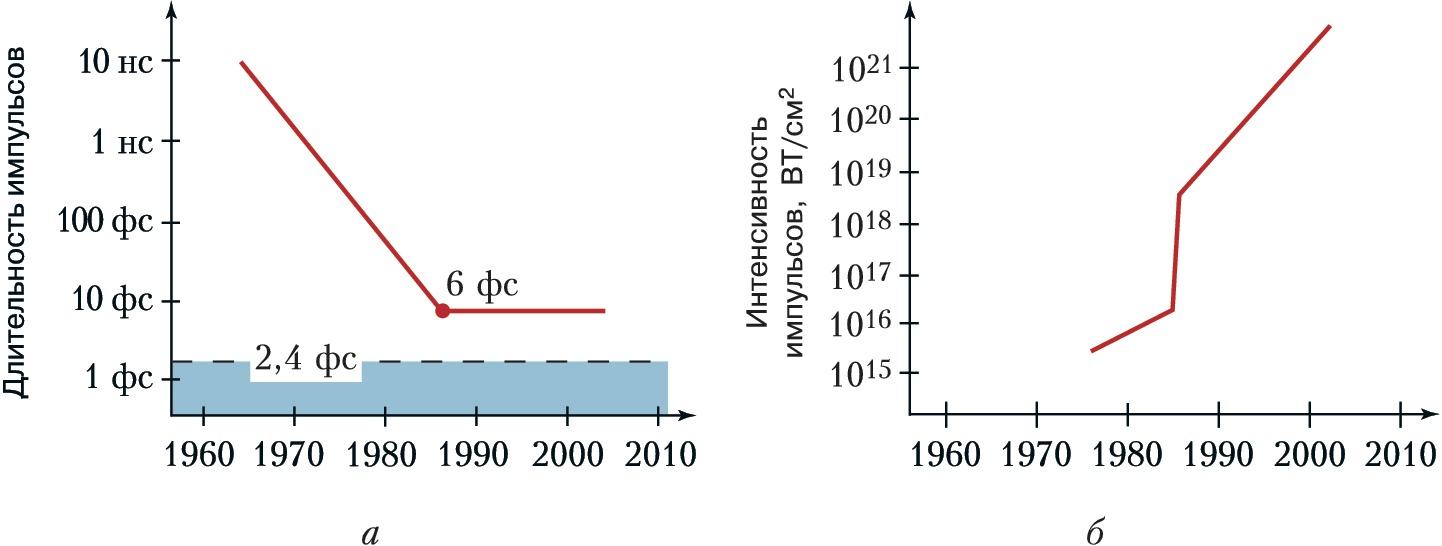
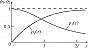
Умень­ше­ние дли­тель­но­сти оп­тич. им­пуль­сов со­про­во­ж­да­лось рос­том их пре­дель­ной ин­тен­сив­но­сти, дос­ти­жи­мой в ус­ло­ви­ях ис­сле­до­ват. ла­бо­ра­то­рий. Ди­на­ми­ка дос­ти­же­ния в разл. го­ды пре­дель­ных дли­тель­но­стей све­то­вых им­пуль­сов изо­бра­же­на на рис. 1, а. На рис. 1, б – ана­ло­гич­ная за­ви­си­мость для дос­тиг­ну­тых ин­тен­сив­но­стей им­пуль­сов. Вид­но, что уже с сер. 1980-х гг. поя­ви­лись ге­не­ра­то­ры све­то­вых им­пуль­сов с ин­тен­сив­но­стью, ко­то­рая бо­лее чем на 5 по­ряд­ков пре­вос­хо­дит ин­тен­сив­но­сти, при ко­то­рых на­пря­жён­ность све­то­во­го по­ля со­из­ме­ри­ма с на­пря­жён­но­стью внут­ри­атом­ных по­лей $E_а∼10^9$ В/см, от­вет­ст­вен­ных за удер­жа­ние элек­тро­нов в ато­мах в свя­зан­ном со­стоя­нии. Со­стоя­ние ве­ще­ст­ва под дей­ст­ви­ем столь силь­ных по­лей ра­ди­каль­но из­ме­ня­ет­ся, на пер­вый план вы­хо­дят про­бле­мы не­ли­ней­ной элек­трон­ной фи­зи­ки, ста­но­вят­ся ре­аль­но­стью пря­мые экс­пе­ри­мен­ты по на­блю­де­нию эф­фек­тов, пред­ска­зы­вае­мых кван­то­вой элек­тро­ди­на­ми­кой. Фак­ти­че­ски сфор­ми­ро­ва­лась но­вая об­ласть Н. о. – экс­тре­маль­ная Н. о., изу­чаю­щая воз­дей­ст­вие на ве­ще­ст­во све­то­вых им­пуль­сов с на­пря­жён­но­стью све­то­во­го по­ля $E⩾E_a$.

Нелинейный отклик и восприимчивости среды

От­кли­ком сре­ды на дей­ст­вие при­ло­жен­ных элек­тро­маг­нит­ных по­лей, ко­то­рый оп­ре­де­ля­ет её оп­тич. свой­ст­ва, обыч­но счи­та­ет­ся век­тор элек­трич. по­ля­ри­за­ции $\boldsymbol P$, имею­щий смысл элек­трич. ди­поль­но­го мо­мен­та еди­нич­но­го объ­ё­ма сре­ды. По­ля­ри­за­ция ве­ще­ст­ва воз­ни­ка­ет вслед­ст­вие сме­ще­ния за­ря­дов под дей­ст­ви­ем внеш­них по­лей. Ес­ли они сла­бые, то ин­ду­ци­ро­ван­ная по­ля­ри­за­ция $P_{лин}$ про­пор­цио­наль­на на­пря­жён­но­сти элек­трич. по­ля $E$. На этом пред­по­ло­жении ос­но­ва­на ли­ней­ная элек­тро­ди­на­ми­ка, и в ча­ст­но­сти ли­ней­ная оп­ти­ка. Ес­ли на ве­ще­ст­во дей­ст­ву­ет элек­тро­маг­нит­ное по­ле, со­дер­жа­щее дис­крет­ный на­бор мо­но­хро­ма­тич. волн с час­то­та­ми $ω_j$ и вол­но­вы­ми век­то­ра­ми \boldsymbol k_j, то ли­ней­ная по­ля­ри­за­ция так­же яв­ля­ет­ся сум­мой волн с те­ми же час­то­та­ми и вол­но­вы­ми век­то­ра­ми, т. е. в ли­ней­ной оп­ти­ке спра­вед­лив прин­цип су­пер­по­зи­ции. Т. о., ди­элек­трич. про­ни­цае­мость ве­ще­ст­ва в сла­бых по­лях за­ви­сит толь­ко от час­то­ты по­ля $ω$ и со­стоя­ния его по­ля­ри­за­ции и не за­ви­сит от его ам­пли­ту­ды (и ин­тен­сив­но­сти). Этот вы­вод в ли­ней­ном слу­чае от­но­сит­ся так­же к по­ве­де­нию по­ка­за­те­ля пре­лом­ле­ния и ко­эф. по­гло­ще­ния сре­ды.

Ес­ли же по­ля дос­та­точ­но силь­ные, то вы­зван­ные ими сме­ще­ния за­ря­дов ока­зы­ва­ют­ся не­ли­ней­ной функ­ци­ей по­ля, что обу­слов­ли­ва­ет не­ли­ней­ность по­ля­ри­за­ции. Не­ли­ней­ное по­ве­де­ние век­то­ра по­ля­ри­за­ции мож­но при­бли­жён­но опи­сать с по­мо­щью ря­да раз­ло­же­ния по сте­пе­ням на­пря­жён­но­сти элек­трич. по­ля $\boldsymbol E$:$$\boldsymbol P_{нл}(\boldsymbol E)=\hat{χ}^{(2)}\boldsymbol {E\!E}+\hat{χ}^{(3)}\boldsymbol{E\!E\!E}+\dots,\;\;\;\;\; (1)$$в ко­то­ром ко­эф. $\hat{χ}^{(2)}$ и $\hat{χ}^{(3)}$ – не­ли­ней­ные вос­при­им­чи­во­сти 2-го и 3-го по­ряд­ков, пред­став­ляю­щие со­бой со­от­вет­ст­вен­но тен­зо­ры 3-го и 4-го ран­гов. По­доб­ным об­ра­зом вво­дят­ся и не­ли­ней­но­сти выс­ших по­ряд­ков $\hat{χ}^{(n)}\;(n⩾4)$. При па­де­нии на сре­ду би­гар­мо­нич. све­то­во­го по­ля с час­то­та­ми $ω_1$ и $ω_2$ и вол­но­вы­ми век­то­ра­ми $k_1$ и $k_2$$$\boldsymbol E=\boldsymbol E(ω_1)+\boldsymbol E(ω_2)= \boldsymbol e_1A_1\text{exp}i(ω_1t-\boldsymbol k_1\boldsymbol r) + \boldsymbol e_2A_2\text{exp}\:i(ω_2t-\boldsymbol k_2\boldsymbol r)\;\;\;\;\;(2)$$($e_j$ – еди­нич­ный век­тор по­ля­ри­за­ции вол­ны, $j=1, 2$) за счёт квад­ра­тич­ной не­ли­ней­но­сти по­ро­ж­да­ют­ся вол­ны по­ля­ри­за­ции на час­то­тах $2ω_j, ω_1±ω_2$ с со­от­вет­ст­вую­щи­ми вол­но­вы­ми век­то­ра­ми $2\boldsymbol k_j$ и $\boldsymbol k_1±\boldsymbol k_2: \boldsymbol P^{(2)}(ω)=\hat{χ}^{(2)}(ω=ω_1±ω_2)×\boldsymbol E(ω_1)\boldsymbol E(±ω_2)$, где тен­зор $\hat{χ}^{(2)}(ω=ω_1±ω_2)$ за­ви­сит от час­тот ис­ход­ных волн и от ре­зуль­ти­рую­щей час­то­ты. Но­вые вол­ны по­ля­ри­за­ции пред­став­ля­ют со­бой рас­пре­де­лён­ный ис­точ­ник, из­лу­чаю­щий элек­тро­маг­нит­ные вол­ны на ком­би­ни­ро­ван­ных час­то­тах. Т. о., прин­цип су­пер­по­зи­ции на­ру­ша­ет­ся за счёт не­линей­но­сти. Ес­ли $ω_1=ω_2$, то воз­ни­ка­ет не­ли­ней­ная по­ля­ри­за­ция на ну­ле­вой час­то­те. Напр., ес­ли ин­тен­сив­ный све­то­вой пу­чок про­хо­дит че­рез пье­зок­ри­сталл, то по­яв­ля­ет­ся по­сто­ян­ное на­пря­же­ние – про­исходит оп­тич. вы­прям­ле­ние. Ес­ли $ω_2=0$, то $ω=ω_1$ и не­ли­ней­ная по­ля­ри­за­ция $\boldsymbol P^{(2)}(ω_1)$ опи­сы­ва­ет ли­ней­ный элек­тро­оп­тич. эф­фект Пок­кель­са.

Ана­ло­гич­но, ку­би­че­ское по по­лю сла­гае­мое от­вет­ст­вен­но за фор­ми­ро­ва­ние волн по­ля­ри­за­ции на час­то­тах, яв­ляю­щих­ся ком­би­на­ци­ей трёх час­тот ис­ход­ных элек­тро­маг­нит­ных волн $ω=ω_1±ω_2±ω_3$ с вол­но­вы­ми век­то­ра­ми $\boldsymbol k=\boldsymbol k_1±\boldsymbol k_2±\boldsymbol k_3$:$$\boldsymbol P^{(3)}(ω)=\hat{χ}^{(3)}(ω=ω_1±ω_2±ω_3)×\boldsymbol E(ω_1)\boldsymbol E(±ω_2)\boldsymbol E(±ω_3).\;\;\;\;\;(3)$$

Здесь $\hat{χ}^{(3)}(ω=ω_1±ω_2±ω_3)$ – не­ли­ней­ная вос­при­им­чи­вость 3-го по­ряд­ка с со­от­вет­ст­вую­щей час­тот­ной за­ви­си­мо­стью.

Наи­бо­лее ин­фор­ма­тив­ным яв­ля­ет­ся т. н. мик­ро­струк­тур­ный под­ход к рас­чё­ту оп­тич. от­кли­ка. В этом слу­чае по­ля­ри­за­ция ве­ще­ст­ва рас­смат­ри­ва­ет­ся как сум­ма ин­ду­ци­ро­ван­ных по­лем ди­поль­ных мо­мен­тов эле­мен­тар­ных из­лу­ча­те­лей (ато­мов, мо­ле­кул и т. д.): $$\boldsymbol P=\sum _{a} N_a\boldsymbol p_a,$$где $N_a$ – плот­ность чис­ла ато­мов или мо­ле­кул дан­но­го сор­та $a,\; \boldsymbol p_a=〈\boldsymbol d_a〉$ – ср. зна­че­ние ди­поль­но­го мо­мен­та. Кван­то­во­ме­ха­нич. рас­чёт в рам­ках тео­рии воз­му­ще­ний да­ёт:$$\boldsymbol p=\hat{α}^{(1)}\boldsymbol E+\hat{α}^{(2)}\boldsymbol {E\!E}+\hat{α}^{(3)}\boldsymbol {E\!E\!E}+\dots,\;\;\;\;\; (4)$$где $\hat{α}^{(n)}$ – тен­зо­ры атом­ной (или мо­ле­куляр­ной) по­ля­ри­зуе­мо­сти $n$-го по­ряд­ка, ха­рак­те­ри­зую­щие от­клик свя­зан­ных элек­тро­нов. То­гда вос­при­им­чи­во­сти ве­ще­ст­ва вы­ра­жа­ют­ся че­рез сред­ние по ори­ен­та­циям по­ля­ри­зуе­мо­сти: $\hat{χ}^{(n)}=N〈\hat{α}^{(n)}〉$ . По­это­му, кро­ме элек­трон­но­го вкла­да, не­ли­ней­ность мак­ро­ско­пич. от­кли­ка мо­жет быть свя­за­на с влия­ни­ем по­ля на ори­ен­та­цию ани­зо­троп­ных мо­ле­кул (т. н. ори­ен­та­ци­он­ный ме­ха­низм не­ли­ней­но­сти), а так­же на плот­ность чис­ла ато­мов и мо­ле­кул $N$. В по­след­нем слу­чае гл. роль иг­ра­ют элек­тро­стрик­ци­он­ный ме­ха­низм, свя­зан­ный со втя­ги­ва­ни­ем мо­ле­кул в об­ласть бо­лее силь­но­го по­ля, и тем­пе­ра­тур­ный ме­ха­низм, в ос­но­ве ко­то­ро­го ле­жит на­грев сре­ды оп­тич. из­лу­че­ни­ем.

Кван­то­во­ме­ха­нич. под­ход по­ка­зы­ва­ет, что в ос­но­ве не­ли­ней­но­го от­кли­ка, от­вет­ст­вен­но­го за мно­го­вол­но­вые взаи­мо­дей­ст­вия, ле­жат мно­го­фо­тон­ные про­цес­сы. Так, квад­ра­тич­ную не­ли­ней­ность фор­ми­ру­ют трёх­фо­тон­ные про­цес­сы, при ко­то­рых в од­ном ак­те ве­ще­ст­во по­гло­ща­ет два фо­то­на с энер­гия­ми $ℏω_1$ и $ℏω_2$ ($ℏ$ – по­сто­ян­ная План­ка) и ис­пус­ка­ет фо­тон с сум­мар­ной энер­ги­ей $ℏω_3=ℏω_1+ℏω_2$, ли­бо, на­обо­рот, по­гло­ща­ет фо­тон $ℏω_3$ и ис­пус­ка­ет два фо­то­на, сум­мар­ная энер­гия ко­то­рых $ℏω_1+ℏω_2=ℏω_3$.

Про­цес­сы, при ко­то­рых ко­неч­ное кван­то­вое со­стоя­ние мно­го­фо­тон­но­го пе­ре­хо­да сов­па­да­ет с ис­ход­ным, на­зы­ва­ют ко­ге­рент­ны­ми, т. к. фа­зы взаи­мо­дей­ст­вую­щих волн ока­зы­ва­ют­ся жё­ст­ко свя­зан­ны­ми ме­ж­ду со­бой. Та­кие про­цес­сы при­ня­то ещё на­зы­вать па­ра­мет­ри­че­ски­ми: взаи­мо­дей­ст­вие волн в этом слу­чае обу­слов­ле­но мо­ду­ля­ци­ей па­ра­мет­ров сре­ды, од­на­ко энер­го­об­мен ме­ж­ду вол­на­ми про­ис­хо­дит в ко­неч­ном счё­те без пе­ре­да­чи энер­гии (а сле­до­ва­тель­но, и им­пуль­са) сре­де. К па­ра­мет­ри­че­ским от­но­сят­ся поч­ти все про­цес­сы взаи­мо­дей­ст­вия в сре­дах с квад­ра­тич­ной не­ли­ней­но­стью: ге­не­ра­ция гар­мо­ник, про­цес­сы сло­же­ния и вы­чи­та­ния час­тот оп­тич. из­лу­че­ния, па­ра­мет­рич. уси­ле­ние и ге­не­ра­ция и др. Про­цес­сы, в ко­то­рых сре­да ме­ня­ет своё энер­ге­тич. со­стоя­ние в ре­зуль­та­те не­ли­ней­но­го взаи­мо­дей­ст­вия, от­но­сят к не­па­ра­мет­ри­че­ским, это мно­го­фо­тон­ное по­гло­ще­ние, на­сы­ще­ния эф­фект, про­стей­шие ва­ри­ан­ты вы­ну­ж­ден­но­го рас­сея­ния.

Спек­траль­ные ком­по­нен­ты тен­зо­ра вос­при­им­чи­во­сти $\hat{χ}^{(2)}(ω=ω_1±ω_2)$ свя­за­ны с бы­ст­ры­ми (элек­трон­ны­ми) ме­ха­низ­ма­ми не­ли­ней­но­го от­кли­ка, для ко­то­рых $\tau_{нл}⩽\omega^{-1}_j≈1\!0^{–14}$ с. Эти про­цес­сы при­во­дят к мо­ду­ля­ции ди­элек­трич. про­ни­цае­мо­сти сре­ды с оп­тич. час­то­той. Наи­бо­лее важ­ный сре­ди них – не­ре­зо­нанс­ный от­клик свя­зан­ных оп­тич. элек­тро­нов: ($E_a≈5·1\!0^9$ В/см – внут­ри­атом­ная на­пря­жён­ность по­ля в ато­ме во­до­ро­да), т. е. $\hat{χ}^{(2)}∼ 1\!0^{–7}$ (в сис­те­ме СГС). Ре­аль­ные зна­че­ния $\hat{χ}^{(2)}$ в ви­ди­мом диа­па­зо­не для ди­элек­три­ков ле­жат в пре­де­лах от $1\!0^{–9}$ (кварц) до $1\!,\!7·1\!0^{–7}$ (кри­сталл ба­рий – на­трия нио­бат с наи­боль­шей не­ли­ней­но­стью). Зна­чи­тель­но бóльшие зна­че­ния $\hat{χ}^{(2)}$ в по­лу­про­вод­ни­ках; в $\ce{GaAs}$ на дли­не вол­ны $λ=1\!,\!06$ мкм $\hat{χ}^{(2)}(2ω)≈5\!,\!2·1\!0^{–7}$, в кри­стал­ле Те в ИК-диа­па­зо­не ($λ=10,\!6$ мкм) $\hat{χ}^{(2)}(2ω)≈2\!,\!2·1\!0^{–6}$. Т. о., раз­ли­чие в ве­ли­чи­нах не­ли­ней­ных вос­при­им­чи­во­стей дос­ти­га­ет поч­ти трёх по­ряд­ков. Ко­ли­че­ст­вен­ный рас­чёт $\hat{χ}^{(2)}$ для кон­крет­ных кри­стал­лов ос­но­вы­ва­ет­ся в боль­шин­ст­ве слу­ча­ев на по­лу­фе­но­ме­но­ло­гич. мо­де­лях.

В элек­тро­ди­поль­ном при­бли­же­нии квад­ра­тич­ная вос­при­им­чи­вость $\hat{χ}^{(2)}$, как и все вос­при­им­чи­во­сти чёт­ных по­ряд­ков, рав­на ну­лю в изо­троп­ных и цен­тро­сим­мет­рич­ных сре­дах.

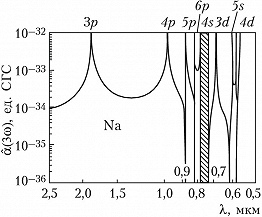
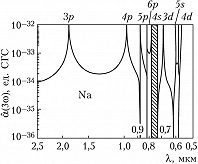
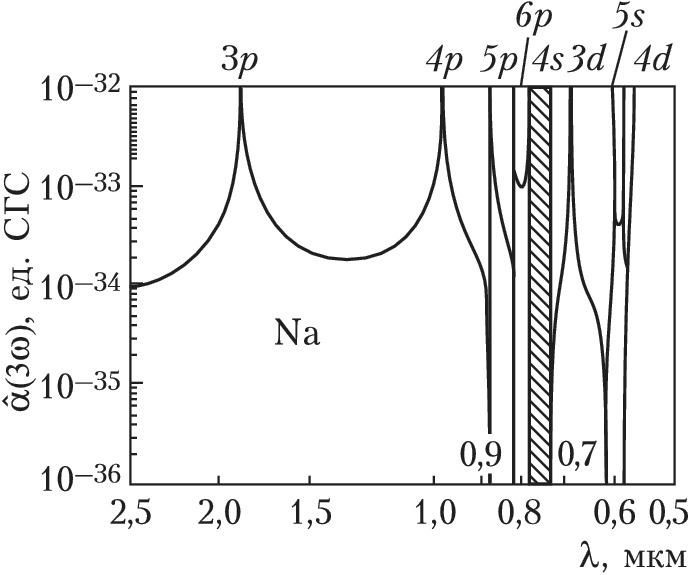
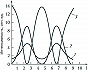
Ку­бич­еская не­ли­ней­ная вос­при­им­чи­вость $\hat{χ}^{(3)}$ от­лич­на от ну­ля прак­ти­че­ски в лю­бых сре­дах, вклю­чая и цен­тро­сим­мет­рич­ные: га­зы, жид­ко­сти, аморф­ные и кри­стал­лич. твёр­дые те­ла. В этих сре­дах в ре­зуль­та­те че­ты­рёх­час­тот­ных взаи­мо­дей­ст­вий би­гар­мо­нич. по­ле (2) воз­бу­ж­да­ет ши­ро­кий спектр не­ли­ней­ной по­ля­ри­за­ции на выс­ших гар­мо­ни­ках и ком­би­на­ци­он­ных час­то­тах: $3ω_1, 3ω_2, 2ω_1±ω_2, 2ω_2±ω_1$ и т. п. При этом свой­ст­ва не­ли­ней­ной вос­при­им­чи­во­сти $\hat{χ}^{(3)}$⁾ и ха­рак­тер про­цес­сов взаи­мо­дей­ст­вия су­щест­вен­но за­ви­сят от на­ли­чия или от­сут­ст­вия ре­зо­нан­сов. Ес­ли час­то­ты по­лей и их ком­би­на­ции ти­па $ω_i±ω_j$ да­ле­ки от собств. час­тот кван­то­вых пе­ре­хо­дов, то по­ля­ри­зуе­мость $\hat{α}^{(3)}$ – дей­ст­ви­тель­ная ве­ли­чи­на и опи­сы­ва­ет че­ты­рёх­фо­тон­ные па­ра­мет­рич. про­цес­сы. Ес­ли к.-л. из час­тот $ω_j$ ока­зы­ва­ет­ся вбли­зи од­но­фо­тон­но­го ре­зо­нан­са или ком­би­на­ция час­тот $ω_i±ω_j$ близ­ка к двух­фо­тон­но­му ре­зо­нан­су, то по­ля­ри­зуе­мость рез­ко воз­рас­та­ет и ста­но­вит­ся ком­плекс­ной ве­ли­чи­ной. В этих слу­ча­ях про­цес­сы взаи­мо­дей­ст­вия приобретают бо­лее слож­ный характер. Напр., па­ра­мет­рич. про­цесс ге­не­ра­ции 3-й гар­мо­ни­ки при двух­фо­тон­ном ре­зо­нан­се со­про­во­ж­да­ет­ся про­цес­са­ми двух­фо­тон­но­го по­гло­ще­ния и вы­ну­ж­ден­но­го ком­би­на­ци­он­но­го рас­сея­ния. На рис. 2 при­ве­де­ны тео­ре­тич. зна­че­ния ку­би­че­ской по­ля­ри­зуе­мо­сти $\hat{α}^{(3)}(3ω)$ и внут­рен­няя структура возбуждённых энер­ге­тич. уров­ней ато­мов $\ce{Na}$. Рез­кие воз­рас­та­ния ку­би­че­ской по­ля­ри­зуе­мо­сти про­ис­хо­дят вбли­зи ре­зо­нан­сов.

Рис. 2. Теоретические значения кубической поляризуемости ˆαα(3)(3ω) атома Na в зависимости от длины волны. Заштрихована область перекрывающихся резонансов.

Ку­би­че­ские вос­при­им­чи­во­сти $\hat{χ}^{(3)}$ для силь­но раз­ли­чаю­щих­ся час­тот при от­сут­ст­вии ре­зо­нан­са обу­слов­ле­ны ма­ло­инер­ци­он­ны­ми (напр., элек­трон­ны­ми) ме­ха­низ­ма­ми не­ли­ней­но­го от­кли­ка. Для оцен­ки спек­траль­ной ком­по­нен­ты $\hat{χ}^{(3)}(3ω)$, свя­зан­ной с не­ре­зо­нанс­ным элек­трон­ным от­кли­ком кон­ден­си­ро­ван­ной сре­ды, мож­но по­ла­гать $\hat{χ}^{(3)}(3ω) ∝ E_a^{-2}$. Оцен­ка $\hat{χ}^{(3)}(3ω)∼1\!0^{–13}–1\!0^{–14}$ близ­ка к зна­че­ни­ям, из­ме­ряе­мым в оп­ти­че­ски про­зрач­ных жид­ко­стях и ди­элек­три­ках. В по­ве­де­нии $\hat{χ}^{(3)}$ в га­зах го­раз­до силь­нее, чем в по­ве­де­нии $\hat{χ}^{(2)}$, про­яв­ля­ют­ся ин­ди­ви­ду­аль­ные свой­ст­ва ато­мов и мо­ле­кул. Осо­бен­но яр­ко раз­ли­чия вы­ра­же­ны в ре­зо­нанс­ных свой­ст­вах $\hat{χ}^{(3)}$ (для раз­ре­жен­но­го га­за $\hat{χ}^{(3)}N\hat{α}^{(3)}$).

Че­ты­рёх­час­тот­ные не­ли­ней­ные взаи­мо­дей­ст­вия на ку­бической не­ли­ней­но­сти при­во­дят не толь­ко к ге­не­ра­ции волн на но­вых час­то­тах, но и к воз­ник­но­ве­нию не­ли­ней­ной по­ля­ри­за­ции на час­то­тах ис­ход­ных волн. К это­му при­во­дят взаи­мо­дей­ст­вия на час­то­тах $$ω_1=ω_1+ω_1-ω_1,\; ω_1=ω_1+ω_2-ω_2,\;\;\;\;\;(5)$$за ко­то­рые от­вет­ст­вен­ны час­тот­ные ком­по­нен­ты по­ля­ри­за­ции$$P_{нл}(ω_j)=\hat{χ}^{(3)}(ω_j)E(ω_j)E(ω_j)E^*\!(ω_j),\;\;\;\;\;  (6а)$$$$P_{нл}(ω_j)=\hat{χ}^{(3)}(ω_j)E(ω_j)E(ω_i)E^*\!(ω_i).\;\;\;\;\;  (6б)$$

В слу­чае от­сут­ст­вия ре­зо­нан­са вос­при­им­чи­во­сти $\hat{χ}^{(3)}$  – дей­ст­ви­тель­ные ве­ли­чи­ны и фор­му­лы (6 а, б) оп­ре­де­ля­ют не­ли­ней­ные до­бав­ки $n_2$ к по­ка­за­те­лю пре­лом­ле­ния для вол­ны на час­то­те $ω_j$, про­пор­цио­наль­ные ин­тен­сив­но­сти са­мой вол­ны [са­мо­воз­дей­ст­вие, фор­му­ла (6а)] или др. вол­ны [кросс-взаи­мо­дей­ст­вие, фор­му­ла (6б)]. Пол­ный по­ка­за­тель пре­лом­ле­ния ку­бической сре­ды$$n=n_0+n_2I,\;\;\;\;\;(7)$$где $I$ – ин­тен­сив­ность вол­ны, ко­эф. $n_2∼\hat{χ}^{(3)}$. Обу­слов­лен­ная бы­ст­рым не­ре­зо­нанс­ным от­кли­ком оп­тич. элек­тро­нов до­бав­ка $n_2I$ от­но­си­тель­но не­ве­ли­ка. При­бли­зи­тель­ные зна­че­ния $n_2$ для мн. кри­стал­лов и жид­ко­стей $n_2≈1\!0^{–13}$ см²/кВт. По­это­му да­же для ин­тен­сив­но­стей, близ­ких к про­бой­ным $I_{проб}$, до­бав­ка $Δn=n_2I_{проб}$ весь­ма ма­ла, $Δn≪n_0$.

Рис. 3. Значения нелинейного коэффициента n2 для оптических материалов на плоскости (n2, τнл). Штриховыми кривыми выделены области с различными механизмами нелинейности.

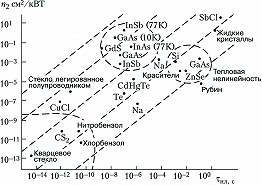
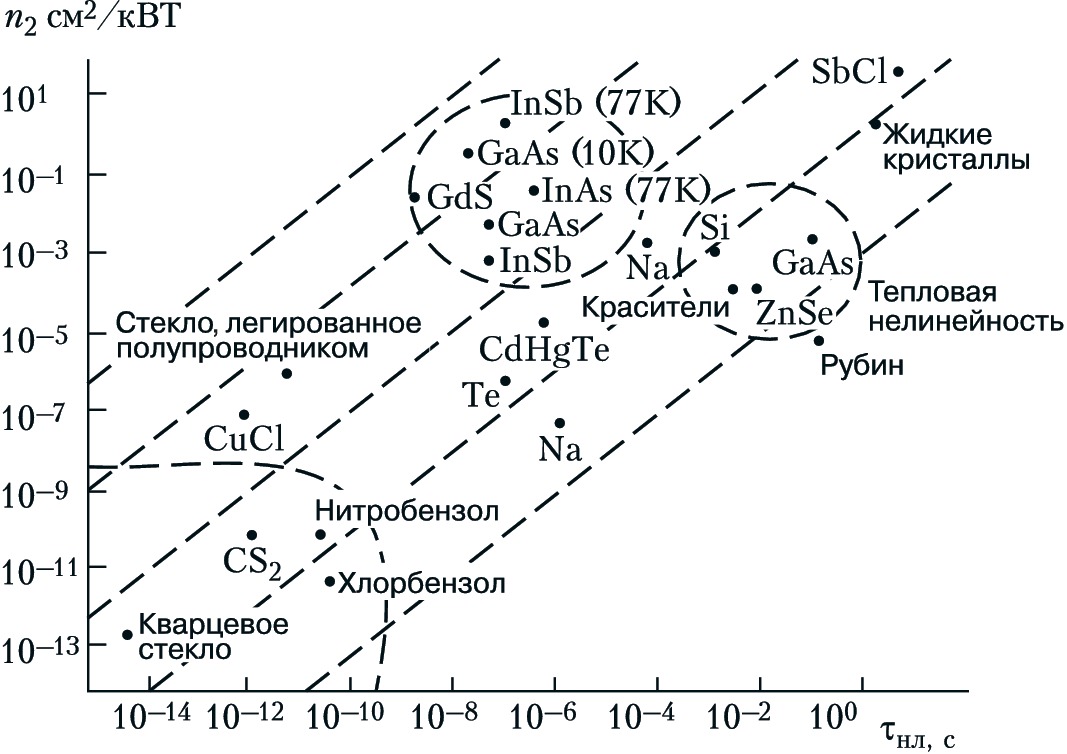
Су­ще­ст­ву­ет мно­го дру­гих (хо­тя и бо­лее инер­ци­он­ных) ме­ха­низ­мов, при­во­дя­щих к зна­чи­тель­но бо­лее силь­ной не­ли­ней­но­сти по­ка­за­те­ля пре­лом­ле­ния. К ним от­но­сят­ся ре­зо­нанс­ные не­ли­ней­но­сти в по­лу­про­вод­ни­ках (эк­си­тон­ные ре­зо­нан­сы), фо­то­реф­рак­тив­ный эф­фект в не­ор­га­нич. кри­стал­лах, ори­ен­та­ция ани­зо­троп­ных мо­ле­кул в све­то­вом по­ле, оп­тич. на­грев сре­ды и т. п. Диа­па­зон зна­че­ний не­ли­ней­но­го па­ра­мет­ра $n_2$ пре­вы­ша­ет 10 по­ряд­ков (рис. 3). Не­смот­ря на су­ще­ст­вен­ное раз­ли­чие фи­зич. ме­ха­низ­мов не­ли­ней­но­сти, мно­го­числ. дан­ные не­пло­хо укладываются на за­ви­си­мость $n_2∝t_{нл}$ (штриховые прямые; $τ_{нл}$ – вре­мя не­ли­ней­но­го от­кли­ка), т. е. уве­ли­че­ние инер­ци­он­но­сти от­кли­ка при­во­дит к рос­ту $n_2$. К ори­ента­ци­он­но­му ме­ха­низ­му не­ли­ней­но­сти в жид­ких кри­с­тал­лах, при­во­дя­ще­му к $n_2> 0\!,\!1$ см²/кВт, с пол­ным ос­но­ва­ни­ем при­ме­ни­мо оп­ре­де­ле­ние «ги­гант­ские оп­тич. не­ли­ней­но­сти».

В ре­зо­нанс­ном слу­чае $\hat{χ}^{(3)}$ яв­ля­ет­ся ком­плекс­ной ве­ли­чи­ной, мни­мая часть ко­то­рой от­вет­ст­вен­на за не­ли­ней­ное по­гло­ще­ние или уси­ле­ние со­от­вет­ст­вую­щей вол­ны. Так, в слу­чае вы­ро­ж­ден­но­го по час­то­те двух­фо­тон­но­го ре­зо­нан­са мни­мая часть $\hat{χ}^{(3)}(ω_1)$ в фор­му­ле (6а) опи­сы­ва­ет ос­лаб­ле­ние вол­ны на час­то­те $ω_1$ вслед­ст­вие по­гло­ще­ния. При на­ли­чии ком­би­на­ци­он­но­го ре­зо­нан­са по­ля­ри­за­ция [фор­му­ла (6б)] от­вет­ст­вен­на за уси­ле­ние сто­ксо­вой ком­по­нен­ты и ос­лаб­ле­ние вол­ны на­кач­ки при вы­ну­ж­ден­ном ком­би­на­ци­он­ном рас­сея­нии. Опи­са­ние оп­тич. от­кли­ка ве­ще­ст­ва с по­мо­щью вос­при­им­чи­во­стей спра­вед­ли­во толь­ко для не очень силь­ных ква­зи­мо­но­хро­ма­тич. по­лей.

Волновая и квантовая нелинейная оптика

Воз­ни­каю­щая в сре­де не­ли­ней­ная по­ля­ри­за­ция воз­бу­ж­да­ет элек­тро­маг­нит­ную вол­ну, имею­щую те же час­то­ту и вол­но­вой век­тор, что и вол­на не­ли­ней­ной по­ля­ри­за­ции. Ин­тер­фе­рен­ция вы­нуж­ден­ных волн со сво­бод­ны­ми вол­на­ми сре­ды оп­ре­де­ля­ет ди­на­ми­ку раз­ви­тия не­ли­ней­но­го вол­но­во­го про­цес­са во вре­ме­ни и в про­стран­ст­ве. По­сколь­ку ха­рак­тер ин­тер­фе­рен­ции сво­бод­ных и вы­ну­ж­ден­ных волн силь­но за­ви­сит от дис­пер­сии сре­ды, её дис­пер­си­он­ные свой­ст­ва ре­шаю­щим об­ра­зом влия­ют на фор­ми­ро­ва­ние не­ли­ней­ных волн. В элек­тро­ди­на­ми­ке силь­но­дис­пер­ги­рую­щих сла­бо­не­ли­ней­ных сред вы­де­ля­ют не­ли­ней­ные взаи­мо­дей­ст­вия волн с разл. час­то­та­ми и вол­но­вы­ми век­то­ра­ми и са­мо­воз­дей­ст­вие волн, обу­слов­лен­ные за­ви­си­мо­стью по­ка­за­те­ля пре­лом­ле­ния от ин­тен­сив­но­сти вол­ны.

Рис. 4. Зависимость амплитуд основной волны ρ1 и 2-й гармоники ρ2 при фазовом синхронизме от расстояния, которое проходит волна; $l= \beta\rha Br_10^-1$– характерная длина взаимодействи...

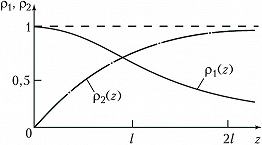
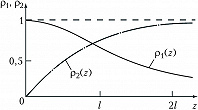
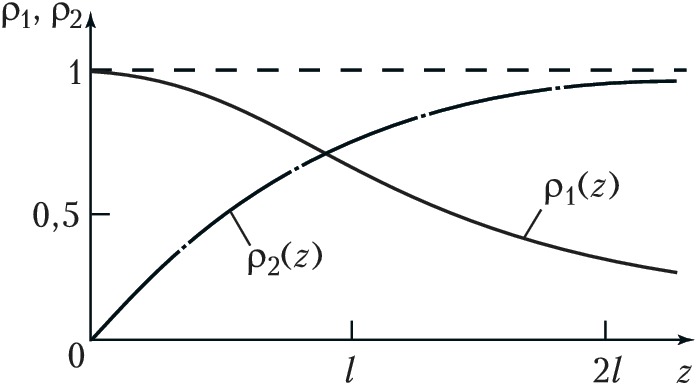
При не­ли­ней­ном па­ра­мет­рич. взаи­мо­дей­ст­вии волн очень су­ще­ст­вен­но со­гла­со­ва­ние фа­зо­вых ско­ро­стей не­ли­ней­ной по­ля­ри­за­ции и сво­бод­ных волн, т. е. вы­пол­не­ние ус­ло­вия фа­зо­во­го син­хро­низ­ма. Имен­но при этом ус­ло­вии про­ис­ходит син­фаз­ное сло­же­ние по­лей од­ной и той же час­то­ты в разл. уча­ст­ках не­ли­ней­ной сре­ды. Так, при ге­не­ра­ции 2-й оп­тич. гар­мо­ни­ки (уд­вое­нии час­то­ты, $ω_2=2ω_1$) в слу­чае од­но­на­прав­лен­но­го рас­про­стра­не­ния волн ус­ло­вие фа­зо­во­го син­хро­низ­ма (кол­ли­не­ар­ный фа­зо­вый син­хро­низм) име­ет вид: $k_2=2k_1$, где $k_1$ – вол­но­вое чис­ло ис­ход­ной вол­ны, $k_2$ – вол­но­вое чис­ло 2-й гар­мо­ни­ки. Для пло­ских мо­но­хро­ма­тич. волн из­ме­не­ние ам­пли­туд взаи­мо­дей­ст­вую­щих волн при уд­вое­нии оп­тич. час­то­ты опи­сы­ва­ет­ся вы­ра­же­ния­ми (ко­ор­ди­на­та $z⩾0$):$$\begin{matrix}ρ_1(z)=ρ_{10}\text{sech}(βρ_{10}z),\\ ρ_2(z)=ρ_{10}\text{th}(βρ_{10}z),\end{matrix}\;\;\;\;\; (8)$$где $ρ_1, ρ_2$ – ам­пли­ту­ды осн. вол­ны и 2-й гар­мо­ни­ки со­от­вет­ст­вен­но, $ρ_{10}$ – на­чаль­ное зна­че­ние ам­пли­ту­ды, $β$ – не­ли­ней­ный ко­эф. свя­зи волн, $β∝\hat{χ}^{(2)}$. Из гра­фи­ков функ­ций (8), изо­бра­жён­ных на рис. 4, сле­ду­ет, что вся энер­гия осн. вол­ны пе­ре­хо­дит в энер­гию 2-й гар­мо­ни­ки при на­ли­чии фа­зо­во­го син­хро­низ­ма. Это­го нель­зя дос­тичь при фа­зо­вой рас­строй­ке $Δk=k_2-2k_1≠0$. Наи­бо­лее эф­фек­тив­ное пре­об­ра­зо­ва­ние час­то­ты сверх­ко­рот­ких ла­зер­ных им­пуль­сов про­ис­хо­дит в ус­ло­ви­ях фа­зо­во­го синхро­низ­ма и груп­по­во­го син­хро­низ­ма (ра­вен­ст­ва груп­по­вых ско­ро­стей взаи­мо­дей­ст­вую­щих волн).

Ус­ло­вие кол­ли­не­ар­но­го фа­зо­во­го син­хро­низ­ма в изо­троп­ных сре­дах вы­пол­ня­ет­ся (из-за час­тот­ной дис­пер­сии) толь­ко в об­лас­ти ано­маль­ной дис­пер­сии, а в ани­зо­троп­ных средах – и в об­лас­ти нор­маль­ной дис­пер­сии при взаи­мо­дей­ст­вии волн разл. по­ля­ри­за­ций. Хо­тя все­гда $n_o(ω_1)< n_o(ω_2)$ и $n_e(\omega_1)< n_e(\omega _2)$ (ин­дек­сы $o$ и $e$ от­но­сят­ся со­от­вет­ст­вен­но к обык­но­вен­ным и не­обык­но­вен­ным вол­нам), од­на­ко при не слиш­ком ма­лых па­ра­мет­рах ани­зо­тро­пии воз­мож­но $n_o(ω_1)⩾n_e(ω_2)$ (от­ри­ца­тель­ные кри­стал­лы) или $n_е(ω_1)⩾n_o(ω_2)$ (по­ло­жи­тель­ные кри­стал­лы). При не­ко­то­ром уг­ле $θ$ ме­ж­ду на­прав­ле­ни­ем рас­про­стра­не­ния и оп­тич. осью в от­ри­ца­тель­ном не­ли­ней­ном кри­стал­ле мож­но реа­ли­зо­вать ус­ло­вие фа­зо­во­го син­хро­низ­ма, ко­то­рое в слу­чае ге­не­ра­ции 2-й гар­мо­ни­ки име­ет вид $n_e(ω_2=2ω_1)=n_o(ω_1)$.

Рис. 5. Динамика изменения интенсивности волн при трёхчастотном параметрическом взаимодействии. По оси ординат отложены относительные интенсивности волн сигнала I1/I10 (кривая 1), разностной частоты I...

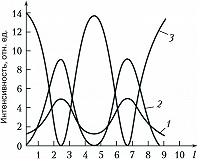
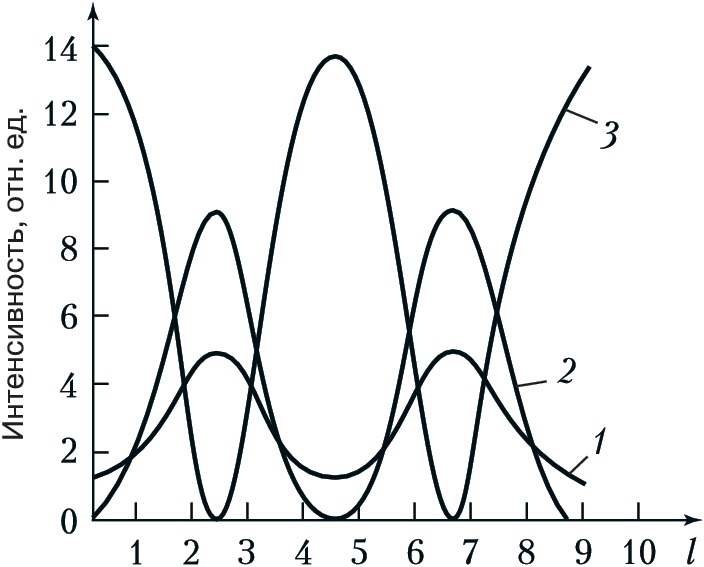
В не­ли­ней­ной сре­де с квад­ра­тич­ной не­ли­ней­но­стью под дей­ст­ви­ем би­гар­мо­нич. по­ля (2) мо­гут реа­ли­зо­вать­ся не­вы­ро­ж­ден­ные трёх­час­тот­ные про­цес­сы, в ко­то­рых воз­бу­ж­да­ют­ся но­вые час­то­ты и про­ис­хо­дит уси­ле­ние волн. Наи­бо­лее ин­тен­сив­ную из двух па­даю­щих на сре­ду волн с час­то­той $ω_н$ на­зы­ва­ют вол­ной на­кач­ки. В по­ле та­кой вол­ны мож­но осу­ще­ст­вить как па­ра­мет­рич. про­цесс уси­ле­ния при вы­со­ко­час­тот­ной на­кач­ке $ω_н=ω_1+ω_2$ ($ω_1, ω_2$ – час­то­ты уси­ли­вае­мых волн), так и па­ра­мет­рич. пре­об­ра­зо­ва­ние час­то­ты $ω_2=ω_н±ω_1$ ($ω_2$ – час­то­та ге­не­ри­руе­мой вол­ны, $ω_1$ – час­то­та сла­бой вол­ны, по­сту­паю­щей на вход не­ли­ней­ной сре­ды). При этом знак «+» со­от­вет­ст­ву­ет ге­не­ра­ции сум­мар­ной час­то­ты, знак «–» – ге­не­ра­ции раз­но­ст­ной час­то­ты. При па­ра­мет­рич. взаи­мо­дей­ст­вии уси­ли­вае­мую вол­ну час­то на­зы­ва­ют сиг­наль­ной вол­ной, а на­ро­ж­даю­щую­ся при этом вол­ну – хо­ло­стой вол­ной. Как и в слу­чае вы­ро­ж­ден­но­го трёх­час­тот­но­го взаи­мо­дей­ст­вия (уд­вое­ния час­то­ты), наи­бо­лее эф­фек­тив­ный энер­го­об­мен ме­ж­ду взаи­мо­дей­ст­вую­щи­ми вол­на­ми реа­ли­зу­ет­ся при вы­пол­не­нии ус­ло­вий фа­зо­во­го и груп­по­во­го син­хро­низ­ма. Рисунок 5 ил­лю­ст­ри­ру­ет ди­на­ми­ку энер­го­об­ме­на при па­ра­мет­рич. взаи­мо­дей­ст­вии. Про­стран­ст­вен­ные бие­ния трёх волн, изо­бра­жён­ные на рис. 5, пред­став­ля­ют со­бой пе­рио­дич. по­сле­до­ва­тель­ность про­цес­сов па­ра­мет­рич. уси­ле­ния в по­ле ин­тен­сив­ной вы­со­ко­час­тот­ной вол­ны на­кач­ки $ω_н→ω_1+ω_2$ и сло­же­ния час­тот $ω_1+ω_2→ω_н$.

Взаи­мо­дей­ст­вия све­то­вых волн в сре­дах с ку­би­ческой не­ли­ней­но­стью очень раз­но­об­раз­ны. В об­щем слу­чае ме­ж­ду час­то­та­ми $ω_j$ и вол­но­вы­ми век­то­ра­ми $k_j$ волн в та­кой сре­де име­ют ме­сто со­от­но­ше­ния:$$\begin{matrix}ω_4→±ω_1±ω_2±ω_3,\\k_4=±k_1±k_2±k_3.\end{matrix}\;\;\;\;\;(9)$$Рас­смот­рен­ные вы­ше час­тот­ные со­от­но­ше­ния для та­ких сред яв­ля­ют­ся ча­ст­ным слу­ча­ем фор­му­лы (9).

Трёх- и че­ты­рёх­час­тот­ные па­ра­мет­рич. взаи­мо­дей­ст­вия иг­ра­ют фун­дам. роль в Н. о. Трёх­час­тот­ное па­ра­мет­рич. уси­ле­ние при вы­со­ко­час­тот­ной на­кач­ке ле­жит в ос­но­ве дей­ст­вия пе­ре­страи­вае­мых ПГС: при фик­си­ро­ван­ной час­то­те на­кач­ки $ω_н$ час­то­ты уси­ли­вае­мых волн $ω_1$ и $ω_2$ мож­но пе­ре­страи­вать, из­ме­няя дис­пер­си­он­ные свой­ст­ва сре­ды. Та­кие ге­не­ра­то­ры све­та мо­гут плав­но пе­ре­страи­вать­ся во всём ви­ди­мом диапазоне и ближ­нем ИК-диа­па­зо­не. Ис­поль­зо­ва­ние сред с про­стран­ст­вен­ной дис­пер­си­ей (с за­ви­си­мо­стью ди­элек­трич. про­ни­цае­мо­сти от вол­но­во­го век­то­ра) по­зво­ля­ет по­лу­чать при пре­обра­зо­ва­нии час­тот све­то­вые пуч­ки со слож­ной по­ля­ри­за­ци­он­ной струк­ту­рой.

Па­ра­мет­рич. взаи­мо­дей­ст­вия яв­ля­ют­ся ис­точ­ни­ка­ми не­клас­сич. по­лей: по­ля в фо­ков­ском со­стоя­нии, квад­ра­тур­но-сжа­то­го и по­ля­ри­за­ци­он­но-сжа­то­го све­та, све­та в пе­ре­пу­тан­ном кван­то­вом со­стоя­нии. В та­ких по­лях уро­вень флук­туа­ций не­ко­то­рых кван­то­вых па­ра­мет­ров мень­ше, чем для по­лей в ко­ге­рент­ном со­стоя­нии, а пе­ре­пу­тан­ные со­стоя­ния яв­ля­ют­ся су­гу­бо кван­то­вы­ми (см. Кван­то­вая оп­ти­ка). Кван­то­вые осо­бен­но­сти па­ра­мет­рич. про­цес­сов ис­поль­зу­ют­ся при кван­то­вой об­ра­бот­ке изо­бра­же­ний. Про­цесс ге­не­ра­ции сум­мар­ной час­то­ты ле­жит в ос­но­ве пре­об­ра­зо­ва­ния изо­бра­же­ния из ИК-диа­па­зо­на в ви­ди­мый диа­па­зон, в ко­то­ром фо­то­при­ём­ни­ки об­ла­да­ют боль­шей чув­ст­ви­тель­но­стью. Ге­нера­ция раз­но­ст­ных час­тот на ос­но­ве не­вы­ро­ж­ден­но­го трёх­час­тот­но­го взаи­мо­дей­ст­вия со­став­ля­ет ос­но­ву од­но­го из ме­то­дов по­лу­че­ния элек­тро­маг­нит­ных волн в те­ра­гер­це­вом диа­па­зо­не час­тот.

Важ­ным клас­сом не­ли­ней­ных оп­тич. эф­фек­тов яв­ля­ют­ся про­цес­сы вы­ну­ж­ден­но­го рас­сея­ния све­та (ВРС), при ко­то­рых мощ­ная вол­на на­кач­ки вме­сте с рас­се­ян­ной вол­ной соз­да­ёт ко­ге­рент­ные эле­мен­тар­ные воз­бу­ж­де­ния в сре­де (оп­тич. и аку­стич. фо­но­ны, по­ля­ри­то­ны, ко­ле­бат., вра­щат. и элек­трон­ные воз­бу­ж­де­ния, тем­пе­ра­тур­ные вол­ны и т. д.) на раз­но­ст­ной час­то­те $Ω$ и ко­ге­рент­но рас­сеи­ва­ет­ся на них. При этом рас­се­ян­ная вол­на со сме­щён­ной в мень­шую сто­ро­ну час­то­той (сто­ксо­ва ком­по­нен­та) уси­ли­ва­ет­ся. За­ро­ж­де­ние рас­се­ян­ной вол­ны обыч­но про­ис­хо­дит за счёт спон­тан­но­го рас­сея­ния. Про­цес­сы ВРС ис­поль­зу­ют­ся для управ­ле­ния па­ра­мет­ра­ми ла­зер­но­го из­лу­че­ния: пре­об­ра­зо­ва­ния час­то­ты, дли­тель­но­сти им­пуль­сов, ко­ге­рент­но­сти. Важ­ные при­ме­не­ния на­хо­дит эф­фект об­ра­ще­ния вол­но­во­го фрон­та при ВРС. На ис­поль­зо­ва­нии вы­ну­ж­ден­ного рас­се­я­ния света ба­зи­ру­ет­ся ряд ме­то­дов не­ли­ней­ной спек­тро­ско­пии.

В сре­дах с ку­бич­еской не­ли­ней­но­стью боль­шой ин­те­рес пред­став­ля­ют эф­фек­ты са­мо­воз­дей­ст­вия све­то­вых им­пуль­сов и пуч­ков, обу­слов­лен­ные че­ты­рёх­вол­но­вы­ми взаи­мо­дей­ст­вия­ми разл. ком­по­нент их час­тот­но­го и уг­ло­во­го спек­тров. Раз­но­об­ра­зие ме­ха­низ­мов не­ли­ней­но­сти по­ка­за­те­ля пре­лом­ле­ния и воз­мож­ность эф­фек­тив­но­го управ­ле­ния про­странств. ха­рак­те­ри­сти­ка­ми про­доль­ных и по­пе­реч­ных взаи­мо­дей­ст­вий (путём варь­и­ро­вания ши­ри­ны спек­тра, ин­тен­сив­ности све­то­во­го по­ля) по­зво­ля­ют реа­ли­зо­вать в та­кой сре­де раз­но­об­раз­ные не­ли­ней­ные эф­фек­ты.

В сре­де с ве­ще­ст­вен­ным не­ли­ней­ным по­ка­за­те­лем пре­лом­ле­ния све­то­вые пуч­ки и све­то­вые им­пуль­сы ис­пы­ты­ва­ют фа­зо­вую са­мо­мо­ду­ля­цию, ко­то­рая за счёт дис­пер­сии и реф­рак­ции из­ме­ня­ет их фор­му. При рас­про­стра­не­нии в ку­бич­но-не­ли­ней­ной сре­де гар­мо­нического све­то­во­го им­пуль­са воз­ни­ка­ет за­ви­ся­щая от ин­тен­сив­но­сти до­бав­ка к фа­зе и, сле­до­ва­тель­но, час­тот­ная мо­ду­ля­ция. В ре­зуль­та­те час­тот­ный спектр им­пуль­са мо­жет силь­но уши­рять­ся. При $n_2> 0$ час­то­та уве­ли­чи­ва­ет­ся от фрон­та к хво­сту им­пуль­са. В сре­де с нор­маль­ной дис­пер­си­ей груп­по­вой ско­ро­сти это при­во­дит к бы­ст­рому рас­плы­ва­нию им­пуль­са. Ес­ли дис­пер­сия ано­маль­на, то вы­со­ко­час­тот­ные ком­по­нен­ты, груп­пи­рую­щие­ся на хво­сте им­пуль­са, до­го­ня­ют низ­ко­час­тот­ные, груп­пи­рую­щие­ся на фрон­те им­пуль­са. Вслед­ст­вие это­го им­пульс сжи­ма­ет­ся – воз­ни­ка­ет са­мо­сжа­тие, или са­мо­фо­ку­си­ров­ка во вре­ме­ни. Для фор­ми­ро­ва­ния сверх­ко­рот­ких им­пуль­сов час­то ис­поль­зу­ют­ся оп­тич. уст­рой­ст­ва, ими­ти­рую­щие дей­ст­вие сре­ды с ано­маль­ной дис­пер­си­ей, – т. н. ком­прес­со­ры. Ис­поль­зо­ва­ние тех­ни­ки уси­ле­ния им­пуль­сов с час­тот­ной мо­ду­ля­ци­ей яви­лось ос­но­вой для по­лу­че­ния мощ­ных пре­дель­но ко­рот­ких све­то­вых им­пуль­сов.

Рис. 6. Изменение профиля интенсивности светового пучка в кубично-нелинейной среде с n2>0 (вверху); штриховые линии – форма фазового фронта. Внизу показано изменение напряжённости E электриче...

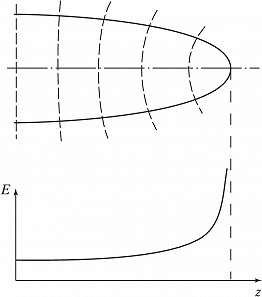
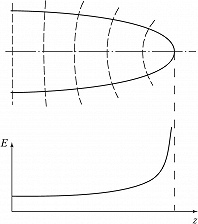
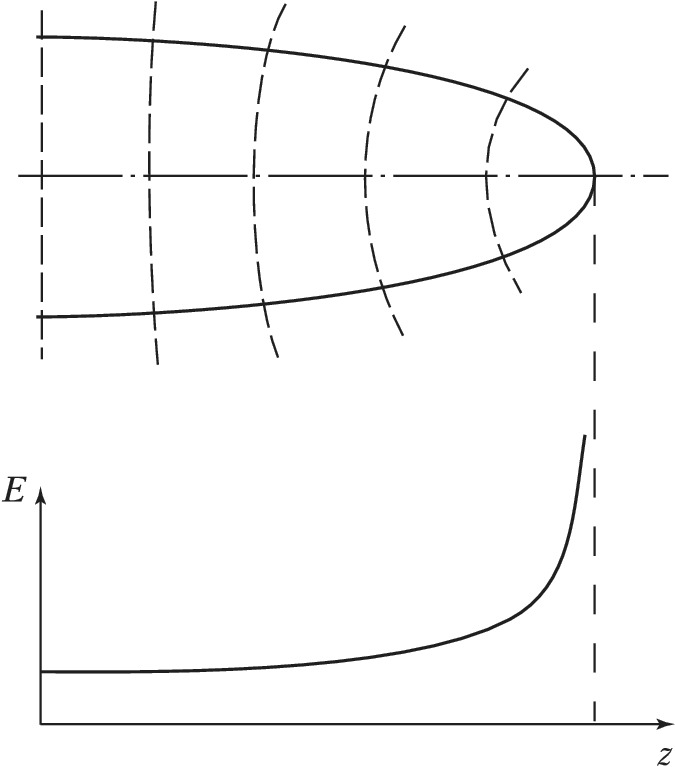
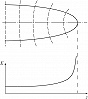
Ана­ло­гич­ные яв­ле­ния воз­ни­ка­ют при рас­про­стра­не­нии в сре­де мощ­ных све­то­вых пуч­ков. В сре­де с $n_2> 0$ (рис. 6) ко­ло­ко­ло­об­раз­ное рас­пре­де­ле­ние оги­баю­щей при­во­дит к фа­зо­вой са­мо­мо­ду­ля­ции в про­стран­ст­ве. В рас­смат­ри­вае­мом слу­чае са­мо­фо­ку­си­рую­щей сре­ды фа­зо­вая ско­рость $v_ф=c/(n_0+n_2I)$ ($c$ – ско­рость све­та) в цен­тре пуч­ка мень­ше, чем на пе­ри­фе­рии. Про­стран­ст­вен­ная фа­зо­вая са­мо­мо­ду­ля­ция уси­ли­ва­ет по­пе­реч­ную не­од­но­род­ность по­ля, ко­то­рая, в свою оче­редь, при­во­дит к уве­ли­че­нию ис­крив­ле­ния фа­зо­во­го фрон­та (не­ли­ней­ная ре­ф­рак­ция). В ре­зуль­та­те са­мо­фо­ку­си­ров­ка но­сит ла­ви­но­об­раз­ный ха­рак­тер. Одна­ко не­ли­ней­ная реф­рак­ция мо­жет сдер­жи­вать­ся ди­фрак­ци­ей. Ра­вен­ст­во эф­фек­тов не­ли­ней­ной реф­рак­ции и ди­фрак­ции дос­ти­га­ет­ся при мощ­но­сти ла­зер­но­го га­ус­со­во­го пуч­ка $P_{кр}=(1,22λ)^2c/128n_2$. При $P>P_{кр}$ не­ли­ней­ная реф­рак­ция по­дав­ля­ет ди­фрак­цию, пу­чок про­дол­жа­ет сжи­мать­ся. Пре­дел про­цес­су са­мо­фо­ку­си­ров­ки мо­жет по­ложить, напр., оп­тич. про­бой сре­ды. В са­мо­фо­ку­си­рую­щей сре­де мощ­ные ла­зер­ные пуч­ки ис­пы­ты­ва­ют т. н. мо­ду­ля­ци­он­ную не­ус­той­чи­вость, в ре­зуль­та­те ко­то­рой они раз­би­ва­ют­ся на отд. «ни­ти» (фи­ла­мен­ты).

Не­ли­ней­ная сре­да с $n_2< 0$ об­ла­да­ет са­мо­де­фо­ку­си­рую­щи­ми свой­ст­ва­ми: в ней оба эф­фек­та – ди­фрак­ция и са­мо­де­фоку­си­ров­ка – при­во­дят к рас­ши­ре­нию пуч­ка. В трёх­час­тот­ных взаи­мо­дей­ст­ви­ях мощ­ных пуч­ков в квад­ра­тич­но-не­ли­ней­ной сре­де мо­жет иметь ме­сто яв­ле­ние взаи­мо­фо­ку­си­ров­ки.

В слу­чае са­мо­сжа­тия им­пуль­са роль эф­фек­та ди­фрак­ции мо­жет вы­пол­нять дис­пер­си­он­ное рас­плы­ва­ние. При этом в ку­бич­но-нелинейной сре­де воз­мож­но фор­ми­ро­ва­ние со­ли­то­на оп­ти­че­ско­го – им­пуль­са, не из­ме­няю­ще­го свою фор­му при рас­про­стра­не­нии. Это про­ис­хо­дит при не­ко­то­рой кри­тич. плот­но­сти энер­гии им­пуль­са, за­ви­ся­щей от $n_2$, дли­тель­но­сти им­пуль­са и дис­пер­сии груп­по­вой ско­рости.

Ес­ли не­ли­ней­ная сре­да по­ме­ща­ет­ся в ре­зо­на­тор, то не­ли­ней­ные оп­тич. про­цес­сы мо­гут со­про­во­ж­дать­ся ря­дом др. яв­ле­ний: по­яв­ле­ни­ем оп­тич. гис­те­ре­зи­са, оп­ти­че­ской бис­та­биль­но­стью, ге­не­ра­ци­ей разл. дву­мер­ных струк­тур и т. д.

Эф­фек­тив­ный энер­го­об­мен ме­ж­ду взаи­мо­дей­ст­вую­щи­ми вол­на­ми в од­но­род­ных ани­зо­троп­ных кри­стал­лах мо­жет про­ис­хо­дить толь­ко при фа­зо­вом син­хро­низ­ме. Но та­кой же энер­го­об­мен воз­мо­жен и в кри­стал­лах с про­стран­ст­вен­ной мо­ду­ля­ци­ей ли­ней­ной или не­ли­ней­ной вос­при­им­чи­во­сти. Обыч­но их на­зы­ва­ют кри­стал­ла­ми с ре­гу­ляр­ной до­мен­ной струк­ту­рой. В этих кри­стал­лах фа­зо­вую рас­строй­ку вол­но­вых век­то­ров $(Δk≠0)$ мож­но ком­пен­си­ро­вать век­то­ром об­рат­ной ли­ней­ной (или не­ли­ней­ной) ре­шёт­ки, т. е. реа­ли­зо­вать ус­ло­вие ква­зи­син­хро­низ­ма. При этом вол­но­вые взаи­мо­дей­ст­вия на­зы­ва­ют ква­зи­син­хрон­ны­ми. Ус­ло­вие ква­зи­син­хро­низ­ма по­зво­ля­ет фак­ти­че­ски пре­одо­леть не­дос­тат­ки кри­стал­лов, свя­зан­ные с час­тот­ной дис­пер­си­ей.

Воз­мож­но­сти реа­ли­за­ции разл. не­ли­ней­ных взаи­мо­дей­ст­вий су­ще­ст­вен­но рас­ши­ри­лись с по­яв­ле­ни­ем фо­тон­ных кри­стал­лов и мик­ро­струк­ту­ри­ро­ван­ных све­то­во­дов. Фо­тон­ные кри­стал­лы – это сре­ды с про­стран­ст­вен­ной пе­рио­дич­но­стью оп­тич. свойств, срав­ни­мой с дли­ной све­то­вой вол­ны. Мик­ро­струк­ту­ри­ров. во­лок­на пред­став­ля­ют со­бой квар­це­вую или стек­лян­ную мик­ро­струк­ту­ру с пе­рио­дич. или апе­рио­дич. сис­те­мой ци­лин­д­рич. от­вер­стий, ори­ен­ти­ро­ван­ных вдоль оси во­лок­на. Та­кие сре­ды да­ют воз­мож­ность до­би­вать­ся эф­фек­тив­ной пе­ре­да­чи и пре­об­ра­зо­ва­ния из­лу­че­ния сверх­ко­рот­ких све­то­вых им­пуль­сов за счёт умень­ше­ния по­терь и реа­ли­за­ции фа­зо­во­го и груп­по­во­го син­хро­низ­ма для вол­но­вод­ных мод.

Но­вые воз­мож­но­сти в Н. о. от­кры­ва­ет при­ме­не­ние ме­та­ма­те­риа­лов, ко­то­рые соз­да­ют­ся из пе­рио­ди­че­ски рас­по­ло­жен­ных на­но­раз­мер­ных эле­мен­тов и мо­гут об­ла­дать от­ри­ца­тель­ны­ми ди­элек­трич. и маг­нит­ны­ми про­ни­цае­мо­стя­ми в не­ко­то­ром диа­па­зо­не длин волн. Эти осо­бен­но­сти мо­гут на­гляд­но про­явить­ся в не­ли­ней­ных оп­тич. взаи­мо­дей­ст­ви­ях, ко­гда час­то­ты взаи­мо­дей­ст­вую­щих волн ле­жат в раз­ных об­лас­тях спек­тра. В этом слу­чае воз­мож­на реа­ли­за­ция не­ли­ней­но­го взаи­мо­дей­ст­вия волн, бе­гу­щих на­встре­чу друг дру­гу.

Сильные световые поля и нелинейная оптика

Для не­ли­ней­ной оп­ти­ки ог­ром­ное зна­че­ние име­ет ге­не­ра­ция пи­ко- и фем­то­се­кунд­ных ла­зер­ных им­пуль­сов, раз­ра­бот­ка ме­то­дов их сжа­тия. При дли­тель­но­сти им­пуль­сов $τ_и≈ 1\!0^{–13}–1\!0^{–14}$ с сверх­силь­ные све­то­вые по­ля с $E⩾E_a$ мож­но по­лу­чить при энер­гии им­пуль­са 0,1 Дж. С им­пуль­са­ми дли­тель­но­стью $τ_и≈1\!0^{–8}–1\!0^{–9}$ с (ла­зе­ры с мо­ду­ли­ро­ван­ной доб­рот­но­стью) сверх­силь­ные по­ля по­лу­ча­ют толь­ко в уни­каль­ных ус­та­нов­ках с энер­ги­ей в неск. кДж, пред­на­зна­чен­ных для экс­пе­ри­мен­тов по УТС. При $E⩾E_a$ про­ис­хо­дит ра­ди­каль­ное из­ме­не­ние струк­ту­ры ве­ще­ст­ва; дис­крет­ная струк­ту­ра атом­ных уров­ней прак­ти­че­ски ис­че­за­ет, и оп­тич. от­клик оп­ре­де­ля­ет­ся пе­ре­хо­да­ми в не­пре­рыв­ном спек­тре. В дей­ст­ви­тель­но­сти это про­ис­хо­дит уже при мень­ших ин­тен­сив­но­стях волны. Кон­ден­си­ров. сре­да и не слиш­ком раз­ре­жен­ный газ ио­ни­зу­ют­ся при ин­тен­сив­но­стях $I=I_{проб}⩽I_а$. Эф­фект свя­зан с ла­вин­ным раз­мно­же­ни­ем сво­бод­ных элек­тро­нов, на­би­раю­щих энер­гию в про­цес­се столк­но­ве­ний в по­ле све­то­вой вол­ны. При дос­ти­же­нии кон­цен­тра­ции элек­тро­нов ок. $1\!0^{15}$ см^–3 воз­ни­ка­ет ла­вин­ный оп­тич. про­бой. Зна­че­ния $I_{проб}$ оп­ре­де­ля­ют­ся, преж­де все­го, со­от­но­ше­ни­ем час­то­ты све­та $ω$ и ре­зо­нанс­ной час­то­ты $ω_а$ ве­ще­ст­ва. Про­бой про­зрач­ных кри­стал­лов и стё-­кол ($ω>ω_а$, не­ре­зо­нанс­ный слу­чай) в по­ле им­пуль­сов дли­тель­но­стью $τ_и≈ 1\!0^{–8}$ с про­ис­хо­дит при ин­тен­сив­но­стях $I_{проб}≈1\!0^{11}–1\!0^{12}$ Вт/см², при $τ_и≈1\!0^{–14}$ с эта ин­тен­сив­ность увеличива­ет­ся до зна­че­ний $I_{проб}≈1\!0^{13}–1\!0^{14}$ Вт/см².

При ин­тен­сив­но­стях $I_Т< I_a$ (в не­ре­зо­нанс­ном слу­чае $I_т≈(ω/ω_а)^2I_а)$ воз­мож­ны про­яв­ле­ние тун­нель­ной ио­ни­за­ции ато­мов и ге­не­ра­ция вы­со­ких гар­мо­ник не­чёт­но­го по­ряд­ка. В бла­го­род­ных га­зах при $I_т≈1\!0^{14}–1\!0^{15}$ Вт/см 2 на­блю­да­ют­ся гар­мо­ни­ки с но­ме­ра­ми бо­лее ста. Ме­ха­низм ге­не­ра­ции та­ких гар­мо­ник не опи­сы­ва­ет­ся в рам­ках тео­рии воз­му­ще­ний и прин­ци­пи­аль­но от­ли­чен от обыч­но­го мно­го­фо­тон­но­го. При этом по­яв­ля­ет­ся воз­мож­ность по­лу­че­ния ат­то­се­кунд­ных им­пуль­сов.

Ес­ли $I⩾I_т≪I_а$, то ли­ней­ный и не­ли­ней­ный от­клики ве­ще­ст­ва оп­ре­де­ля­ют­ся фак­ти­че­ски от­кли­ком ква­зис­во­бод­ных элек­тро­нов. В све­то­вом по­ле на­пря­жён­но­стью $E=E_{рез}=mωc/e$ энер­гия ос­цил­ля­ций элек­тро­на ста­но­вит­ся срав­ни­мой с энер­ги­ей по­коя (здесь $m$ – мас­са, $e$ – за­ряд элек­тро­на); в этом слу­чае ско­рость элек­тро­на внут­ри ла­зер­но­го по­ля близ­ка к ско­ро­сти све­та $c$). Ре­ля­ти­ви­ст­ская ин­тен­сив­ность, ха­рак­те­ри­зую­щая гра­ни­цу ре­ля­ти­ви­ст­ской Н. о. сво­бод­ных элек­тро­нов, рав­на $I_{рез}=m^2ω^2c^3/4πe^2$. Для час­тот ви­ди­мо­го диа­па­зо­на $I_{рез}=1\!0^{18}$ Вт/см². В экс­пе­ри­мен­тах уже дос­тиг­ну­та ин­тен­сив­ность $I=2·1\!0^{22}$  Вт/см². При та­ких ин­тен­сив­но­стях воз­мож­но на­блю­де­ние не­ли­ней­ных том­со­нов­ско­го и ком­пто­нов­ско­го рас­сея­ний. С ис­поль­зо­ва­ни­ем экс­тре­маль­ных све­то­вых по­лей свя­зы­ва­ют на­де­ж­ды на реа­ли­за­цию эф­фек­тив­но­го ус­ко­ре­ния све­том за­ря­жен­ных час­тиц (в ча­ст­но­сти, про­то­нов) и на­блю­де­ния не­ли­ней­но­сти ва­куу­ма, ро­ж­де­ния элек­трон-по­зи­трон­ных пар (при $I∼1\!0^{29}– 1\!0^{30}$ Вт/см²).