КВА́НТОВАЯ О́ПТИКА

КВА́НТОВАЯ О́ПТИКА, раз­дел оп­ти­ки, в ко­то­ром для изу­че­ния свойств све­та и его взаи­мо­дей­ст­вия с ве­ще­ст­вом ис­поль­зу­ют прин­ци­пы кван­то­вой ме­ха­ни­ки (кор­пу­ску­ляр­но-вол­но­вой дуа­лизм, век­то­ры со­стоя­ния, пред­став­ле­ния Гей­зен­бер­га и Шрё­дин­ге­ра и т. д.).

За­ро­ж­де­ние кван­то­вой тео­рии све­та от­но­сит­ся к 1900, ко­гда М. Планк для объ­яс­не­ния спек­траль­но­го рас­пре­де­ле­ния элек­тро­маг­нит­ной энер­гии, из­лу­чае­мой те­п­ло­вым ис­точ­ни­ком, по­сту­ли­ро­вал по­гло­ще­ние и ис­пус­ка­ние её дис­крет­ны­ми пор­ция­ми. Идея дис­крет­но­сти лег­ла в ос­но­ву вы­во­да фор­му­лы, но­ся­щей его имя, и по­слу­жи­ла толч­ком для соз­да­ния кван­то­вой ме­ха­ни­ки. Од­на­ко ос­та­ва­лось не­яс­ным, яв­ля­ет­ся ли ис­точ­ни­ком дис­крет­но­сти ве­ще­ст­во или сам свет. В 1905 А. Эйн­штейн опуб­ли­ко­вал тео­рию фо­то­эф­фек­та, в ко­то­рой по­ка­зал, что его мож­но объ­яс­нить, ес­ли свет рас­смат­ри­вать как по­ток час­тиц (кван­тов све­та), на­зван­ных впо­след­ст­вии фо­то­на­ми. Фо­то­ны име­ют энер­гию $\mathscr E=h \nu$ ($h$ – по­сто­ян­ная План­ка, $\nu$  – час­то­та све­та) и рас­про­стра­ня­ют­ся со ско­ро­стью све­та. Позд­нее Н. Бор по­ка­зал, что ато­мы мо­гут ис­пус­кать свет дис­крет­ны­ми пор­ция­ми. Т. о., свет рас­смат­ри­ва­ет­ся и как элек­тро­маг­нит­ная вол­на, и как по­ток фо­то­нов. Кван­то­ван­ное све­то­вое по­ле от­но­сит­ся к ста­ти­стич. объ­ек­там, и его со­стоя­ние оп­ре­де­ля­ет­ся в ве­ро­ят­но­ст­ном смыс­ле.

Соз­да­ние в 1960 ла­зе­ра – прин­ци­пи­аль­но но­во­го ис­точ­ни­ка из­лу­че­ния по срав­не­нию с те­п­ло­вым – сти­му­ли­ро­ва­ло ис­сле­до­ва­ния ста­ти­стич. ха­рак­те­ри­стик его из­лу­че­ния. Эти ис­сле­до­ва­ния свя­за­ны с из­ме­ре­ни­ем рас­пре­де­ле­ния фо­то­нов ла­зер­но­го из­лу­че­ния и ко­ге­рент­но­сти по­ля. Не­ла­зер­ные ис­точ­ни­ки све­та яв­ля­ют­ся, по су­ще­ст­ву, ис­точ­ни­ка­ми слу­чай­ных све­то­вых по­лей с га­ус­со­вой ста­ти­сти­кой по­ля. Изу­чая ста­ти­сти­ку ла­зер­но­го из­лу­че­ния, Р. Глау­бер ввёл по­ня­тие ко­ге­рент­но­го со­стоя­ния, ко­то­ро­му хо­ро­шо со­от­вет­ст­ву­ет из­лу­че­ние ла­зе­ра, ра­бо­таю­ще­го в ре­жи­ме над по­ро­гом ге­не­ра­ции. В 1977 амер. фи­зик Дж. Кимбл впер­вые на­блю­дал т. н. ан­ти­груп­пи­ров­ку фо­то­нов (см. ни­же), ко­то­рую мож­но бы­ло объ­яс­нить с по­мо­щью кван­то­вой тео­рии.

Рис. 1. Схема измерения корреляционной функции второго порядка: ПП – светоделительная полупрозрачная пластинка; ФД-1 и ФД-2 – фотодетекторы; ПВА – преобразователь время-амплитуда, ко...

Рис. 2. Корреляционные функции второго порядка g(2)(τ) для различных излучений: теплового (1), лазерного (2) и резонансной флуоресценции (3).

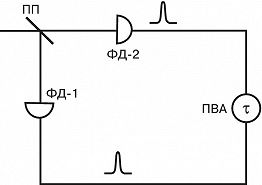
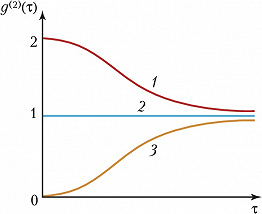
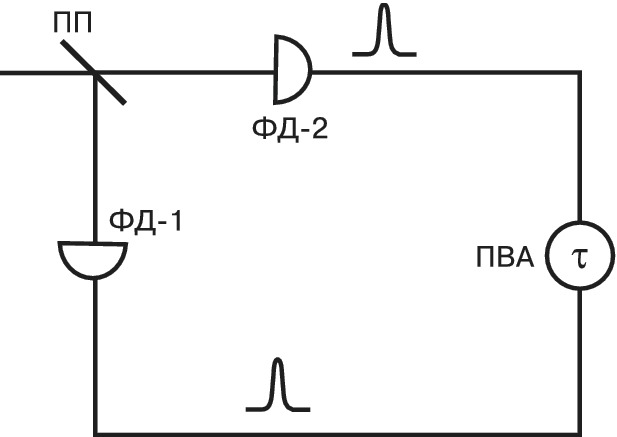
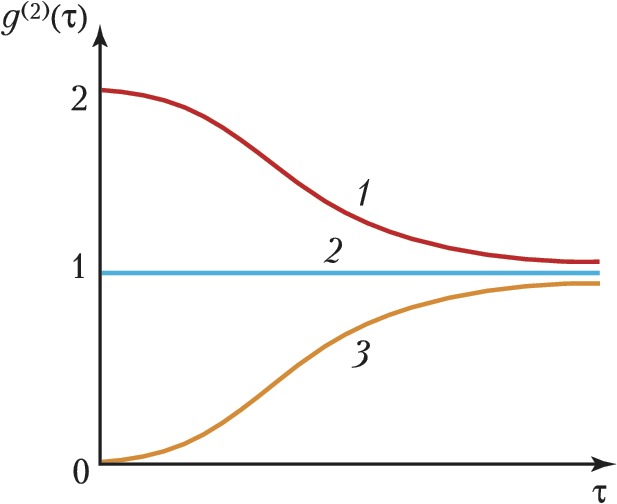
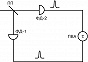
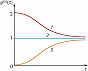
С кон. 20 в. К. о. ин­тен­сив­но раз­ви­ва­ет­ся. Она тес­но свя­за­на с не­ли­ней­ной и атом­ной оп­ти­кой, кван­то­вой тео­ри­ей ин­фор­ма­ции. Од­ним из наи­бо­лее удоб­ных спо­со­бов оп­ре­де­ле­ния со­стоя­ния све­то­во­го по­ля яв­ля­ет­ся из­ме­ре­ние кор­ре­ля­ци­он­ных функ­ций. Про­стей­шая из них – по­ле­вая кор­ре­ля­ци­он­ная функ­ция, ха­рак­те­ри­зу­ю­щая связь по­лей в разл. про­ст­ран­ст­вен­но-вре­менны́х точ­ках. Она пол­но­стью ха­рак­те­ри­зу­ет по­ле те­п­ло­во­го ис­точ­ни­ка из­лу­че­ния, од­на­ко не по­зво­ля­ет от­ли­чить ис­точ­ни­ки с др. ста­ти­стич. свой­ст­ва­ми от те­п­ло­вых. В этом от­но­ше­нии важ­ную роль иг­ра­ет кор­ре­ля­ци­он­ная функ­ция чис­ла фо­то­нов (ин­тен­сив­но­стей) вто­ро­го по­ряд­ка $g^{(2)}(\tau)$, со­дер­жа­щая све­де­ния о рас­пре­де­ле­нии вре­мён за­паз­ды­ва­ния $\tau$ ис­пус­ка­ния фо­то­нов. С её по­мо­щью из­ме­ря­ют эф­фек­ты груп­пи­ров­ки и ан­ти­груп­пи­ров­ки фо­то­нов. Свет от ис­точ­ни­ка по­сту­па­ет на све­то­де­ли­тель­ную пла­с­тин­ку (рис. 1), по­сле ко­то­рой он по­да­ёт­ся на два фо­то­де­тек­то­ра. Ре­ги­ст­ра­ция фо­то­на со­про­во­ж­да­ет­ся по­яв­ле­ни­ем им­пуль­са на вы­хо­де де­тек­то­ра. Им­пуль­сы с де­тек­то­ров по­сту­па­ют в уст­рой­ст­во, ко­то­рое из­ме­ря­ет вре­мя за­держ­ки ме­ж­ду ни­ми. Экс­пе­ри­мент по­вто­ря­ет­ся мно­го раз. Та­ким спо­со­бом из­ме­ря­ют рас­пре­де­ле­ние вре­мён за­держ­ки, ко­то­рое свя­за­но с функ­ци­ей $g^{(2)}(\tau)$. На рис. 2 изо­бра­же­на за­ви­си­мость $g^{(2)}(\tau)$ для трёх ти­пич­ных ис­точ­ни­ков све­та – те­п­ло­во­го, ла­зе­ра и ре­зо­нанс­ной флуо­рес­цен­ции. При $\tau \to \infty$ зна­че­ния функ­ций для те­п­ло­во­го ис­точ­ни­ка и ре­зо­нанс­ной флуо­рес­цен­ции при­бли­жа­ют­ся к еди­ни­це. Для ла­зер­но­го из­лу­че­ния $g^{(2)}(\tau)=1$ и ста­ти­с­ти­ка фо­то­нов пу­ас­со­нов­ская. Для те­п­ло­во­го ис­точ­ни­ка $g^{(2)}(0)=2$ и бо­лее ве­ро­ят­но об­на­ру­жить два фо­то­на при­хо­дя­щи­ми сра­зу друг за дру­гом (эф­фект груп­пи­ров­ки фо­то­нов). В слу­чае ре­зо­нанс­ной флуо­рес­цен­ции ве­ро­ят­ность ис­пус­ка­ния ато­мом сра­зу двух фо­то­нов рав­на ну­лю (ан­ти­груп­пи­ров­ка фо­то­нов). Зна­че­ние $g^{(2)}(0)=0$ обу­слов­ле­но тем, что ме­ж­ду дву­мя по­следо­ва­тель­ны­ми ак­та­ми из­лу­че­ния фо­то­нов од­ним ато­мом су­ще­ст­ву­ет вре­мя за­держ­ки. Этот эф­фект объ­яс­ня­ет­ся пол­ной кван­то­вой тео­ри­ей, ко­то­рая с кван­то­вой точ­ки зре­ния опи­сы­ва­ет и сре­ду, и элек­тро­маг­нит­ное по­ле.

С эф­фек­том ан­ти­груп­пи­ров­ки тес­но свя­за­на суб­пу­ас­со­нов­ская ста­ти­сти­ка фо­то­нов, для ко­то­рой функ­ция рас­пре­де­ле­ния ýже, чем пу­ас­со­нов­ское рас­пре­де­ле­ние. По­это­му уро­вень флук­туа­ций в фо­тон­ных пуч­ках с суб­пу­ас­со­нов­ской ста­ти­сти­кой мень­ше уров­ня флук­туа­ций ко­ге­рент­но­го излу­че­ния. В пре­дель­ном слу­чае та­кие не­клас­сич. по­ля име­ют стро­го оп­ре­де­лён­ное чис­ло фо­то­нов (т. н. фо­ков­ское со­стоя­ние по­ля). В кван­то­вой тео­рии чис­ло фо­то­нов яв­ля­ет­ся дис­крет­ной пе­ре­мен­ной.

Рис. 3. Область флуктуаций на входе (а) и выходе (б) вырожденного оптического параметрического усилителя.

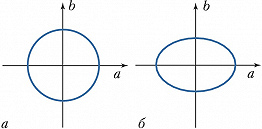
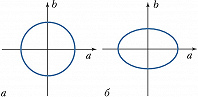
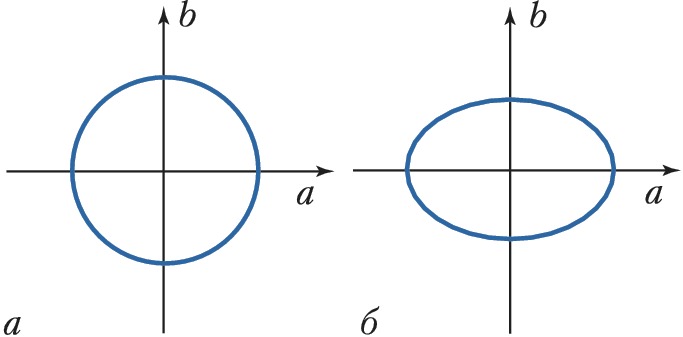
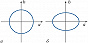
Ме­то­да­ми не­ли­ней­ной оп­ти­ки мо­гут быть соз­да­ны не­клас­сич. све­то­вые по­ля, у ко­то­рых, по срав­не­нию с ко­ге­рент­ны­ми по­ля­ми, умень­шен уро­вень кван­то­вых флук­туа­ций не­ко­то­рых не­пре­рыв­ных пе­ре­мен­ных, напр. квад­ра­тур­ных ком­по­нент или сто­ксо­вых па­ра­мет­ров, ха­рак­те­ри­зую­щих со­стоя­ние по­ля­ри­за­ции по­ля. Та­кие по­ля на­зы­ва­ют сжа­ты­ми. Ин­тер­пре­ти­ро­вать фор­ми­ро­ва­ние сжа­тых по­лей мож­но на клас­сич. язы­ке. Вы­ра­зим на­пря­жён­ность элек­трич. по­ля $E$ че­рез квад­ра­тур­ные ком­по­нен­ты $a$ и $b$: $E(t)=a(t)\cos \omega t+ b(t) \sin \omega t$, где $a(t)$ и $b(t)$ – слу­чай­ные функ­ции, $\omega=2 \pi \nu$ – кру­го­вая час­то­та, $t$ – вре­мя. При по­да­че та­ко­го по­ля на вы­ро­ж­ден­ный оп­тич. па­ра­мет­рич. уси­ли­тель (ВОПУ) с час­то­той на­кач­ки $2 \omega$ од­на квад­ра­тур­ная ком­по­нен­та (напр., $a$) мо­жет уси­ли­вать­ся бла­го­да­ря его фа­зо­вой чув­ст­ви­тель­но­сти, а др. квад­ра­ту­ра ($b$) по­дав­лять­ся. Вслед­ст­вие это­го флук­туа­ции в квад­ра­ту­ре $a$ воз­рас­та­ют, а в квад­ра­ту­ре $b$ умень­ша­ют­ся. Транс­фор­ма­ция уров­ня шу­ма в ВОПУ изо­бра­же­на на рис. 3. На рис. 3, б об­ласть флук­туа­ций по срав­не­нию с вход­ным со­стоя­ни­ем (рис. 3, а) сжа­та. По­доб­ным об­ра­зом ве­дут се­бя при па­ра­мет­рич. уси­ле­нии кван­то­вые флук­туа­ции ва­ку­ум­но­го и ко­ге­рент­но­го со­стоя­ний. Ко­неч­но, в этом слу­чае кван­то­во­ме­ха­нич. со­от­но­ше­ние не­оп­ре­де­лён­но­стей не на­ру­ша­ет­ся (про­ис­хо­дит как бы пе­ре­рас­пре­де­ле­ние флук­туа­ций ме­ж­ду квад­ра­ту­ра­ми). В па­ра­мет­рич. про­цес­сах фор­ми­ру­ет­ся, как пра­ви­ло, из­лу­че­ние с су­пер­пу­ас­со­нов­ской ста­ти­сти­кой фо­то­нов, для ко­то­рой уро­вень флук­туа­ций пре­вы­ша­ет та­ко­вой для ко­ге­рент­но­го све­та.

Для ре­ги­ст­ра­ции сжа­тых по­лей ис­поль­зу­ют ба­ланс­ные го­мо­дин­ные де­тек­то­ры, ко­то­рые мо­гут ре­ги­ст­ри­ро­вать лишь од­ну квад­ра­ту­ру. Т. о., уро­вень флук­туа­ций при фо­то­де­тек­ти­ро­ва­нии сжа­то­го све­та мо­жет быть ни­же уров­ня стан­дарт­но­го кван­то­во­го пре­де­ла (дро­бо­во­го шу­ма), со­от­вет­ст­вую­ще­го ре­ги­ст­ра­ции ко­ге­рент­но­го све­та. В сжа­том све­те флук­туа­ции мо­гут быть по­дав­ле­ны до 90% по от­но­ше­нию к ко­ге­рент­но­му со­стоя­нию. Ме­то­да­ми не­ли­ней­ной оп­ти­ки по­лу­ча­ют так­же по­ля­ри­за­ци­он­но-сжа­тый свет, в ко­то­ром по­дав­ле­ны флук­туа­ции по край­ней ме­ре в од­ном из сто­ксо­вых па­ра­мет­ров. Сжа­тый свет пред­став­ля­ет ин­те­рес для пре­ци­зи­он­ных оп­ти­ко-фи­зич. экс­пе­ри­мен­тов, в ча­ст­но­сти для ре­ги­ст­ра­ции гра­ви­тац. волн.

С кван­то­вой точ­ки зре­ния рас­смот­рен­ный па­ра­мет­рич. про­цесс пред­став­ля­ет со­бой про­цесс рас­па­да фо­то­на на­кач­ки с час­то­той $2 \omega$ на два фо­то­на с час­то­той $\omega$. Ина­че го­во­ря, фо­то­ны в сжа­том све­те соз­да­ют­ся пáрами (би­фо­то­ны), и функ­ция их рас­пре­де­ле­ния ра­ди­каль­но от­ли­ча­ет­ся от пу­ас­со­нов­ской (име­ет­ся толь­ко чёт­ное чис­ло фо­то­нов). Это дру­гое не­обыч­ное свой­ст­во сжа­то­го све­та на язы­ке дис­крет­ных пе­ре­мен­ных.

Ес­ли фо­то­ны на­кач­ки в па­ра­мет­рич. про­цес­се рас­па­да­ют­ся на два фо­то­на, ко­то­рые раз­ли­ча­ют­ся час­то­та­ми и/или по­ля­ри­за­ция­ми, то та­кие фо­то­ны кор­ре­ли­ро­ва­ны (свя­за­ны) ме­ж­ду со­бой. Обо­зна­чим час­то­ты ро­див­ших­ся фо­то­нов как $\omega_1$ и $\omega_2$, и пусть фо­то­ны име­ют со­от­вет­ст­вен­но вер­ти­каль­ную ($V$) и го­ри­зон­таль­ную ($H$) по­ля­ри­за­ции. Со­стоя­ние по­ля в этом слу­чае на кван­то­вом язы­ке за­пи­сы­ва­ет­ся в ви­де $|\psi \rangle=|V \rangle_1|H\rangle_2$. Ока­зы­ва­ет­ся, что при оп­ре­де­лён­ной ори­ен­та­ции не­ли­ней­но-оп­тич. кри­стал­ла, в ко­то­ром на­блю­да­ет­ся па­ра­мет­рич. про­цесс, фо­то­ны той же час­то­ты, рас­про­стра­няю­щие­ся в том же на­прав­ле­нии, мо­гут рож­дать­ся с ор­то­го­наль­ны­ми по­ля­ри­за­ция­ми. В ре­зуль­та­те со­стоя­ние по­ля при­ни­ма­ет вид: $$|\psi \rangle=\frac{1}{\sqrt 2}(|V\rangle_1|H \rangle_2+|H\rangle_1|V\rangle_2). \quad\tag{*}$$(По­яв­ле­ние ко­эф. пе­ред скоб­кой свя­за­но с ус­ло­ви­ем нор­ми­ров­ки.)

Со­стоя­ние фо­то­нов, опи­сы­вае­мое со­от­но­ше­ни­ем (*), на­зы­ва­ют пе­ре­пу­тан­ным; это оз­на­ча­ет, что ес­ли фо­тон час­то­ты $\omega_1$ по­ля­ри­зо­ван вер­ти­каль­но, то фо­тон час­то­ты $\omega_2$ – го­ри­зон­таль­но, и на­обо­рот. Важ­ное свой­ст­во пе­ре­пу­тан­но­го со­стоя­ния (*) за­клю­ча­ет­ся в том, что из­ме­ре­ние со­стоя­ния по­ля­ри­за­ции од­но­го фо­то­на про­ек­ти­ру­ет со­стоя­ние фо­то­на др. час­то­ты в ор­то­го­наль­ное. Со­стоя­ния ти­па (*) на­зы­ва­ют так­же пáрами Эйн­штей­на – По­доль­ско­го – Ро­зе­на и пе­ре­пу­тан­ны­ми со­стоя­ния­ми Бел­ла. В пе­ре­пу­тан­ном со­стоя­нии мо­гут на­хо­дить­ся кван­то­вые со­стоя­ния атом­ных сис­тем, а так­же со­стоя­ния ато­мов и фо­то­нов. С при­ме­не­ни­ем фо­то­нов в пе­ре­пу­тан­ных со­стоя­ни­ях про­ве­де­ны экс­пе­ри­мен­ты по про­вер­ке не­ра­вен­ст­ва Бел­ла, кван­то­вая те­ле­пор­та­ция и кван­то­вое плот­ное ко­ди­ро­ва­ние.

На ос­но­ве па­ра­мет­рич. оп­тич. взаи­мо­дей­ст­вий, а так­же эф­фек­та кросс-взаи­мо­дей­ст­вий осу­ще­ст­в­ле­ны кван­то­вые не­раз­ру­шаю­щие из­ме­ре­ния со­от­вет­ст­вен­но квад­ра­тур­ных ком­по­нент и чис­ла фо­то­нов. При­ме­не­ние ме­то­дов К. о. при об­ра­бот­ке оп­тич. изо­бра­же­ний по­зво­ля­ет улуч­шить их за­пись, хра­не­ние и счи­ты­ва­ние (см. Кван­то­вая об­ра­бот­ка изо­б­ра­же­ний).

Кван­то­вые флук­туа­ции элек­тро­маг­нит­но­го по­ля в ва­ку­ум­ном со­стоя­нии мо­гут про­яв­лять­ся свое­об­раз­но: они при­во­дят к воз­ник­но­ве­нию си­лы при­тя­же­ния меж­ду про­во­дя­щи­ми не­за­ря­жен­ны­ми плас­ти­на­ми (см. Ка­зи­ми­ра эф­фект).

К К. о. от­но­сят и тео­рию флук­туа­ций ла­зер­но­го из­лу­че­ния. Её по­сле­до­ва­тель­ная раз­ра­бот­ка ба­зи­ру­ет­ся на кван­то­вой тео­рии, ко­то­рая да­ёт кор­рект­ные ре­зуль­та­ты для ста­ти­сти­ки фо­то­нов и ши­ри­ны ли­нии ла­зер­но­го из­лу­че­ния.

К. о. за­ни­ма­ет­ся так­же ис­сле­до­ва­ния­ми взаи­мо­дей­ст­вия ато­мов со све­то­вым по­лем, воз­дей­ст­вия све­та на двух- и трёх­уров­не­вые ато­мы. При этом об­на­ру­жен ряд ин­те­рес­ных и не­ожи­дан­ных эф­фек­тов, свя­зан­ных с атом­ной ко­ге­рент­но­стью: кван­то­вые бие­ния (см. Ин­тер­фе­рен­ция со­стоя­ний), Хан­ле эф­фект, фо­тон­ное эхо и др.

В К. о. изу­ча­ют так­же ох­ла­ж­де­ние ато­мов при взаи­мо­дей­ст­вии со све­том и по­лу­че­ние бо­зе-эйн­штей­нов­ско­го кон­ден­са­та, а так­же ме­ха­нич. воз­дей­ст­вие све­та на ато­мы с це­лью их за­хва­та и управ­ле­ния.