НЕЛИНЕ́ЙНАЯ СПЕКТРОСКОПИ́Я

НЕЛИНЕ́ЙНАЯ СПЕКТРОСКОПИ́Я, со­во­куп­ность ме­то­дов оп­тич. спек­тро­ско­пии, в ко­то­рых ин­фор­ма­цию о строе­нии ве­ще­ст­ва и о про­цес­сах в нём по­лу­ча­ют с по­мо­щью не­ли­ней­ных оп­тич. эф­фек­тов. Н. с. при­над­ле­жит к ла­зер­ной спек­тро­ско­пии, по­сколь­ку для на­блю­де­ния и ис­сле­до­ва­ния не­ли­ней­ных яв­ле­ний не­об­хо­ди­мо оп­тич. из­лу­че­ние вы­со­кой ин­тен­сив­но­сти, по­лу­чае­мое толь­ко с по­мо­щью ла­зе­ров. Пер­вые ра­бо­ты по Н. с. поя­ви­лись в 1964–66, од­на­ко ре­гу­ляр­ные ис­сле­до­ва­ния в этом на­прав­ле­нии на­ча­лись лишь по­сле соз­да­ния ла­зер­ных ис­точ­ников уз­ко­по­лос­но­го из­лу­че­ния с плав­но пе­ре­страи­вае­мой час­то­той, ла­зе­ров, ге­не­ри­рую­щих све­то­вые им­пуль­сы пи­ко- и фем­то­се­кунд­ной дли­тель­но­сти, и др. ла­зер­ных уст­ройств со ста­биль­ны­ми, хо­ро­шо управ­ляе­мы­ми па­ра­мет­ра­ми из­лу­че­ния.

Ме­то­ды Н. с. ос­но­ва­ны на ис­сле­до­ва­нии за­ви­си­мо­сти не­ли­ней­ных яв­ле­ний от час­то­ты из­лу­че­ния, его ин­тен­сив­но­сти, по­ля­ри­за­ции, на­прав­ле­ния рас­про­стра­не­ния, вре­менны́х ха­рак­те­ри­стик и др. На­ря­ду с прин­ци­пи­аль­но но­вой ин­фор­ма­ци­ей, ме­то­ды Н. с. по­зво­ля­ют по­лу­чать так­же дан­ные, дос­туп­ные ли­ней­ной спек­тро­ско­пии, но час­то с су­ще­ст­вен­но боль­шей точ­но­стью, бо­лее вы­со­ким час­тот­ным и про­стран­ст­вен­ным раз­ре­ше­ни­ем, бо­лее вы­со­ким от­но­ше­ни­ем сиг­на­ла к шу­му и т. п.

Важ­ным свой­ст­вом Н. с. яв­ля­ет­ся вы­со­кое и сверх­вы­со­кое раз­ре­ше­ние атом­ных и мо­ле­ку­ляр­ных спек­тров. В га­зах при от­но­си­тель­но низ­ком дав­ле­нии ато­мы и мо­ле­ку­лы ис­пус­ка­ют и по­гло­ща­ют свет на час­то­тах, сме­щён­ных из-за До­п­ле­ра эф­фек­та от­но­си­тель­но собств. час­тот не­под­виж­ных час­тиц в ли­ней­ном при­бли­же­нии на ве­ли­чи­ну $Δω_D=±kv$, где $k$ – вол­но­вой век­тор све­то­вой вол­ны, $v$ – ско­рость дви­же­ния час­ти­цы, зна­ки «+» и «–» от­но­сят­ся к ис­пус­ка­нию и по­гло­ще­нию со­от­вет­ст­вен­но. Ли­нии по­гло­ще­ния и ис­пус­ка­ния ан­самб­ля хао­ти­че­ски дви­жу­щих­ся (те­п­ло­вое дви­же­ние) час­тиц со­сто­ят из мно­же­ст­ва близ­ких ли­ний, ха­рак­тер­ных для отд. час­тиц, имею­щих оп­ре­де­лён­ную ско­рость. Эти ли­нии пе­ре­кры­ва­ют­ся, об­ра­зуя ши­ро­кую ли­нию (не­од­но­род­ное уши­ре­ние). Ин­фор­ма­ция об ис­тин­ной ши­ри­не ли­ний отд. час­тиц (од­но­род­ная ши­ри­на) ока­зы­ва­ет­ся за­мас­ки­ро­ван­ной не­од­но­род­ным уши­ре­ни­ем. Кро­ме то­го, спек­траль­ные ли­нии отд. ато­мов и мо­ле­кул мо­гут иметь несколько близ­ко рас­по­ло­жен­ных ком­по­нент. Ес­ли рас­стоя­ние ме­ж­ду ком­по­нен­та­ми $Δω$ мень­ше до­п­ле­ров­ской ши­ри­ны $γ_D$, то струк­ту­ра ли­нии в обыч­ных (ли­ней­ных) спек­трах из­лу­че­ния и по­гло­ще­ния не про­яв­ля­ет­ся, т. е. те­ря­ет­ся ин­фор­ма­ция о тон­кой и сверх­тон­кой струк­ту­рах кван­то­вых уров­ней ато­мов и мо­ле­кул, об их сдви­гах и рас­ще­п­ле­нии во внеш­них по­лях.

В твёр­дых те­лах не­од­но­род­ное уши­ре­ние для при­мес­ных ато­мов мо­жет быть свя­за­но с тем, что ка­ж­дый атом на­хо­дит­ся в оп­ре­де­лён­ном ло­каль­ном элек­трич. по­ле, ко­то­рое вы­зы­ва­ет сдвиг кван­то­вых уров­ней (Штар­ка эф­фект). Слу­чай­ные раз­ли­чия ло­каль­ных по­лей в раз­ных точ­ках сре­ды обу­слов­ли­ва­ют не­од­но­род­ное уши­ре­ние спек­траль­ных ли­ний, с ко­то­рым свя­за­ны прак­ти­че­ски те же слож­но­сти, что и в слу­чае до­п­ле­ров­ско­го уши­ре­ния.

Рис. 1. Тонкая структура линии Hα серии Бальмера для атома водорода, разрешённая с помощью спектроскопии насыщения.

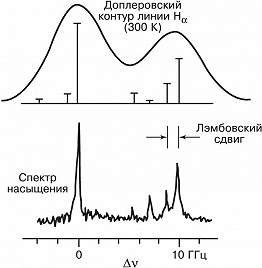
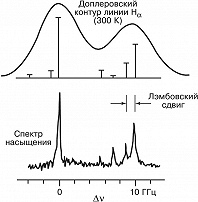
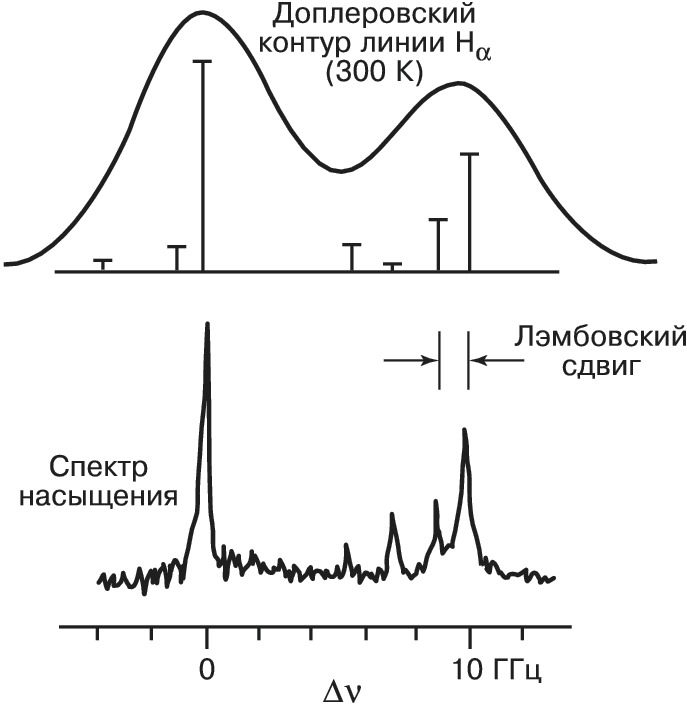
Уст­ра­нить или су­ще­ст­вен­но умень­шить влия­ние не­од­но­род­но­го уши­ре­ния по­зво­ля­ет ме­тод спек­тро­ско­пии на­сы­ще­ния. В этом ме­то­де на сре­ду по­да­ётся мощ­ное мо­но­хро­ма­тич. ла­зер­ное из­лу­че­ние (из­лу­че­ние на­кач­ки), вы­зы­ваю­щее пе­ре­рас­пре­де­ле­ние на­се­лён­но­стей ре­зо­нанс­ных кван­то­вых уров­ней (см. На­сы­ще­ния эф­фект). Наи­бо­лее зна­чи­тель­ным эф­фект на­сы­ще­ния ока­зы­ва­ет­ся для той груп­пы час­тиц, ре­зонанс­ная час­то­та ко­то­рых сов­па­да­ет с час­то­той на­кач­ки. Вы­явить из­ме­не­ния в по­гло­ще­нии (или в пре­лом­ле­нии), вы­зван­ные дей­ст­ви­ем на­кач­ки, мож­но, на­пра­вив в сре­ду встреч­ный пу­чок сла­бо­го (проб­но­го) из­лу­че­ния, пе­ре­страи­вае­мо­го по час­то­те. Ес­ли уши­ре­ние до­п­ле­ров­ское (ато­мар­ный или мо­ле­ку­ляр­ный газ), то в ка­чест­ве проб­но­го из­лу­че­ния ис­поль­зу­ют не­боль­шую часть пуч­ка на­кач­ки, от­ветв­ляе­мую с по­мо­щью зер­кал. Ска­ни­ро­ва­ние час­то­ты из­лу­че­ния при­во­дит к то­му, что в спек­тре по­гло­ще­ния проб­но­го пуч­ка воз­ни­ка­ет про­вал с цен­тром на собств. час­то­те кван­то­во­го пе­ре­хо­да, ши­ри­на ко­то­ро­го прак­ти­че­ски сов­па­да­ет с од­но­род­ной ши­ри­ной ли­нии. Ес­ли в пре­де­лах до­п­ле­ров­ской ли­нии име­ет­ся неск. спек­траль­ных ком­по­нент, то в спек­тре на­сы­ще­ния они бу­дут раз­ре­ше­ны (рис. 1). При­ме­не­ние спек­тро­ско­пии на­сы­ще­ния к ато­мам во­до­ро­да и во­до­ро­до­по­доб­ным ио­нам по­зво­ли­ло впер­вые на­блю­дать оп­тич. ме­то­да­ми лэм­бов­ский сдвиг уров­ней, а так­же по­лу­чить зна­че­ние по­сто­ян­ной Рид­бер­га, на 2 по­ряд­ка бо­лее точ­ное. Эти ре­зуль­та­ты име­ют су­ще­ст­вен­ное зна­че­ние для фун­дам. фи­зи­ки.

При ис­поль­зо­ва­нии спек­тро­ско­пии на­сы­ще­ния для твёр­дых тел не­об­хо­ди­мо, что­бы час­то­та проб­но­го пуч­ка из­ме­ня­лась не­за­ви­си­мо от час­то­ты на­кач­ки, т. е. тре­бу­ет­ся до­пол­нит. ла­зер. При этом ши­ри­на ре­зо­нан­сов на­сы­ще­ния со­от­вет­ст­ву­ет од­но­род­ной ши­ри­не ли­нии, а час­то­та ре­зо­нан­сов сов­па­да­ет с час­то­той на­кач­ки.

Рис. 2. а – Принцип двухфотонной спектроскопии, свободной от доплеровского уширения; б – доплеровски уширенный спектр двухфотонного перехода 3s–5s в атомах натрия, возбуждаемых одним...

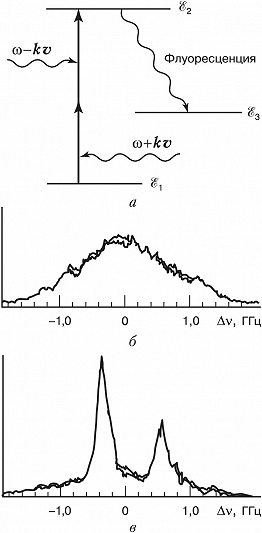
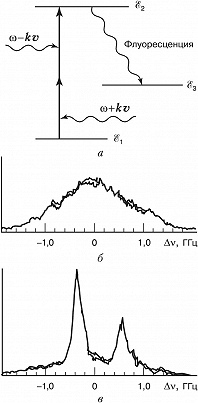
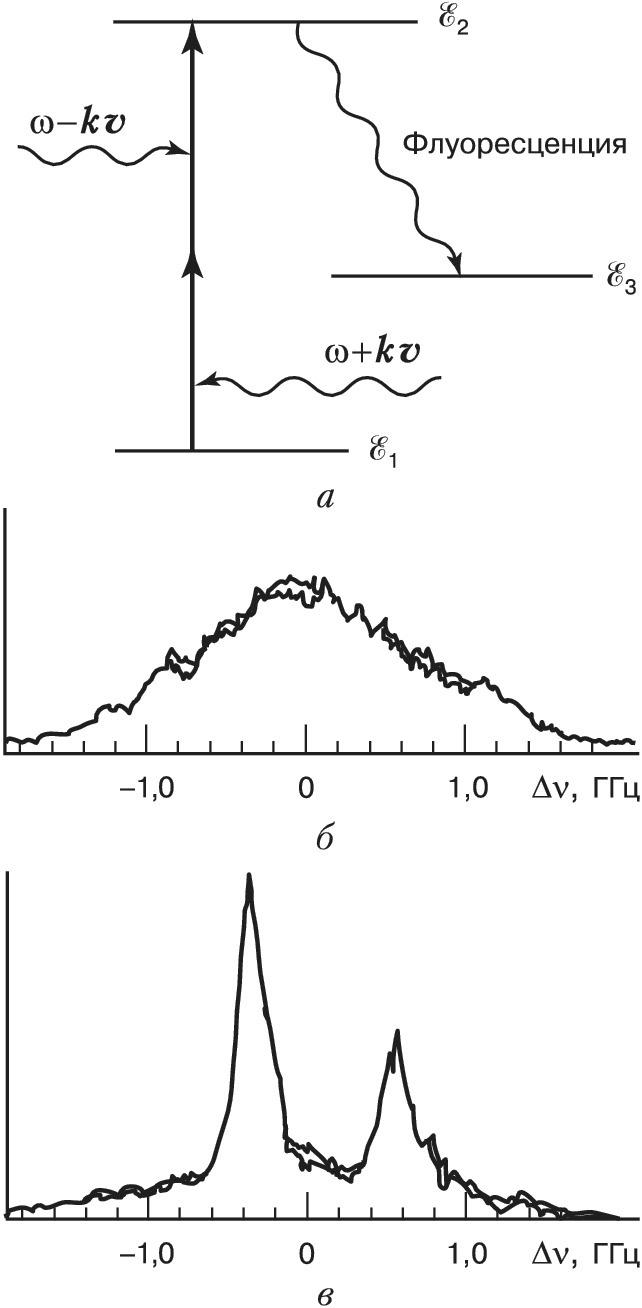
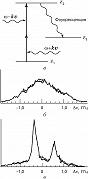
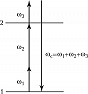
Уст­ра­нить до­п­ле­ров­ское уши­ре­ние мож­но ме­то­дом спек­тро­ско­пии двух­фо­тон­но­го по­гло­ще­ния. Пусть ато­мар­ный (или мо­ле­ку­ляр­ный) газ об­лу­ча­ет­ся дву­мя ла­зер­ны­ми пуч­ка­ми оди­на­ко­вой час­то­ты $ω$, рас­про­стра­няю­щи­ми­ся на­встре­чу друг дру­гу и спо­соб­ны­ми инду­ци­ро­вать двух­фо­тон­ные пе­ре­хо­ды с уров­ня энергии $ℰ_1$ на уро­вень $ℰ_2$ (рис. 2, а), $2ω≈ω_{21}$, где $ω_{21}=(ℰ2-ℰ1)/ℏ$ – час­то­та пе­ре­хо­да в не­под­виж­ном ато­ме, $ℏ$ – по­сто­ян­ная План­ка. То­гда для про­цес­сов, в ко­то­рых один фо­тон бе­рёт­ся из пуч­ка с вол­но­вым век­то­ром $k$, а др. фо­тон – из встреч­но­го пуч­ка с вол­но­вым век­то­ром $–k$, все ато­мы, не­за­ви­си­мо от их ско­ро­стей, бу­дут ре­зо­нанс­ны­ми. По­это­му сиг­нал двух­фо­тон­но­го по­гло­ще­ния, воз­ни­каю­щий при ска­ни­ро­ва­нии час­то­ты из­лу­че­ния, бу­дет иметь вид уз­ко­го ре­зо­нанс­но­го пи­ка (с цен­тром при $2ω≈ω_{21}$), сво­бод­но­го от до­п­ле­ров­ско­го уши­ре­ния (рис. 2, б, в). Этот ме­тод по­зво­ля­ет по­лу­чать вы­со­кое раз­ре­ше­ние при изу­че­нии вы­со­ко­ле­жа­щих уров­ней энер­гии, пе­ре­хо­ды на ко­то­рые до­пус­ка­ют­ся пра­ви­ла­ми от­бо­ра.

Спек­тро­ско­пия двух­фо­тон­но­го по­гло­ще­ния яв­ля­ет­ся ча­ст­ным слу­ча­ем ме­то­да спек­тро­ско­пии мно­го­фо­тон­но­го воз­бу­ж­де­ния, в ос­но­ве ко­то­ро­го ле­жит ис­поль­зо­ва­ние мно­го­фо­тон­ных пе­ре­хо­дов из осн. со­стоя­ния в воз­бу­ж­дён­ные. Сиг­на­лом пе­ре­хо­да в воз­бу­ж­дён­ное со­стоя­ние, как пра­ви­ло, яв­ля­ет­ся из­лу­че­ние лю­ми­нес­цен­ции на об­рат­ных пе­ре­хо­дах с воз­бу­ж­дён­ных уровней на бо­лее низ­кие уров­ни. Ши­ро­ко ис­поль­зу­ет­ся так­же ре­ги­ст­ра­ция фо­то­элек­тро­нов, воз­ни­каю­щих при фо­то­ио­ни­за­ции ато­мов и мо­ле­кул с воз­бу­ж­дён­но­го уров­ня. При этом воз­мож­но по­лу­че­ние спек­тров, сво­бод­ных от до­п­ле­ров­ско­го уши­ре­ния.

Рис. 3. Генерация сигнала на суммарной частоте в условиях двухфотонного резонанса при четырёхфотонном смешении; 1, 2 – уровни энергии.

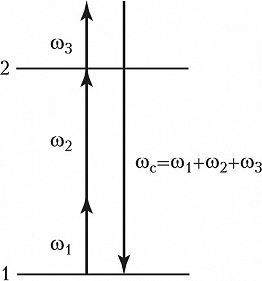
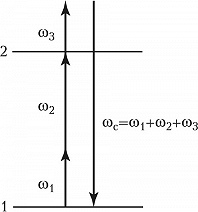
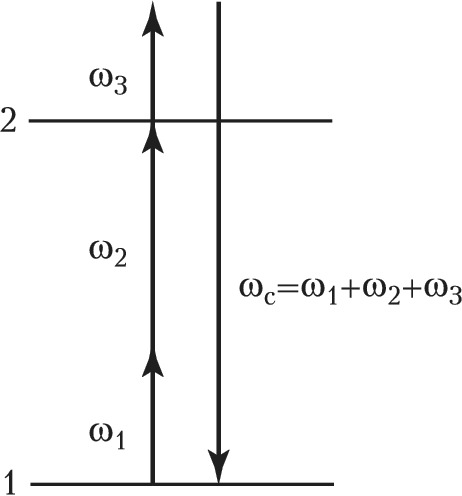
Ши­ро­кий круг за­дач ре­ша­ет­ся ме­то­да­ми, ос­но­ван­ны­ми на на­блю­де­нии па­ра­мет­рич. про­цес­сов мно­го­вол­но­во­го (мно­го­фо­тон­но­го) сме­ше­ния. Па­ра­мет­ри­че­ски­ми обыч­но на­зы­ва­ют про­цес­сы, при ко­то­рых в ка­ж­дом эле­мен­тар­ном ак­те взаи­мо­дей­ст­вия фо­то­нов ко­неч­ное со­стоя­ние сре­ды сов­па­да­ет с на­чаль­ным. В Н. с. час­то ис­поль­зу­ются про­цес­сы че­ты­рёх­вол­но­во­го сме­ше­ния, обу­слов­лен­ные не­ли­ней­ной вос­при­им­чи­во­стью 3-го по­ряд­ка $χ^{(3)}(ωc; ω_1±ω_2, ±ω_3)$, где $ω_c=ω_1±ω_2±ω_3$ – час­то­та сиг­наль­ной вол­ны, ге­не­ри­руе­мой в ис­сле­дуе­мой сре­де под дей­ст­ви­ем волн на­кач­ки на час­то­тах $ω_1, ω_2, ω_3$ (рис. 3).

Эти­ми ме­то­да­ми ре­ги­ст­ри­ру­ет­ся час­тот­ная за­ви­си­мость ин­тен­сив­но­сти (или по­ля­ри­за­ции) сиг­наль­ной све­то­вой вол­ны. Ко­гда час­то­та хо­тя бы од­ной из волн на­кач­ки или ли­ней­ная ком­би­на­ция час­тот ти­па $2ω_1, ω_1±ω_2$ и т. п. ока­зы­ва­ет­ся вбли­зи час­то­ты со­от­вет­ст­вую­ще­го раз­ре­шён­но­го кван­то­во­го пе­ре­хо­да, то в за­ви­си­мо­сти сиг­на­ла от час­то­ты про­яв­ля­ют­ся ре­зо­нанс­ные из­ме­не­ния, со­дер­жа­щие не­об­хо­ди­мую спек­тро­ско­пич. ин­фор­ма­цию. При этом с по­мо­щью све­то­вых пуч­ков, час­то­ты ко­то­рых ле­жат в ви­ди­мом диа­па­зо­не в об­лас­ти про­зрач­но­сти сре­ды, мож­но по­лу­чать ин­фор­ма­цию о ре­зо­нан­сах и дис­пер­си­он­ных свой­ст­вах ве­ще­ст­ва в ИК- и УФ-диа­па­зо­нах. По­сколь­ку наи­бо­лее эф­фек­тив­ная ге­не­ра­ция сиг­наль­ной вол­ны в па­ра­мет­рич. про­цес­се про­ис­хо­дит в на­прав­ле­нии фа­зо­во­го син­хро­низ­ма $k_c=k_1±k_2±k_3$, мож­но чёт­ко вы­де­лить на­прав­ле­ние рас­про­стра­не­ния ко­ге­рент­но­го сиг­на­ла и от­де­лить сиг­нал от фо­но­вой за­свет­ки.

Час­то воз­ник­но­ве­ние сиг­наль­ной вол­ны в спек­тро­ско­пии сме­ше­ния мож­но трак­то­вать как ко­ге­рент­ное ан­ти­сто­ксо­во рас­сея­ние од­ной из све­то­вых волн на вол­не воз­бу­ж­де­ния, по­ро­ж­дён­ной др. вол­на­ми. По­это­му ме­тод мно­го­вол­но­во­го сме­ше­ния на­зы­ва­ют так­же спек­тро­ско­пи­ей ко­ге­рент­но­го ан­ти­сто­ксо­ва рас­сея­ния све­та (КАРС-спек­тро­ско­пия).

Н. с. с вре­менны́м раз­ре­ше­ни­ем ос­но­ва­на на на­блю­де­нии не­ста­цио­нар­ных не­ли­ней­ных про­цес­сов, та­ких как за­ту­ха­ние сво­бод­ной по­ля­ри­за­ции, фо­тон­ное (све­то­вое) эхо, не­ста­цио­нар­ные про­цес­сы мно­го­вол­но­во­го сме­ше­ния и др.

За­ту­ха­ние сво­бод­ной по­ля­ри­за­ции – это умень­ше­ние ам­пли­ту­ды по­ля­ри­за­ции сре­ды по­сле пре­кра­ще­ния дей­ст­вия воз­бу­ж­даю­ще­го им­пуль­са ре­зо­нанс­но­го из­лу­че­ния, обу­слов­лен­ное ре­лак­са­ци­он­ны­ми про­цес­са­ми. Па­даю­щий на сре­ду им­пульс ко­ге­рент­но­го элек­тро­маг­нит­но­го из­лу­че­ния с час­то­той $ω$, ре­зо­нанс­ной раз­ре­шён­но­му кван­то­во­му пе­ре­хо­ду ме­ж­ду уров­ня­ми энер­гии отд. кван­то­вых сис­тем (ато­мов, мо­ле­кул, при­мес­ных цен­тров и т. д.), ин­ду­ци­ру­ет эле­мен­тар­ные ди­по­ли, ко­леб­лю­щие­ся с час­то­той по­ля и свя­зан­ные ме­ж­ду со­бой по фа­зе. В ре­зуль­та­те об­ра­зу­ет­ся вол­на по­ля­ри­за­ции ве­ще­ст­ва, ко­леб­лю­щая­ся с час­то­той $ω$. По окон­ча­нии им­пуль­са, ко­гда сре­да сво­бод­на от воз­дей­ст­вия внеш­не­го по­ля, ре­зо­нанс­ная по­ля­ри­за­ция ещё со­хра­ня­ет­ся, од­на­ко её ам­пли­ту­да со вре­ме­нем умень­ша­ет­ся, а элек­тро­маг­нит­ная вол­на, по­ро­ж­дён­ная за­ту­хаю­щей вол­ной по­ля­ри­за­ции, ре­ги­ст­ри­ру­ет­ся как сиг­нал за­ту­ха­ния сво­бод­ной по­ля­ри­за­ции. Умень­ше­ние ам­пли­ту­ды вол­ны по­ля­ри­за­ции свя­за­но, во-пер­вых, с про­цес­са­ми не­об­ра­ти­мой ре­лак­са­ции, при­во­дя­щи­ми к за­ту­ха­нию ко­ле­ба­ний отд. ди­по­лей за вре­мя т. н. по­пе­реч­ной ре­лак­са­ции $T_2^*$. Во-вто­рых, при на­ли­чии не­од­но­род­но­го уши­ре­ния ли­нии пе­ре­хо­да отд. ди­по­ли в сво­бод­ном со­стоя­нии ко­леб­лют­ся с разл. час­то­та­ми, и воз­ни­каю­щая рас­фа­зи­ров­ка отд. из­лу­ча­те­лей ве­дёт к умень­ше­нию ам­пли­ту­ды вол­ны по­ля­ри­за­ции, не свя­зан­но­му с по­те­рей энер­гии ко­ле­ба­ний эле­мен­тар­ных ди­по­лей. Этот про­цесс ха­рак­те­ри­зу­ет­ся вре­ме­нем об­ра­ти­мой ре­лак­са­ции , ко­то­рое оп­ре­де­ля­ет­ся не­од­нород­ной ши­ри­ной ли­нии $Δω_n: T_2^*= Δω_n^{-1}$.

На­блю­де­ние сиг­на­ла за­ту­ха­ния сво­бод­ной по­ля­ри­за­ции по­зво­ля­ет непо­сред­ственно оп­ре­де­лить вре­мя по­пе­реч­ной ре­лак­са­ции. Ес­ли од­но­вре­мен­но воз­бу­ж­да­ют­ся близ­кие по час­то­те кван­то­вые пе­ре­хо­ды, то во вре­менно́м по­ве­де­нии сиг­на­ла по­яв­ля­ют­ся ос­цил­ля­ции, по ко­то­рым мож­но оп­ре­де­лить раз­ность час­тот пе­ре­хо­дов.

Ши­ро­ко ис­поль­зу­ет­ся в Н. с. эф­фект фо­тон­но­го эха. Ес­ли спек­траль­ная ли­ния ре­зо­нанс­но­го кван­то­во­го пе­ре­хо­да в сре­де уши­ре­на су­ще­ст­вен­но не­од­но­род­но, т. е. $T_2^*≪T_2$, то по окон­ча­нии пер­во­го ре­зо­нанс­но­го им­пуль­са сво­бод­ная по­ля­ри­за­ция за­ту­ха­ет на­столь­ко бы­ст­ро, что энер­гия отд. из­лу­ча­те­лей за вре­мя поч­ти не из­ме­ня­ет­ся. То­гда, по­дав на сре­ду че­рез не­ко­то­рое вре­мя за­держ­ки $τ$ вто­рой ко­рот­кий ре­зо­нанс­ный им­пульс, мож­но из­ме­нить знак фа­зы ко­ле­ба­ний отд. ди­по­лей, а это при­во­дит к сме­не про­цес­са рас­фа­зи­ров­ки из­лу­ча­те­лей на про­цесс их фа­зи­ров­ки. В ре­зуль­та­те спус­тя оп­ре­де­лён­ное вре­мя мак­ро­ско­пич. по­ля­ри­за­ция вос­ста­нав­ли­ва­ет­ся, из­лу­чая све­то­вой им­пульс т. н. пер­вич­но­го (или двух­им­пульс­но­го) фо­тон­но­го эха. Варь­и­руя вре­мя за­держ­ки $τ$ , мож­но из­ме­рить вре­мя $T_2^*$ по умень­ше­нию ин­тен­сив­но­сти им­пуль­са эха. Ис­сле­до­ва­ние сиг­на­ла трёх­им­пульс­но­го (сти­му­ли­ро­ван­но­го) эха по­зво­ля­ет из­ме­рить вре­мя жиз­ни воз­бу­ж­дён­но­го уров­ня $T_1$. Изу­че­ние за­ви­си­мо­сти по­ля­ри­за­ции сиг­на­ла эха от по­ля­ри­за­ции воз­бу­ж­даю­щих им­пуль­сов да­ёт ин­фор­ма­цию о ти­пе на­блю­дае­мых кван­то­вых пе­ре­хо­дов.

Рис. 4. Схемы частотной (а) и временной (б) КАРС-спектроскопии комбинационных резонансов.

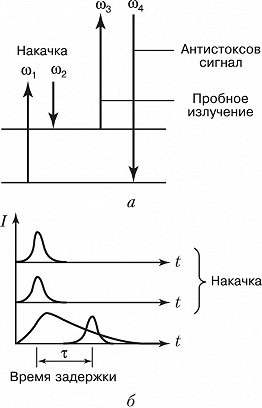
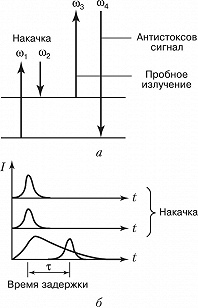
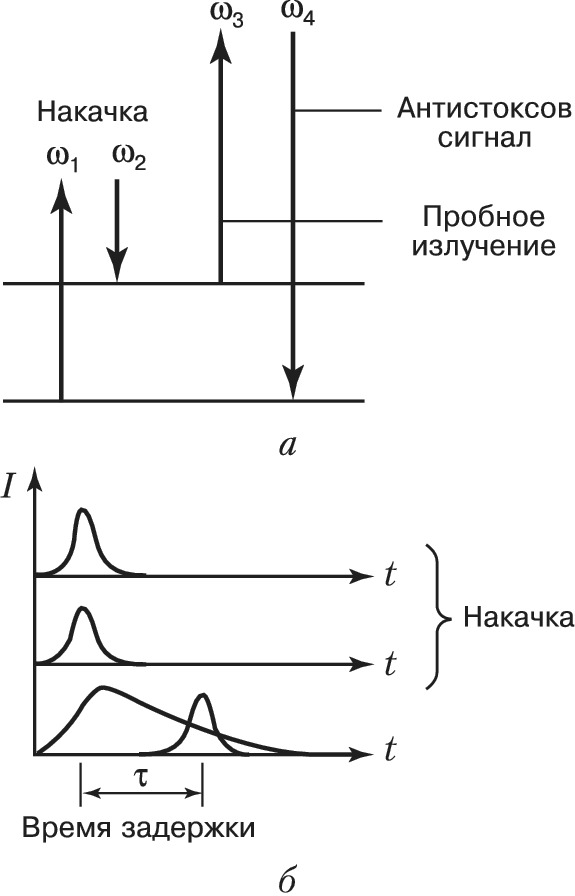
Эф­фек­ты, ана­ло­гич­ные за­ту­ха­нию сво­бод­ной по­ля­ри­за­ции, име­ют ме­сто и при мно­го­фо­тон­ном воз­бу­ж­де­нии кван­то­вых пе­ре­хо­дов, ко­гда оп­ре­де­лён­ная ком­би­на­ция час­тот па­даю­щих им­пуль­сов (напр., их сум­ма или раз­ность) сов­па­да­ет с час­то­той со­от­вет­ст­вую­ще­го кван­то­во­го пе­ре­хо­да. В этом слу­чае, од­на­ко, фор­ми­руе­мый мак­ро­ско­пич. от­клик сре­ды – ана­лог вол­ны по­ля­ри­за­ции при од­но­фо­тон­ном воз­бу­ж­де­нии – мо­жет ока­зать­ся не­из­лу­чаю­щим вслед­ст­вие пра­вил от­бо­ра (см. Мно­го­фо­тон­ные про­цес­сы, Мно­го­фо­тон­ное по­гло­ще­ние). Для его на­блю­де­ния ис­поль­зу­ют­ся до­пол­нит. (проб­ные) им­пуль­сы, в по­ле ко­то­рых ко­ге­рент­ный от­клик сре­ды во­вле­ка­ет­ся в про­цесс па­ра­мет­рич. сме­ше­ния час­тот (рис. 4, а). Ге­не­ри­руе­мое при этом из­лу­че­ние, как пра­ви­ло, от­ли­ча­ет­ся по час­то­те и по на­прав­ле­нию от воз­бу­ж­даю­ще­го. Ва­риа­ция вре­ме­ни за­держ­ки проб­но­го им­пуль­са $τ$ (рис. 4, б) от­но­си­тель­но воз­бу­ж­даю­щих им­пуль­сов да­ёт воз­мож­ность по умень­ше­нию ин­тен­сив­но­сти $I$ сиг­нала ко­ге­рент­но­го ан­ти­сто­ксо­ва рас­сея­ния (в на­прав­ле­нии син­хро­низ­ма) оп­ре­де­лить вре­мя ре­лак­са­ции $T_2$. Ес­ли же од­но­вре­мен­но из­ме­рять за­ту­ха­ние не­ко­ге­рент­но­го сиг­на­ла спон­тан­но­го ан­ти­сто­ксо­ва ком­би­на­ци­он­но­го рас­сея­ния, свя­зан­но­го с мно­го­фо­тон­ным за­се­ле­ни­ем верх­не­го уров­ня, то мож­но из­ме­рить вре­мя ре­лак­са­ции энер­гии $T_1$.

Ме­то­ды Н. с. весь­ма раз­но­об­раз­ны как по фи­зич. со­дер­жа­нию, так и по прак­тич. при­ло­же­ни­ям. С од­ной сто­ро­ны, бла­го­да­ря дос­ти­же­ни­ям Н. с. сверх­вы­со­ко­го раз­ре­ше­ния по­лу­че­ны ре­зуль­та­ты, важ­ней­шие для фун­дам. фи­зи­ки и мет­ро­ло­гии. С др. сто­ро­ны, не­ко­то­рые ме­то­ды, как, напр., КАРС-спек­тро­ско­пия, ста­ли ру­тин­ны­ми и во­шли в по­все­днев­ную прак­ти­ку не толь­ко мн. ис­сле­до­ва­тель­ских, но и про­из­водств. ла­бо­ра­то­рий.