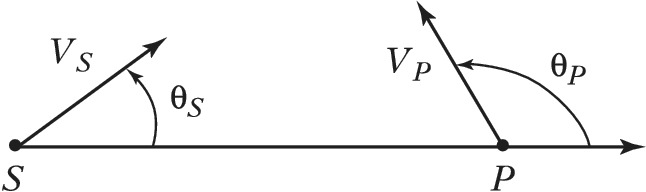ДО́ПЛЕРА ЭФФЕ́КТ

ДО́ПЛЕРА ЭФФЕ́КТ, из­ме­не­ние час­то­ты ко­ле­ба­ний $ω$ или дли­ны вол­ны $λ$, вос­при­ни­мае­мой на­блю­да­те­лем при дви­же­нии ис­точ­ни­ка ко­ле­ба­ний и на­блю­да­те­ля от­но­си­тель­но друг дру­га. Воз­ник­но­ве­ние Д. э. про­ще все­го объ­яс­нить на сле­дую­щем при­ме­ре. Пусть не­под­виж­ный ис­точ­ник в од­но­род­ной сре­де без дис­пер­сии ис­пус­ка­ет вол­ны с пе­рио­дом $T_0= λ_0/v$, где $λ_0$ – дли­на вол­ны, $v$ – фа­зо­вая ско­рость вол­ны в дан­ной сре­де. Не­под­виж­ный на­блю­да­тель бу­дет при­ни­мать из­лу­че­ние с та­ким же пе­рио­дом $Т_0$ и той же дли­ной вол­ны $λ_0$. Ес­ли же ис­точ­ник $S$ дви­жет­ся с не­ко­то­рой ско­ро­стью $V_S$ в сто­ро­ну на­блю­да­те­ля $P$ (при­ём­ни­ка), то дли­на при­ни­мае­мой на­блю­да­те­лем вол­ны умень­шит­ся на ве­ли­чи­ну сме­ще­ния ис­точ­ни­ка за пе­ри­од $T_0$, т. е. $λ=λ_0-V_ST_0$, а час­то­та $ω$ со­от­вет­ст­вен­но уве­ли­чит­ся: $ω=ω_0/(1-V_S/v)$. При­ни­мае­мая час­то­та уве­ли­чи­ва­ет­ся, ес­ли ис­точ­ник не­под­ви­жен, а на­блю­да­тель при­бли­жа­ет­ся к не­му. При уда­ле­нии ис­точ­ни­ка от на­блю­да­те­ля при­ни­мае­мая час­то­та умень­ша­ет­ся, что опи­сы­ва­ет­ся той же фор­му­лой, но с из­ме­нён­ным зна­ком ско­ро­сти.

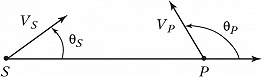
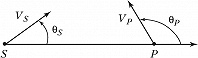
В об­щем слу­чае, ко­гда и ис­точ­ник, и при­ём­ник дви­жут­ся от­но­си­тель­но не­по­д­виж­ной сре­ды с не­ре­ля­ти­ви­ст­ски­ми ско­ро­стя­ми $V_S$ и $V_P$ под про­из­воль­ны­ми уг­ла­ми $θ_S$ и $θ_P$ (рис.), при­ни­мае­мая час­то­та рав­на:  $$\omega=\omega_0\frac{1-V_p\cos \theta_p/v}{1-V_s\cos \theta_p/v}.\tag1$$ Макс. уве­ли­че­ние час­то­ты про­ис­хо­дит при дви­же­нии ис­точ­ни­ка и при­ём­ни­ка на­встре­чу друг дру­гу $(θ_S=0, θ_P=π)$, а умень­ше­ние – при вза­им­ном уда­ле­нии ис­точ­ни­ка и на­блю­да­те­ля $(q_S=π, θ_P=0)$. Ес­ли же ис­точ­ник и при­ём­ник дви­жут­ся с оди­на­ко­вы­ми по ве­ли­чи­не и на­прав­ле­нию ско­ро­стя­ми, Д. э. от­сут­ст­ву­ет.

При ско­ро­стях дви­же­ния, срав­ни­мых со ско­ро­стью све­та $c$ в ва­куу­ме, не­об­хо­ди­мо при­нять во вни­ма­ние ре­ля­ти­ви­ст­ский эф­фект за­мед­ле­ния вре­ме­ни (см. От­но­си­тель­но­сти тео­рия

); в ре­зуль­та­те для не­под­виж­но­го на­блю­да­те­ля $(V_P=0)$ при­ни­мае­мая час­то­та из­лу­че­ния $$\omega=\omega_0\frac{\sqrt{1-\beta^2}}{1-(V_S/c)\cos \theta_S},\tag2$$ где $β=V_S/c$. В этом слу­чае сме­ще­ние час­то­ты име­ет ме­сто и при $θ_S=π/2$ (т. н. по­пе­реч­ный Д. э.). Для элек­тро­маг­нит­ных волн в ва­куу­ме в лю­бой сис­те­ме от­счё­та $v=c$ и в фор­му­ле (2) под $V_S$ нуж­но по­ни­мать от­но­сит. ско­рость ис­точ­ни­ка.

В сре­дах с дис­пер­си­ей, ко­гда фа­зо­вая ско­рость $v$ за­ви­сит от час­то­ты ω, со­от­но­ше­ния (1), (2) мо­гут до­пус­кать неск. зна­че­ний $ω$ для за­дан­ных $ω_0$ и $V_S$, т. е. в точ­ку на­блю­де­ния под од­ним и тем же уг­лом мо­гут при­хо­дить вол­ны с раз­ны­ми час­то­та­ми (т. н. слож­ный Д. э.). До­пол­нит. осо­бен­но­сти воз­ни­ка­ют при дви­же­нии ис­точ­ни­ка со ско­ро­стью $V_S>v$, ко­гда на по­верх­но­сти ко­ну­са уг­лов, удов­ле­тво­ряю­щих ус­ло­вию $\cosθ_S=v/V_S$, зна­ме­на­тель в фор­му­ле (2) об­ра­ща­ет­ся в нуль, – име­ет ме­сто т. н. ано­маль­ный Д. э. В этом слу­чае внут­ри ука­зан­но­го ко­ну­са час­то­та рас­тёт с уве­ли­че­ни­ем уг­ла $θ_S$, то­гда как при нор­маль­ном Д. э. под бóль­шими уг­ла­ми $θ_S$ из­лу­ча­ют­ся мень­шие час­то­ты.

Раз­но­вид­но­стью Д. э. яв­ля­ет­ся т. н. двой­ной Д. э. – сме­ще­ние час­то­ты волн при от­ра­же­нии их от дви­жу­щих­ся тел, по­сколь­ку от­ра­жаю­щий объ­ект мож­но рас­смат­ри­вать сна­ча­ла как при­ём­ник, а за­тем как пе­ре­из­лу­ча­тель волн. Ес­ли $ω_0$ и $v_0$ – час­то­та и фа­зо­вая ско­рость вол­ны, па­даю­щей на пло­скую гра­ни­цу, то час­то­ты $ω_i$ вто­рич­ных (от­ра­жён­ных и про­шед­ших) волн, рас­про­стра­няю­щих­ся со ско­ро­стя­ми $v_i$, оп­ре­де­ля­ют­ся как $$\omega_i=\omega_0\frac{1-(V/v_0)\cos \theta_0}{1-(V/v_i)\cos \theta_i},\tag3$$

Для не­ста­цио­нар­ных сред из­ме­не­ние час­то­ты рас­про­стра­няю­щих­ся волн мо­жет про­ис­хо­дить да­же для не­под­виж­ных из­лу­ча­те­ля и при­ём­ни­ка – т. н. па­ра­мет­ри­че­ский эф­фект До­п­ле­ра.

Д. э. на­зван в честь К. До­п­ле­ра

, ко­то­рый впер­вые тео­ре­ти­че­ски обос­но­вал его в аку­сти­ке и оп­ти­ке (1842). Пер­вое экс­пе­рим. под­твер­жде­ние Д. э. в аку­сти­ке от­но­сит­ся к 1845. А. Фи­зо

 >>

(1848) ввёл по­ня­тие до­п­ле­ров­ско­го сме­ще­ния спек­траль­ных ли­ний, ко­то­рое бы­ло об­на­ру­же­но позд­нее (1867) в спек­трах не­ко­то­рых звёзд и ту­ман­но­стей. По­пе­реч­ный Д. э. был об­на­ру­жен американскими фи­зи­ка­ми Г. Айв­сом и Д. Сти­лу­эл­лом в 1938. Об­об­ще­ние Д. э. на слу­чай не­ста­цио­нар­ных сред при­над­ле­жит В. А. Ми­хель­со­ну

 >>

(1899); на воз­мож­ность слож­но­го Д. э. в сре­дах с дис­пер­си­ей и ано­маль­но­го Д. э. при $V>v$ впер­вые ука­за­ли В. Л. Гинз­бург

 >>

и И. М. Франк

 >>

(1942).

Д. э. по­зво­ля­ет из­ме­рять ско­ро­сти дви­же­ния ис­точ­ни­ков из­лу­че­ния и рас­сеи­ваю­щих вол­ны объ­ек­тов и на­хо­дит ши­ро­кое прак­тич. при­ме­не­ние. В ас­т­ро­фи­зи­ке Д. э. ис­поль­зу­ет­ся для оп­ре­де­ле­ния ско­ро­сти дви­же­ния звёзд, а так­же ско­ро­сти вра­ще­ния не­бес­ных тел. Из­ме­ре­ния до­п­ле­ров­ско­го крас­но­го сме­ще­ния

ли­ний в спек­трах из­лу­че­ния уда­лён­ных га­лак­тик при­ве­ли к вы­во­ду о рас­ши­ряю­щей­ся Все­лен­ной. До­п­ле­ров­ское уши­ре­ние спек­траль­ных ли­ний

 >>

из­лу­че­ния ато­мов и ио­нов да­ёт спо­соб из­ме­ре­ния их темп-ры. В ра­дио- и гид­ро­ло­ка­ции Д. э. ис­поль­зу­ет­ся для из­ме­ре­ния ско­ро­сти дви­жу­щих­ся це­лей, для оп­ре­де­ле­ния их на фо­не не­под­виж­ных от­ра­жа­те­лей и т. п.