БИФУРКА́ЦИЯ

БИФУРКА́ЦИЯ (от би... и ср.-век. лат. furcatus – раз­дво­ен­ный, от лат. furca – дву­зу­бые ви­лы), раз­ветв­ле­ние, раз­двое­ние. В тео­рии ко­ле­ба­ний и тео­рии ди­на­ми­че­ских сис­тем Б. – это пе­ре­строй­ка ха­рак­те­ра дви­же­ния ре­аль­ной сис­те­мы (фи­зи­че­ской, хи­ми­че­ской, био­ло­ги­че­ской), пе­ре­ход её в но­вое ка­че­ст­вен­ное со­стоя­ние при ма­лом плав­ном из­ме­не­нии од­но­го или не­сколь­ких па­ра­мет­ров. Зна­че­ния па­ра­мет­ров, при ко­то­рых на­блю­да­ет­ся Б., на­зы­ва­ют­ся би­фур­ка­ци­он­ны­ми. Ма­те­ма­ти­че­ски Б. – это из­ме­не­ние струк­ту­ры раз­бие­ния фа­зо­во­го про­стран­ст­ва ди­на­мич. сис­те­мы на тра­ек­то­рии при ма­лом из­ме­не­нии её па­ра­мет­ров.

Тео­рия Б. да­ёт воз­мож­ность по­нять как фи­зич. яв­ле­ния в ме­ха­ни­ке (по­ве­де­ние час­ти­цы в по­тен­ци­аль­ной яме), оп­ти­ке (ус­ло­вие воз­ник­но­ве­ния ла­зер­ной ге­не­ра­ции), тео­рии ко­ле­ба­ний (ав­то­ко­ле­ба­ния), так и не­ко­то­рые хи­мич. про­цес­сы (напр., ко­ле­ба­тель­ные ре­ак­ции ти­па ре­ак­ции Бе­ло­усо­ва – Жа­бо­тин­ско­го). Кро­ме то­го, тео­рия Б. при­ме­ни­ма для опи­са­ния ря­да яв­ле­ний в эко­ло­гии и ди­на­ми­ке по­пу­ля­ций, ус­ло­вий со­су­ще­ст­во­ва­ния ви­дов (хищ­ник – жерт­ва), про­цес­сов эво­лю­ции и му­та­ций в био­ло­гии, взаи­мо­дей­ст­вия и раз­ви­тия со­ци­аль­ных сис­тем и др.

Рис. 1.

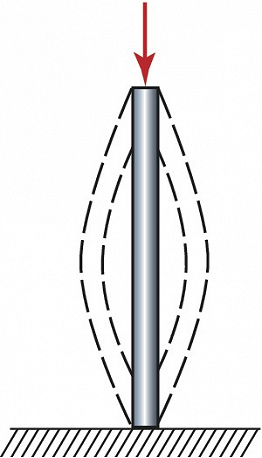
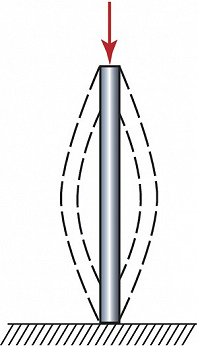
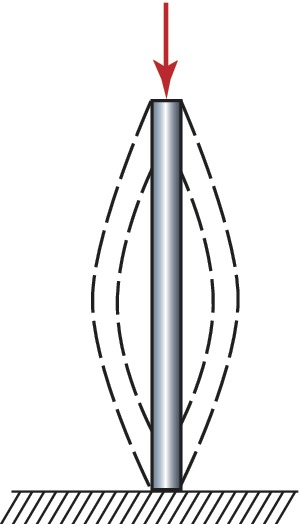
Про­стей­шим при­ме­ром Б. яв­ля­ет­ся рас­смот­рен­ное Л. Эй­ле­ром вы­пу­чи­ва­ние в ту или иную сто­ро­ну вер­ти­каль­но на­гру­жен­но­го стерж­ня при пре­вы­ше­нии кри­тической на­груз­ки (рис. 1). Тео­рия Б. уни­вер­саль­на. Зна­ние основных ти­пов Б. по­зво­ля­ет су­ще­ст­вен­но об­лег­чить ис­сле­до­ва­ние ре­аль­ных сис­тем, пред­ска­зать ха­рак­тер но­вых дви­жений, воз­ни­каю­щих в мо­мент пе­ре­хо­да сис­те­мы в ка­че­ст­вен­но дру­гое со­стоя­ние, оце­нить их ус­той­чи­вость и об­ласть су­ще­ст­во­ва­ния.

Ос­но­вы тео­рии Б. за­ло­же­ны А. Пу­ан­ка­ре и А. М. Ля­пу­но­вым в нач. 20 в. Важ­ней­ший вклад в её раз­ви­тие сде­лан А. А. Ан­д­ро­но­вым и Л. С. Пон­тря­ги­ным, ко­то­рые вве­ли по­ня­тие гру­бо­сти (струк­тур­ной ус­той­чи­во­сти) ди­на­мич. сис­тем на плос­ко­сти. Гру­бые сис­те­мы со­хра­ня­ют ка­че­ст­вен­ную струк­ту­ру раз­бие­ния фа­зо­во­го про­стран­ст­ва на тра­ек­то­рии при ма­лых из­ме­не­ни­ях па­ра­мет­ров. На­ру­ше­ние ус­ло­вий гру­бо­сти про­ис­хо­дит при би­фур­ка­ци­он­ных зна­че­ни­ях па­ра­мет­ров, ко­гда сис­те­ма ста­но­вит­ся не­гру­бой. Наи­бо­лее рас­про­стра­нён­ны­ми ти­па­ми по­ве­де­ния сис­тем разл. про­ис­хо­ж­де­ния яв­ля­ют­ся со­стоя­ния рав­но­ве­сия и пе­рио­дич. дви­же­ния. Ма­те­ма­тич. об­ра­зом пе­рио­дич. дви­же­ния яв­ля­ет­ся пре­дель­ный цикл. Тео­рия Б. для сис­тем, об­ла­даю­щих со­стоя­ния­ми рав­но­ве­сия и пре­дель­ны­ми цик­ла­ми, раз­ра­бо­та­на в осн. А. А. Ан­д­ро­но­вым и его уче­ни­ка­ми.

Рис. 2.

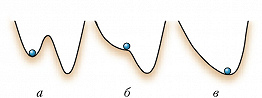
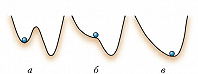
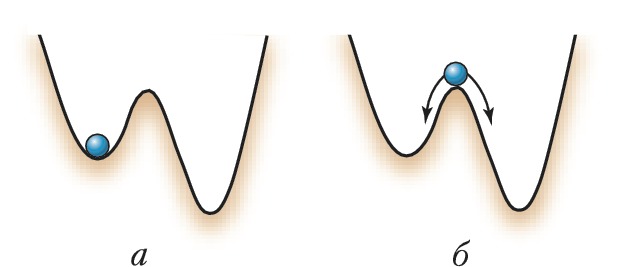
Сис­те­ма на­хо­дит­ся в ус­той­чи­вом со­стоя­нии (со­стоя­нии ус­той­чи­во­го рав­но­ве­сия), ес­ли при ма­лом от­кло­не­нии от не­го она воз­вра­ща­ет­ся вновь к это­му со­стоя­нию (рис. 2а). В этом смыс­ле та­кие по­ло­же­ния рав­но­ве­сия слов­но при­тя­ги­ва­ют к се­бе, по­это­му они на­зы­ва­ют­ся ат­трак­то­ра­ми (от англ. attract – при­тя­ги­вать). Ка­ж­дый ат­трак­тор име­ет свою об­ласть при­тя­же­ния – мно­же­ст­во на­чаль­ных ус­ло­вий (ко­ор­ди­нат и ско­ро­стей ша­ри­ка, как на рис. 2а), при от­кло­не­нии от ко­то­рых сис­те­ма с те­че­ни­ем вре­ме­ни воз­вра­ща­ет­ся в это же со­стоя­ние. Сис­те­ма на­хо­дит­ся в со­стоя­нии не­ус­той­чи­во­го рав­но­ве­сия, ес­ли при ма­лом от­кло­не­нии от не­го она не воз­вра­ща­ет­ся в это со­стоя­ние (рис. 2б).

Рис. 3.

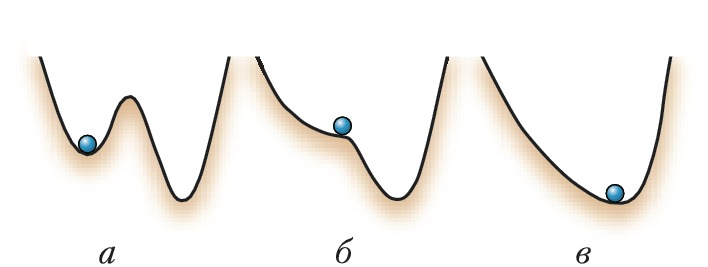
Сис­те­ма, на­хо­дя­щая­ся в ус­той­чи­вом ста­цио­нар­ном со­стоя­нии, мо­жет ис­пы­ты­вать Б., ко­гда оно те­ря­ет ус­той­чи­вость, напр. сли­ва­ет­ся с не­ус­той­чи­вым (рис. 3а–в). В этом слу­чае с пе­ре­хо­дом па­ра­мет­ра че­рез би­фур­ка­ци­он­ное зна­че­ние (рис. 3б) сис­те­ма скач­ком пе­ре­хо­дит в др. об­ласть, уда­лён­ную от ис­ход­ной (рис. 3в).

Б., при ко­то­рой со­стоя­ние ус­той­чи­во­го рав­но­ве­сия сис­те­мы, на­блю­дае­мое до пе­ре­хо­да па­ра­мет­ра че­рез точ­ку Б., сме­ня­ет­ся ус­той­чи­вым пе­рио­дич. дви­же­ни­ем, бы­ла ис­сле­до­ва­на А. А. Анд­ро­но­вым и Э. Хоп­фом и но­сит их имя. Дру­гой тип Б. Анд­ро­но­ва – Хоп­фа – это жё­ст­кое воз­бу­ж­де­ние, ко­гда па­ра­метр сис­те­мы из­ме­ня­ет­ся так, что не­ус­той­чи­вый пре­дель­ный цикл стя­ги­ва­ет­ся к ста­цио­нар­но­му ус­той­чи­во­му со­стоя­нию и в мо­мент Б. сли­ва­ет­ся с ним. При этом об­ласть при­тя­же­ния ста­цио­нар­но­го со­стоя­ния сис­те­мы и раз­ме­ры пре­дель­но­го цик­ла умень­ша­ют­ся до ну­ля, так что сис­те­ма те­ря­ет ус­той­чи­вость и скач­ком пе­ре­хо­дит на др. ре­жим дви­же­ния.

Ус­той­чи­вое пе­рио­дич. дви­же­ние так­же мо­жет пре­тер­петь Б., ли­бо слив­шись с не­ус­той­чи­вым пе­рио­дич. дви­же­ни­ем, ли­бо по­те­ряв свою ус­той­чи­вость. В по­след­нем слу­чае из пе­рио­дич. дви­же­ний мо­гут воз­ник­нуть пе­рио­дич. дви­же­ния уд­во­ен­но­го пе­рио­да или ква­зи­пе­рио­дич. ко­ле­ба­ния (т. н. дву­мер­ный ин­ва­ри­ант­ный тор). Ква­зи­пе­рио­дич. ко­ле­ба­ния – это дви­же­ния с дву­мя или бо­лее не­со­изме­ри­мы­ми (ра­цио­наль­но не­за­ви­си­мы­ми) час­то­та­ми. Та­кие ко­ле­ба­ния на­блю­да­ют­ся, напр., в сис­те­ме двух свя­зан­ных ма­ят­ни­ков с час­то­та­ми $ω_1$ и $ω_2$ при $ω_1/ω_2≠k/m$, где $k$ и $m$ – це­лые чис­ла.

В не­ли­ней­ных сис­те­мах при из­ме­не­нии па­ра­мет­ров до­пус­ти­ма ко­неч­ная (или да­же бес­ко­неч­ная) по­сле­до­ва­тель­ность Б., при­во­дя­щая к по­яв­ле­нию ди­на­ми­че­ско­го хао­са (см. так­же Стран­ный ат­трак­тор).