ПРЕДЕ́ЛЬНЫЙ ЦИКЛ

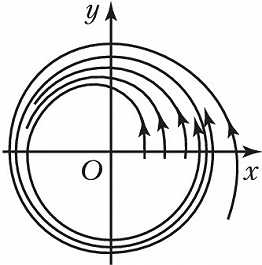
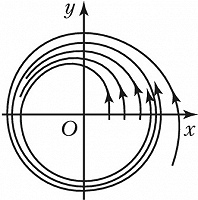
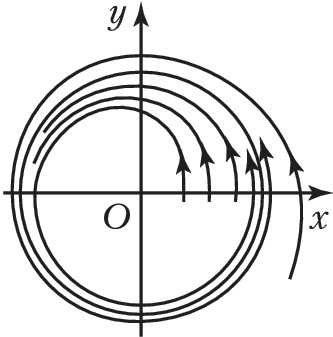
ПРЕДЕ́ЛЬНЫЙ ЦИКЛ сис­те­мы диф­фе­рен­ци­аль­ных урав­не­ний 2-го по­ряд­ка $$\frac{dx}{dt}=P(x,y),\,\,\frac{dy}{dt}=Q(x,y),$$ замк­ну­тая тра­ек­то­рия в фа­зо­вом про­стран­ст­ве $Oxy$, об­ла­даю­щая тем свой­ст­вом, что все тра­ек­то­рии, на­чи­наю­щие­ся в дос­та­точ­но уз­кой коль­це­об­раз­ной её ок­ре­ст­но­сти, не­ог­ра­ни­чен­но при­бли­жа­ют­ся к этой тра­ек­то­рии при $t→+∞$ (ус­той­чи­вый П. ц.), или при $t→–∞$ (не­ус­той­чи­вый П. ц.), или часть из них при $t→+∞$, а ос­таль­ные – при $t→–∞$ (по­лу­ус­той­чи­вый П. ц.). Напр., сис­те­ма $$\frac{dr}{dt}=1-r,\quad \frac{dφ}{dt}=1$$ ($r$ и $φ$ – по­ляр­ные ко­ор­ди­на­ты), об­щее ре­ше­ние ко­то­рой $r=1-(1-r_0)e^{-t}$, $φ=φ_0+t$, где $r_0⩾0$, име­ет ус­той­чи­вый П. ц. $r=1$ (рис.). По­ня­тие «П. ц.» пе­рено­сит­ся и на сис­те­мы $n$-го по­ряд­ка. С точ­ки зре­ния ме­ха­ни­ки ус­той­чи­вый П. ц. со­от­вет­ст­ву­ет ус­той­чи­во­му пе­рио­дич. дви­же­нию сис­те­мы. По­это­му по­иск П. ц. име­ет важ­ное зна­че­ние в тео­рии не­ли­ней­ных ко­ле­ба­ний.