КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ

КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, со­во­куп­ность яв­ле­ний, обу­слов­лен­ных по­верх­но­ст­ным на­тя­же­ни­ем

на гра­ни­це раз­де­ла не­сме­ши­ваю­щих­ся сред (в сис­те­мах жид­кость – жид­кость, жид­кость – газ или пар) при на­ли­чии ис­крив­ле­ния по­верх­но­сти. Ча­ст­ный слу­чай по­верх­но­ст­ных яв­ле­ний

 >>

.

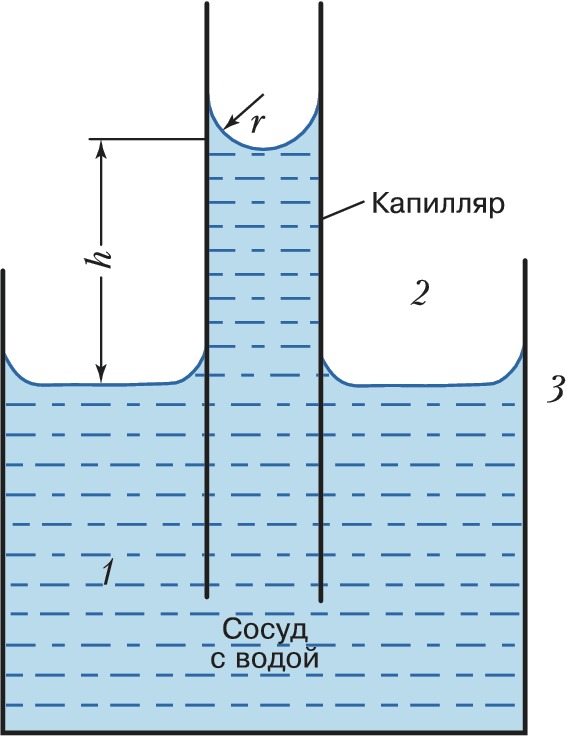
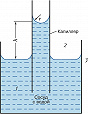
При от­сут­ст­вии си­лы тя­же­сти жид­кость ог­ра­ни­чен­ной мас­сы под воз­дей­ст­ви­ем по­верх­но­ст­но­го на­тя­же­ния стре­мит­ся за­нять объ­ём с ми­ним. по­верх­но­стью, т. е. при­ни­ма­ет фор­му ша­ра. В ус­ло­ви­ях дей­ст­вия си­лы тя­же­сти не слиш­ком вяз­кая жид­кость дос­та­точ­ной мас­сы при­ни­ма­ет фор­му со­су­да, в ко­то­рый на­ли­та, и её сво­бод­ная по­верх­ность при от­но­си­тель­но боль­шой пло­ща­ди (вда­ли от сте­нок со­су­да) ста­но­вит­ся пло­ской, т. к. роль по­верх­но­ст­но­го на­тя­же­ния ме­нее су­ще­ст­вен­на, чем си­лы тя­же­сти. При взаи­мо­дей­ст­вии с по­верх­но­стью др. жид­ко­сти или твёр­до­го те­ла (напр., со стен­ка­ми со­су­да) по­верх­ность рас­смат­ри­вае­мой жид­ко­сти ис­крив­ля­ет­ся в за­ви­си­мо­сти от на­ли­чия или от­сут­ст­вия сма­чи­ва­ния

. Ес­ли име­ет ме­сто сма­чи­ва­ние, т. е. мо­ле­ку­лы жид­ко­сти 1 (рис. 1) силь­нее взаи­мо­дей­ст­ву­ют с мо­ле­ку­ла­ми по­верх­но­сти 3, чем с мо­ле­ку­ла­ми др. жид­ко­сти (или га­за) 2, то под воз­дей­ст­ви­ем раз­но­сти сил меж­мо­ле­ку­ляр­но­го взаи­мо­дей­ст­вия жид­кость 1 под­ни­ма­ет­ся по стен­ке со­су­да – уча­сток жид­ко­сти, при­мы­каю­щий к стен­ке, ис­крив­ля­ет­ся. Дав­ле­ние, вы­зы­вае­мое подъ­ё­мом жид­ко­сти, урав­но­ве­ши­ва­ет­ся ка­пил­ляр­ным дав­ле­ни­ем $\Delta p$ – раз­но­стью дав­ле­ний над и под ис­крив­лён­ной по­верх­но­стью раз­де­ла. Ве­ли­чи­на ка­пил­ляр­но­го дав­ле­ния за­ви­сит от сред­не­го ра­диу­са $r$ кри­виз­ны по­верх­но­сти и оп­ре­де­ля­ет­ся фор­му­лой Ла­п­ла­са: $\Delta p=2 \sigma/r$, где $\sigma$  – по­верх­но­ст­ное на­тя­же­ние. Ес­ли гра­ни­ца раз­де­ла фаз пло­ская ($r= \infty$), то в ус­ло­ви­ях ме­ха­нич. рав­но­ве­сия сис­те­мы дав­ле­ния с обе­их сто­рон гра­ни­цы раз­де­ла рав­ны и $\Delta p=0$. В слу­чае во­гну­той по­верх­но­сти жид­ко­сти ($r \lt 0$) дав­ле­ние в жид­ко­сти ни­же, чем дав­ле­ние в гра­ни­ча­щей с ней фа­зе и $\Delta p \lt 0$; для вы­пук­лой по­верх­но­сти ($r>0$) $\Delta p>0$.

Ес­ли стен­ки со­су­да при­бли­зить друг к дру­гу, зо­ны ис­крив­ле­ния по­верх­но­сти жид­ко­сти об­ра­зу­ют ме­ниск – пол­но­стью ис­крив­лён­ную по­верх­ность. Об­ра­зо­вав­шая­ся сис­те­ма на­зы­ва­ет­ся ка­пил­ля­ром; в нём в ус­ло­ви­ях сма­чи­ва­ния дав­ле­ние под ме­ни­ском по­ни­же­но и жид­кость в ка­пил­ля­ре под­ни­ма­ет­ся (над уров­нем сво­бод­ной по­верх­но­сти жид­ко­сти в со­су­де); вес стол­ба жид­ко­сти вы­со­той $h$ урав­но­ве­ши­ва­ет ка­пил­ляр­ное дав­ле­ние $\Delta p$. Не­сма­чи­ваю­щая жид­кость в ка­пил­ля­ре об­ра­зу­ет вы­пук­лый ме­ниск, дав­ле­ние над ко­то­рым вы­ше, и жид­кость в нём опус­ка­ет­ся ни­же уров­ня сво­бод­ной по­верх­но­сти вне ка­пил­ля­ра. Вы­со­та под­ня­тия (опус­ка­ния) жид­ко­сти в ка­пил­ля­ре от­но­си­тель­но сво­бод­ной по­верх­но­сти (где $r= \infty$ и $\Delta p=0$) оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем: $h=2 \sigma \cos \theta/ \Delta \rho gr$, где $\theta$  – крае­вой угол (угол ме­ж­ду ка­са­тель­ной к по­верх­но­сти ме­ни­ска и стен­кой ка­пил­ля­ра), $\Delta \rho$ – раз­ность плот­но­стей жид­ко­сти 1 в ка­пил­ля­ре и внеш­ней сре­ды 2, $g$ – ус­ко­ре­ние сво­бод­но­го па­де­ния.

Ис­крив­ле­ние по­верх­но­сти влия­ет на ус­ло­вия рав­но­ве­сия ме­ж­ду жид­ко­стью и её на­сы­щен­ным па­ром: со­глас­но Кель­ви­на урав­не­нию

, дав­ле­ние па­ров над ка­п­лей жид­ко­сти по­вы­ша­ет­ся с умень­ше­ни­ем её ра­диу­са, что объ­яс­ня­ет, напр., рост боль­ших ка­пель в об­ла­ках за счёт ма­лых.

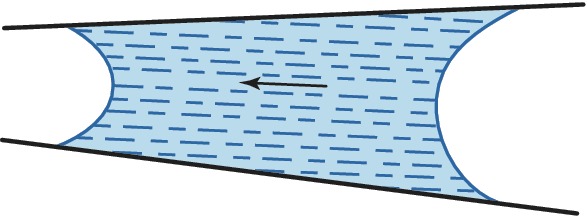
К ха­рак­тер­ным К. я. от­но­сят­ся ка­пил­ляр­ное впи­ты­ва­ние, по­яв­ле­ние и рас­про­стра­не­ние ка­пил­ляр­ных волн

, ка­пил­ляр­ное пе­ре­дви­же­ние жид­ко­сти, ка­пил­ляр­ная кон­ден­са­ция, про­цес­сы ис­па­ре­ния и рас­тво­ре­ния при на­ли­чии ис­крив­лён­ной по­верх­но­сти. Ка­пил­ляр­ное впи­ты­ва­ние ха­рак­те­ри­зу­ет­ся ско­ро­стью, за­ви­ся­щей от ка­пил­ляр­но­го дав­ле­ния и вяз­ко­сти жид­ко­сти. Оно иг­ра­ет су­ще­ст­вен­ную роль в во­до­снаб­же­нии рас­те­ний, дви­же­нии во­ды в поч­вах и др. про­цес­сах, свя­зан­ных с дви­же­ни­ем жид­ко­стей в по­рис­тых сре­дах. Ка­пил­ляр­ная про­пит­ка – один из рас­про­стра­нён­ных про­цес­сов хи­мич. тех­но­ло­гии. В сис­те­мах с не­па­рал­лель­ны­ми стен­ка­ми (или ка­пил­ля­рах ко­нич. се­че­ния) кри­виз­на ме­ни­сков за­ви­сит от рас­по­ло­же­ния в них гра­нич­ных по­верх­но­стей жид­ко­сти, и ка­п­ля сма­чи­ваю­щей жид­ко­сти в них на­чи­на­ет дви­гать­ся к ме­ни­ску с мень­шим ра­диу­сом (рис. 2), т. е. в ту сто­ро­ну, где дав­ле­ние ни­же. При­чи­ной ка­пил­ляр­но­го пе­ре­дви­же­ния жид­ко­сти мо­жет слу­жить и раз­ни­ца сил по­верх­но­ст­но­го на­тя­же­ния в ме­ни­сках, напр. при су­ще­ст­во­ва­нии гра­ди­ен­та темп-ры или при ад­сорб­ции по­верх­но­ст­но-ак­тив­ных ве­ществ

 >>

, сни­жаю­щих по­верх­но­ст­ное на­тя­же­ние.

Ка­пил­ляр­ной кон­ден­са­ци­ей на­зы­ва­ют про­цесс кон­ден­са­ции па­ра в ка­пил­ля­рах и мик­ро­тре­щи­нах по­рис­тых тел, а так­же в про­ме­жут­ках ме­ж­ду сбли­жен­ны­ми твёр­ды­ми час­ти­ца­ми или те­ла­ми. Не­об­хо­ди­мое ус­ло­вие ка­пил­ляр­ной кон­ден­са­ции – на­ли­чие сма­чи­ва­ния по­верх­но­сти тел (час­тиц) кон­ден­си­рую­щей­ся жид­ко­стью. Про­цес­су ка­пил­ляр­ной кон­ден­са­ции пред­ше­ст­ву­ет ад­сорб­ция мо­ле­кул па­ра по­верх­но­стью тел и об­ра­зо­ва­ние ме­ни­сков жид­ко­сти. В ус­ло­ви­ях сма­чи­ва­ния фор­ма ме­ни­сков во­гну­тая и дав­ле­ние $p$ на­сы­щен­но­го па­ра над ни­ми ни­же, чем дав­ле­ние на­сы­щен­но­го па­ра $p_0$ при тех же ус­ло­ви­ях над пло­ской по­верх­но­стью. Т. е. ка­пил­ляр­ная кон­ден­са­ция про­ис­хо­дит при бо­лее низ­ких, чем $p_0$, дав­ле­ни­ях.

Ис­крив­ле­ние по­верх­но­сти жид­ко­сти мо­жет су­ще­ст­вен­но вли­ять на про­цес­сы ис­па­ре­ния, ки­пе­ния, рас­тво­ре­ния, за­ро­ды­ше­об­ра­зо­ва­ния при кон­ден­са­ции па­ра и кри­стал­ли­за­ции. Так, свой­ст­ва сис­тем, со­дер­жа­щих боль­шое ко­ли­че­ст­во ка­пель или пу­зырь­ков га­за (эмуль­сий, аэ­ро­зо­лей, пен), и их фор­ми­ро­ва­ние во мно­гом оп­ре­де­ля­ют­ся К. я. Они ле­жат так­же в ос­но­ве мн. тех­но­ло­гич. про­цес­сов: фло­та­ции, спе­ка­ния по­рош­ков, вы­тес­не­ния неф­ти из пла­стов вод­ны­ми рас­тво­ра­ми по­верх­но­ст­но-ак­тив­ных ве­ществ, ад­сорб­ци­он­но­го раз­де­ле­ния и очи­ст­ки га­зо­вых и жид­ких сме­сей и т. п.

Впер­вые К. я. бы­ли ис­сле­до­ва­ны Ле­о­нар­до да Вин­чи. Сис­те­ма­тич. на­блю­де­ния и опи­са­ния К. я. в тон­ких труб­ках и ме­ж­ду пло­ски­ми, близ­ко рас­по­ло­жен­ны­ми стек­лян­ны­ми пла­сти­на­ми про­вёл в 1709 Ф. Хокс­би, де­мон­ст­ра­тор Лон­дон­ско­го ко­ро­лев­ско­го об-ва. Ос­но­вы тео­рии К. я. за­ло­же­ны в тру­дах Т. Юн­га

, П. Ла­п­ла­са

 >>

, а их тер­мо­ди­на­мич. рас­смот­ре­ние осу­ще­ст­вил Дж. Гиббс

 >>

(1876).