КОШИ́ РАСПРЕДЕЛЕ́НИЕ

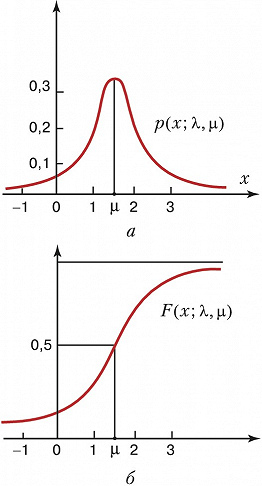
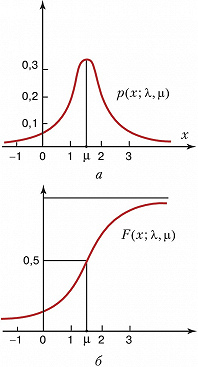
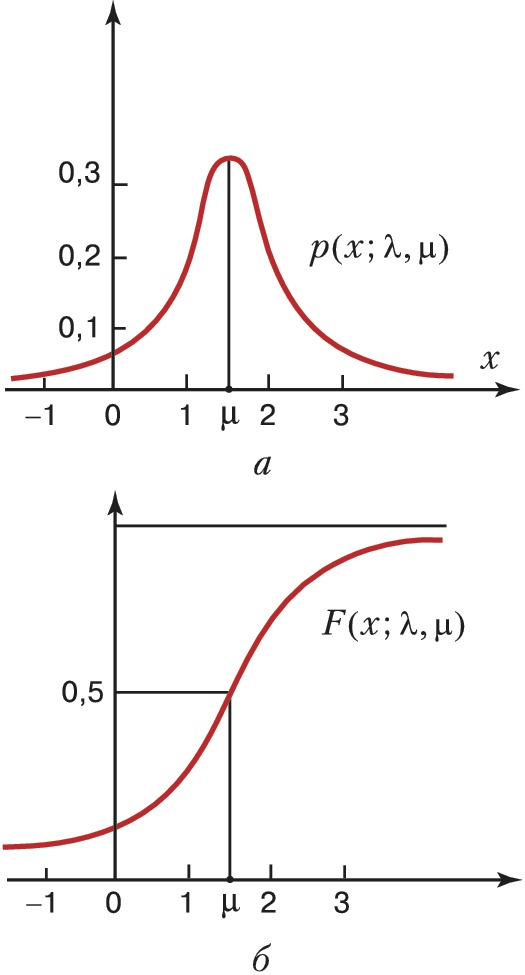
КОШИ́ РАСПРЕДЕЛЕ́НИЕ, рас­пре­де­ле­ние ве­ро­ят­но­стей слу­чай­ной ве­ли­чи­ны $X$, имею­щее плот­ность $$p(x; \lambda, \mu)={1 \over\pi}\frac{\lambda}{\pi\lambda^2+(x-\mu)^2},\,-∞<х<∞,$$ где $-∞<μ<∞$ и $λ>0$ – па­ра­мет­ры. К. р. уни­мо­даль­но и сим­мет­рич­но от­но­си­тель­но точ­ки $x=μ$, яв­ляю­щей­ся мо­дой и ме­диа­ной это­го рас­пре­де­ле­ния [на рис. а и б изображены графики плот­но­сти $p(x; λ, μ)$ и соответствующей функции распределения $F(x; λ, μ)$ при $μ=1,5$ и $λ=1$]. Ма­те­ма­ти­че­ское ожи­да­ние К. р. не су­ще­ст­ву­ет. Ха­рак­те­ри­сти­че­ская функ­ция К. р. рав­на $e^{iμt-λ|t|},\,-\infty \lt t \lt \infty$. Про­из­воль­ное К. р. с па­ра­мет­ра­ми $μ$ и $λ$ вы­ра­жа­ет­ся че­рез стан­дарт­ное К. р. с па­ра­мет­ра­ми 0 и 1 фор­му­лой $$p(x;\mu,\lambda)={1 \over\lambda}p\left(\frac{x-\mu}{\lambda}\right),$$ где $$p(x)=\frac{1}{\pi(1+x^2)}.$$

Ес­ли не­за­ви­си­мые слу­чай­ные ве­ли­чи­ны $X_1,\ldots,X_n$ име­ют од­но и то же К. р., то их ариф­ме­тич. сред­нее $(X_1+ ...+X_n)/n$ для лю­бо­го $n=1,2,...$ име­ет то же са­мое рас­пре­де­ле­ние; этот факт был ус­та­нов­лен С. Пу­ас­со­ном (1830). К. р. яв­ля­ет­ся ус­той­чи­вым рас­пре­де­ле­ни­ем. От­но­ше­ние $X/Y$ не­за­ви­си­мых слу­чай­ных ве­ли­чин $X$ и $Y$ со стан­дарт­ным нор­маль­ным рас­пре­де­ле­ни­ем име­ет К. р. с па­ра­мет­ра­ми 0 и 1. Рас­пре­де­ле­ние тан­ген­са $\text{tg} Z$ слу­чай­ной ве­ли­чи­ны $Z$, с рав­но­мер­ным рас­пре­де­ле­ни­ем на от­рез­ке $[-π/2, π/2]$, так­же име­ет К. р. с па­ра­мет­ра­ми 0 и 1. К. р. рас­смат­ри­ва­лось О. Ко­ши (1853).