КАРТОГРАФИ́ЧЕСКИЕ ПРОЕ́КЦИИ
-
Рубрика: География
-
-
Скопировать библиографическую ссылку:
КАРТОГРАФИ́ЧЕСКИЕ ПРОЕ́КЦИИ, математич. способы отображения всей поверхности земного эллипсоида или его части на плоскости карты. К. п. устанавливают соответствие между геодезич. координатами точек (широтой $B$ и долготой $L$) и их прямоугольными координатами ($X$ и $Y$) на карте: $$X=f_1(B,L); Y=f_2(B,L).$$Конкретные реализации функций $f_1$ и $f_2$ часто сложны, их число бесконечно, и, следовательно, разнообразие К. п. неограниченно. Исходная аксиома К. п. состоит в том, что сферич. поверхность нельзя развернуть на плоскость без деформаций – сжатий и растяжений, различных по величине и направлению. Математич. картография изучает все виды искажений и разрабатывает методы построения проекций, в которых искажения имели бы или наименьшие (в к.-л. смысле) значения, или заранее заданное распределение. Разные К. п. могут иметь следующие виды искажений: искажения длин – масштаб длин и расстояний непостоянен в разных точках карты и по разным направлениям; искажения площадей – масштаб площадей в разных точках карты различен, что нарушает размеры объектов; искажения углов – углы между направлениями на карте искажены относительно углов на местности; искажения форм – фигуры на карте деформированы и не подобны фигурам на местности, что является следствием искажения углов.
В любой К. п. различают главный масштаб длин и площадей – отношение, показывающее степень уменьшения размеров эллипсоида (шара) относительно его изображения на карте, и частные масштабы – отношение бесконечно малого отрезка (или площади), изображённого на карте, к соответствующей бесконечно малой величине на эллипсоиде (шаре). Картографические анимации имеют ещё и временной масштаб, т. е. отношение времени демонстрации карты к реальному времени изображаемого процесса.
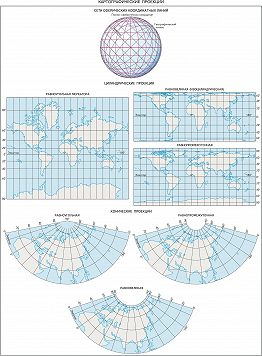
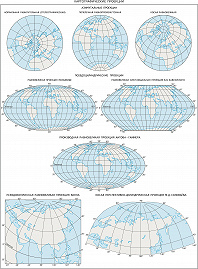
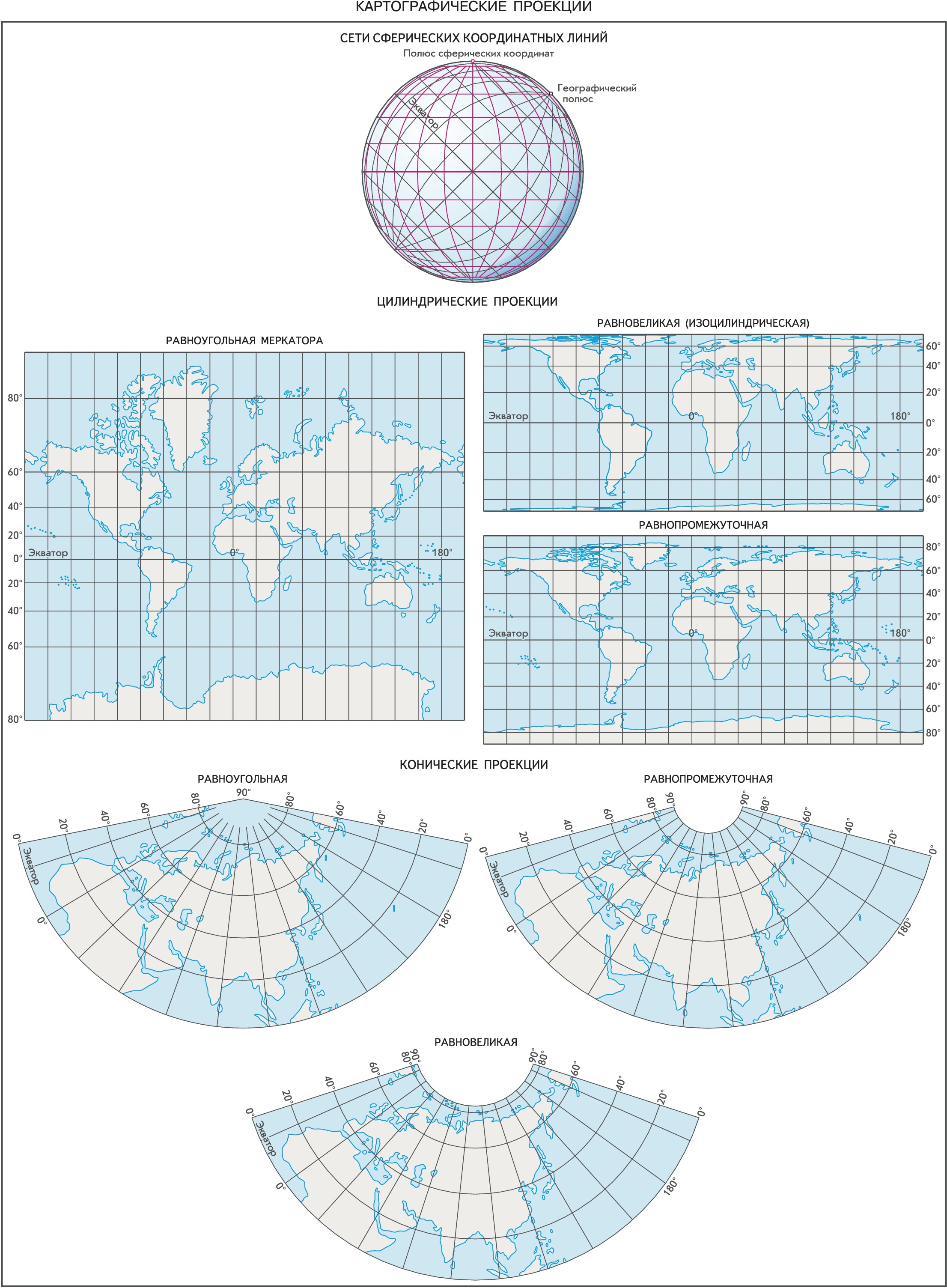
По характеру искажений, возникающих при переходе от сферич. поверхности к плоскости, К. п. подразделяют на равновеликие, которые сохраняют размеры площадей, равноугольные, оставляющие без искажений углы и формы контуров (ранее их называли конформными), и произвольные, где площади и углы искажены в разных соотношениях. Частный случай произвольных К. п. – равнопромежуточные проекции, в которых масштаб постоянен по одному из гл. направлений (по меридиану или параллели). См. карты Картографические проекции.
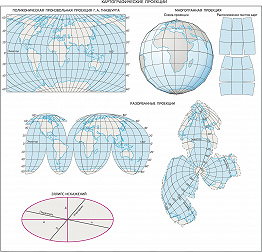
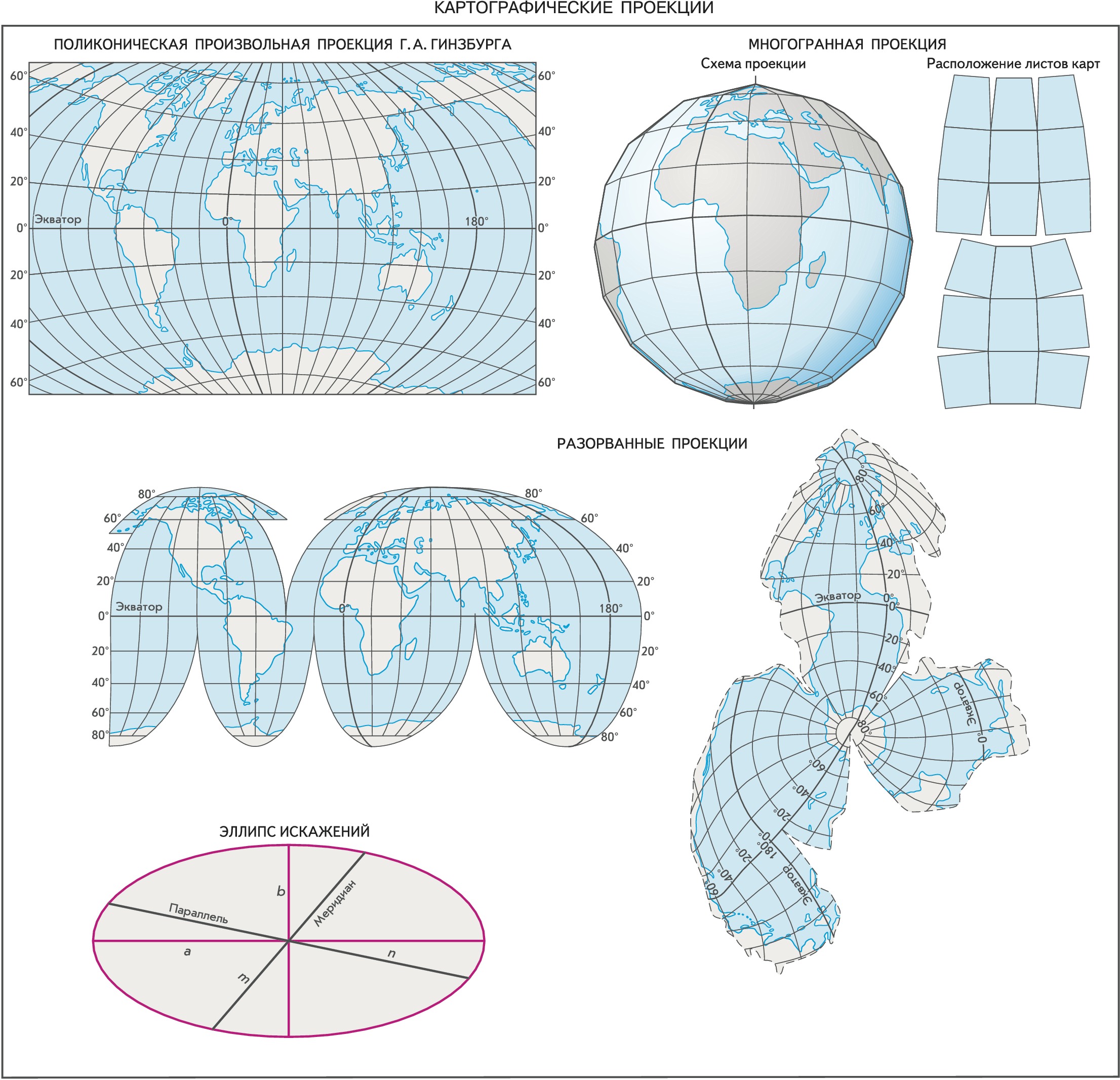
Мерой деформаций в К. п. служит эллипс искажений (или индикатриса Тиссо). Любая бесконечно малая окружность на земном шаре (эллипсоиде) предстаёт на карте бесконечно малым эллипсом, размеры и форма которого отражают искажения длин, площадей и углов. Длина и ориентировка большой оси эллипса искажений соответствуют направлению наибольшего растяжения (a) в данной точке, а малая ось – наибольшего сжатия (b), отрезки вдоль меридиана и параллели характеризуют частные масштабы вдоль них (m и n).
Искажения на картах можно также показывать с помощью особых изолиний – изокол, т. е. линий равных искажений длин, площадей, углов или форм.
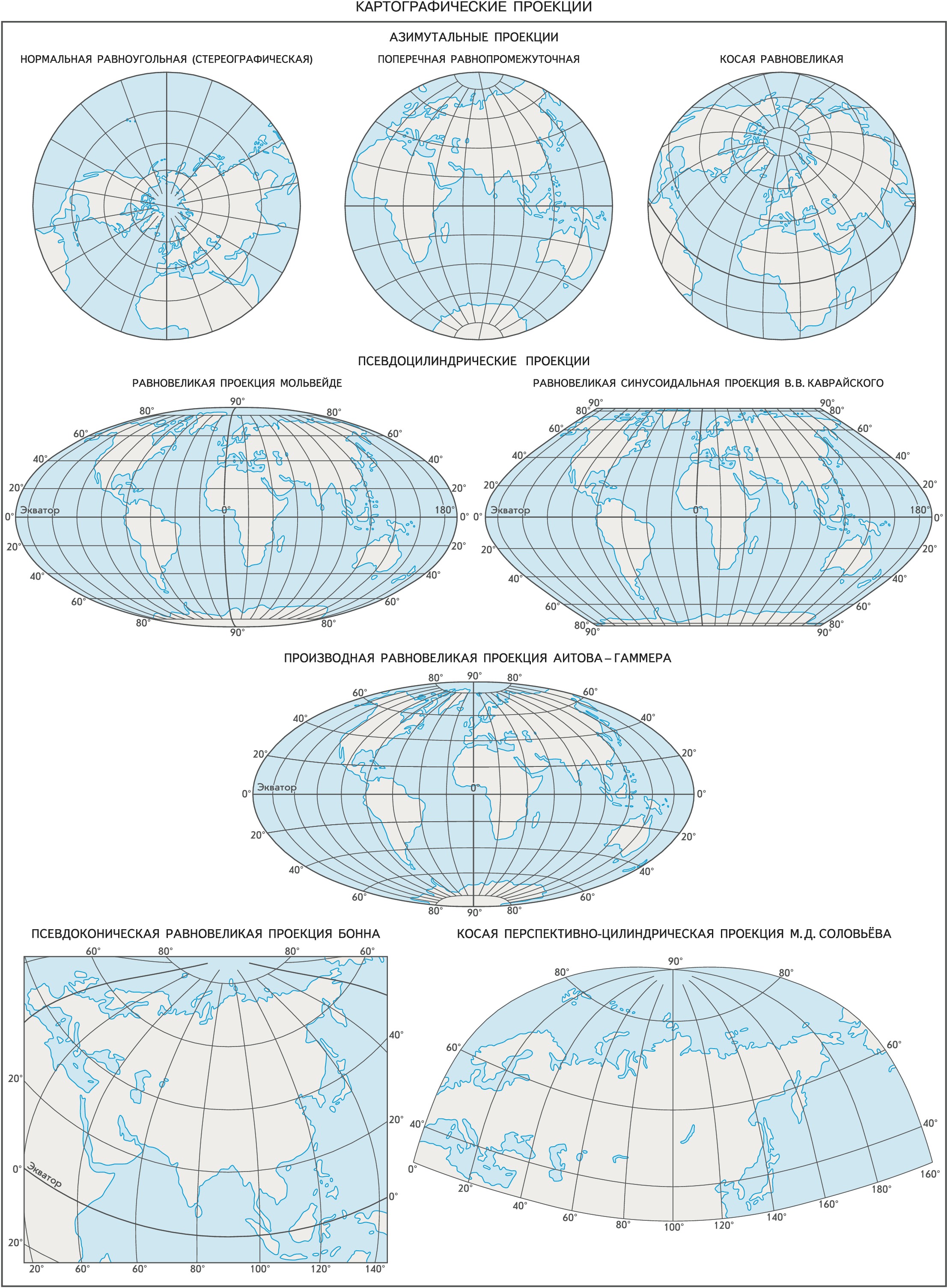
В зависимости от положения оси, используемой при проектировании системы сферич. координат, различают К. п. нормальные (ось сферич. координат совпадает с осью вращения Земли), поперечные (ось сферич. координат лежит в плоскости экватора) и косые (ось сферич. координат расположена под углом к плоскости экватора).
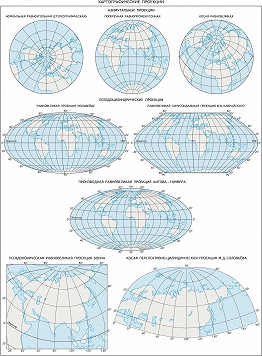
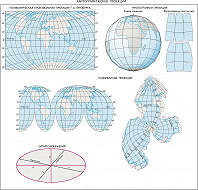
По виду нормальной сетки меридианов и параллелей выделяют цилиндрические К. п., в которых меридианы и параллели нормальной сетки являются прямыми, взаимно перпендикулярными линиями; иначе говоря, земной шар (эллипсоид) как бы проектируют на вспомогат. поверхность касательного или секущего цилиндра, который потом разворачивают в плоскость. В конических К. п. поверхность земного шара также проектируют на вспомогат. поверхность касательного или секущего конуса, поэтому в нормальной конич. проекции меридианы – это прямые, исходящие из точки полюса, а параллели – дуги концентрич. окружностей. В нормальных (полярных) азимутальных К. п. поверхность земного шара переносят на вспомогат. плоскость, перпендикулярную оси вращения Земли, параллели в ней – концентрич. окружности, а меридианы – диаметры этих окружностей. В этой проекции всегда картографируют полярные области. Если плоскость проекции перпендикулярна к плоскости экватора, то получается поперечная (экваториальная) азимутальная проекция, которую всегда используют для карт полушарий. Вспомогат. касательные поверхности дают одну общую линию или точку для эллипсоида (шара) и плоскости карты, где искажения отсутствуют. В случае секущей поверхности появляются две общие линии. В псевдоцилиндрических К. п. параллели – прямые (как и в цилиндрич. проекциях), средний меридиан – перпендикулярная им прямая, а остальные меридианы – кривые, увеличивающие кривизну по мере удаления от среднего меридиана. В псевдоконических К. п. все параллели предстают дугами концентрич. окружностей (как в нормальных конических), средний меридиан – прямая линия, а остальные меридианы – кривые, причём кривизна их возрастает с удалением от среднего меридиана. В нормальных поликонических К. п. параллели представлены дугами эксцентрич. окружностей, а меридианы – кривыми, симметричными относительно прямого среднего меридиана. Полярные псевдоазимутальные К. п. – это видоизменённые азимутальные проекции, в которых параллели изображены в виде концентрич. окружностей, а меридианы – в виде кривых линий, симметричных относительно одного или двух прямых меридианов.
Компьютерные технологии позволяют получать эти и множество произвольных К. п. любого вида. Их свойства задают в соответствии с особенностями картографируемой территории и её положением на земном шаре, назначением и способом использования карты, предпочтительным распределением искажений и т. п. Многогранные К. п. получают, проектируя земной шар на поверхность многогранника. Чаще всего каждая грань представляет собой равнобочную трапецию, хотя возможны и иные варианты (напр., шестиугольники, квадраты, ромбы). Разновидностью многогранных являются многополосные К. п., причём полосы могут «нарезаться» по меридианам и по параллелям. Такие проекции удобны тем, что искажения в пределах каждой грани или полосы невелики, поэтому их всегда используют для многолистных карт. Топографич. и обзорно-топографич. карты создают исключительно в многогранной проекции, и рамка каждого листа представляет собой сферич. трапецию, образованную линиями меридианов и параллелей. Однако блок листов карт нельзя совместить по общим рамкам без разрывов.
В некоторых случаях для уменьшения искажений используют разорванные К. п., где непрерывность изображения нарушается на океанах, если содержание карты приурочено к материкам (напр., карта населения, с.-х. карта), или на материках, если карта характеризует только океаны (напр., геологич. строение дна Мирового океана).
Многочисленность К. п. объясняется разнообразием задач, для которых служат карты (напр., для морских и аэронавигац. карт нужны равноугольные, а для кадастровых измерений – равновеликие К. п.), географич. положением территории (полярные области изображают в нормальных К. п., а полушария – в поперечных азимутальных К. п.), назначением карт (разные проекции нужны для школьных и научно-справочных карт). Созданы специальные электронные атласы К. п., с помощью которых можно отыскать подходящую К. п., оценить её свойства, а при необходимости провести те или иные модификации или преобразования. Выбор вариантов очень велик, но всё же существуют некоторые предпочтительные и наиболее традиционные картографич. проекции.
Карты мира обычно составляют в цилиндрич., псевдоцилиндрич. и поликонических К. п. Для уменьшения искажений часто используют секущие цилиндры, а псевдоцилиндрич. К. п. дают с разрывами на океанах. Карты полушарий всегда строят в азимутальных К. п. Для Зап. и Вост. полушарий используют поперечные (экваториальные), для Сев. и Юж. полушарий – нормальные (полярные), а в др. случаях (напр., для материкового и океанич. полушарий) – косые азимутальные К. п. Для карт материков Европы, Азии, Сев. Америки, Юж. Америки, Австралии с Океанией чаще всего применяют равновеликие косые азимутальные К. п., для Африки – поперечные, а для Антарктиды – нормальные азимутальные К. п. Карты России в целом составляют чаще всего в нормальных конич. равнопромежуточных К. п. с секущим конусом, но в некоторых случаях – в поликонич., произвольных и в других К. п. Однако сетка конич. К. п. не всегда удобна. Напр., на картах России для начальной школы требуется К. п., в которой меридианы сходятся в точке полюса, а самая сев. точка суши (мыс Челюскин) располагается ближе всего к сев. рамке. Карты отдельных стран, адм. областей, провинций, штатов выполняют в косых равноугольных и равновеликих конич. или азимутальных К. п., но многое зависит от конфигурации самой территории и её положения на земном шаре. Для небольших по площади районов задача выбора К. п. теряет актуальность, можно использовать разные равноугольные проекции, поскольку искажения площадей на малых территориях малоощутимы. Топографические карты России создают в поперечно-цилиндрич. проекции Гаусса – Крюгера, а карты США и мн. других зап. стран – в универсальной поперечно-цилиндрич. проекции Меркатора (сокр. UTM). Обе проекции близки по своим свойствам, и та и другая по существу являются многополосными. Морские и аэронавигационные карты выполняют исключительно в цилиндрич. проекции Меркатора, а тематич. карты морей и океанов создают в самых разнообразных, иногда довольно сложных проекциях. Напр., для совместного показа Атлантического и Сев. Ледовитого океанов применяют особые проекции с овальными изоколами, а для изображения Мирового ок. – равновеликие проекции с разрывами на материках.
В любом случае при выборе проекции, в особенности для тематич. карт, следует иметь в виду, что обычно искажения на карте минимальны в центре и быстро возрастают к краям. Кроме того, чем мельче масштаб карты и обширнее пространственный охват, тем большее внимание приходится уделять математич. факторам выбора К. п., и, наоборот, для малых территорий и крупных масштабов более существенными становятся географич. факторы.
Краткие исторические сведения
Первые карты с использованием сетки меридианов и параллелей создали греч. учёные Эратосфен, Гиппарх. Клавдий Птолемей в «Руководстве по географии» описал принципы создания некоторых конич. проекций. Великие географические открытия послужили значит. развитию картографии и способствовали созданию новых К. п. Большой вклад в теорию проекций внесли флам. картографы: Г. Меркатор, предложивший цилиндрическую (Меркатора) проекцию для навигац. карт, А. Ортелий, Я. Янсон (1588–1664) и др. Теория проекций всегда рассматривалась как важнейшая науч. проблема картографии. Свой вклад в разработку К. п. внесли известные математики И. Ламберт, Л. Эйлер, Ж. Лагранж, К. Гаусс. В сер. 19 в. франц. исследователь А. Тиссо создал общую теорию искажений К. п. В России теорией К. п. занимались А. П. Болотов (1803–1853), Ф. И. Шуберт, П. Л. Чебышев, Д. А. Граве, Д. И. Менделеев, В. В. Витковский (1856–1924), Ф. Н. Красовский, В. В. Каврайский, Г. А. Гинзбург (1905–1975), Н. А. Урмаев и др.