КАТАСТРО́Ф ТЕО́РИЯ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
КАТАСТРО́Ф ТЕО́РИЯ, математич. описание катастроф – скачкообразных изменений, возникающих в виде внезапного ответа системы на плавное изменение внешних условий; даётся теориями особенностей дифференцируемых (гладких) отображений X. Уитни и бифуркаций А. Пуанкаре и А. А. Андронова. Название введено Р. Томом в 1972. К. т. используется в геометрич. и физич. оптике, в теории элементарных частиц, в гидродинамике при расчётах устойчивости кораблей, в геологии, биологии, социологии, экономике, лингвистике, а также в медицине при исследовании биений сердца и психич. расстройств, при моделировании деятельности мозга и т. д. Теория особенностей применяется, когда явление описывается гладким отображением и нет причин для нетипичности (напр., симметрии).
Теория особенностей обобщает исследование экстремумов функций на случай нескольких функций любого числа переменных. Критич. точкой функции $y$ называется точка, в которой все первые частные производные равны нулю, $\partial y/ \partial x_i=0$; критич. точка называется невырожденной, если матрица $\partial^2 y/ \partial x_i \partial x_j$ невырождена, т. е. её определитель отличен от нуля. У типичной функции все критич. точки невырождены. Любая гладкая функция в окрестности каждой невырожденной критич. точки приводится к одной из т. н. нормальных форм Морса, $y=\pm x^2_1 \pm \ldots \pm x^2_n +C$, гладкой заменой независимых переменных. Эти невырожденные особенности устойчивы: напр., всякая функция, достаточно близкая к $y=x^2$ (с производными), имеет в подходящей точке вблизи нуля подобную же особенность (невырожденную точку минимума). Все более сложные особенности неустойчивы. Напр., вырожденная критич. точка функции $y=x^3$ в нуле распадается на две критич. точки при возмущении, превращающем $x^3$ в $x^3- \varepsilon x$.
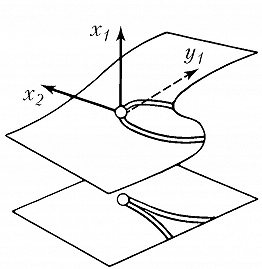
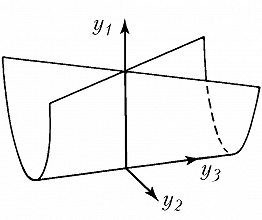
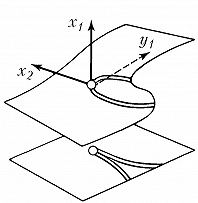
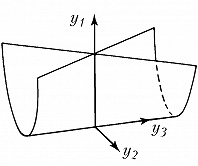
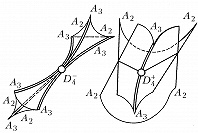
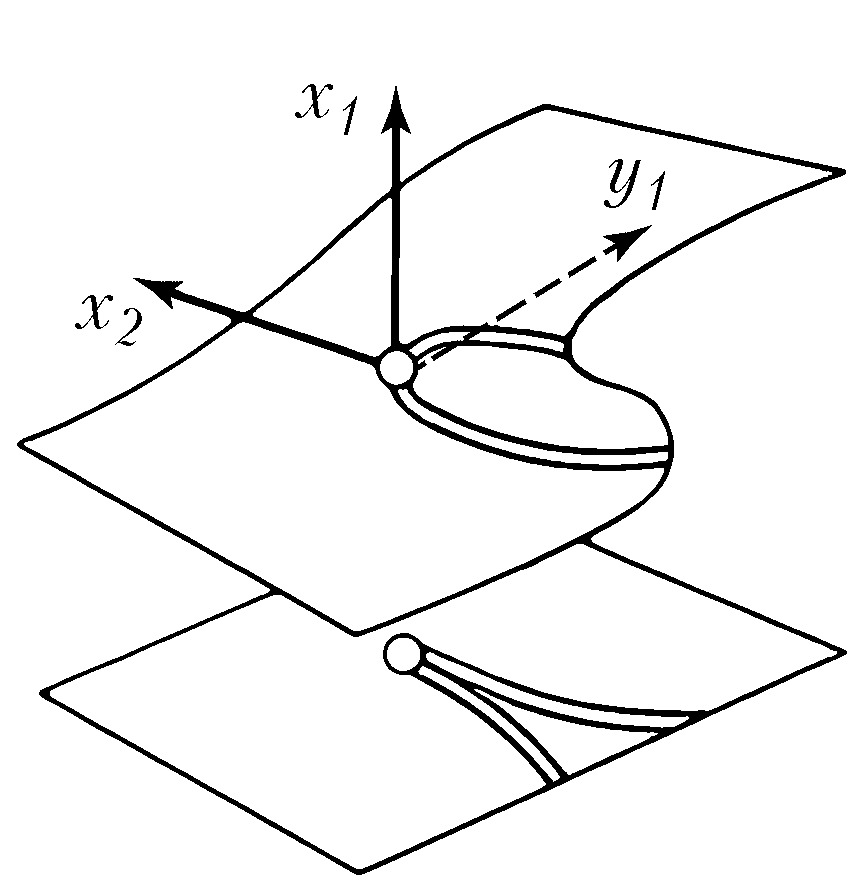
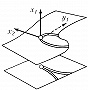
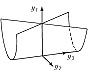
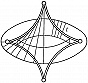
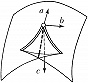
Типичные отображения поверхности на плоскость $(R^2 \to R^2)$ также имеют лишь устойчивые особенности, а именно складку $(y_1=x^2_1, y_2=x_2)$ либо сборку Уитни $(y_1=x^3_1 +x_1x_2, y_2=x_2)$. Сборка есть особенность проецирования поверхности $y_1=x^3_1+x_1x_2$ из пространства $(x_1, x_2, y_1)$ на плоскость $(y_1, x_2)$ (рис. 1). Списки типичных особенностей отображений $R^3 \to R^3$ и $R^4 \to R^4$ таковы: 1) $y_1=x^2_1, y_i=x_i (i>1)$; 2) $y_1=x^3_1+x_1x_2, y_i=x_i (i>1)$; 3) $y_1=x^4_1+x^2_1x_2+x_1x_3, y_i=x_i (i>1)$; 4) $y_1=x^2_1 \pm x^2_2+x_1x_3+x_2x_4, y_2=x_1x_2, y_3=x_3, y_4=x_4$; 5) $y_1=x^5_1+x_1^3x_2+x_1^2x_3+x_1x_4, y_i=x_i (i>1)$. Отображение $R^2 \to R^3$ обычно имеет особенностями лишь «зонтики» Уитни – Кэли (рис. 2; $y_1=x_1^2, y_2=x_1x_2, y_3=x_2$). При переходе к высшим размерностям списки типичных особенностей растут и даже становятся континуальными (напр., не всякое отображение $R^n \to R^n$ при $n>8$ аппроксимируется устойчивым). Число классов топологически различных особенностей остаётся конечным при любых размерностях.
В теории бифуркаций рассматривается динамическая система, описываемая уравнением $\dot {x}=\theta(x, \varepsilon)$, c заданным векторным полем $\theta$ в $n$-мерном фазовом пространстве {$x$}. Поле зависит от $k$-мерного параметра $\varepsilon$. Множество состояний равновесия определяет в ($n+k$)-мерном пространстве {$x, \varepsilon$ } $k$-мерную поверхность $\theta(x,\varepsilon)=0$. В типичном случае эта поверхность гладкая, но её проекция на пространство «управляющих параметров» {$\varepsilon$} может иметь особенности. Если рассматривать значения {$\varepsilon$} как функции на поверхности состояний равновесия, то точки, в которых якобиан этих функций равен 0, называются бифуркационными, а значения функций в этих точках – бифуркационными значениями параметров $\varepsilon$. При подходе управляющих параметров к бифуркационным значениям положения равновесия «бифурцируют» (рождаются или умирают). Знание геометрии типичных особенностей позволяет описывать происходящие при этом явления, напр. скачкообразный переход системы к далёкому состоянию равновесия при плавном изменении параметров. Такие скачки способны разрушить систему (механич., упругую, электрическую, биологич., химич. и др.), откуда и назв. «теория катастроф».
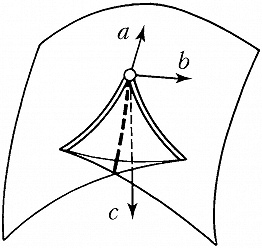
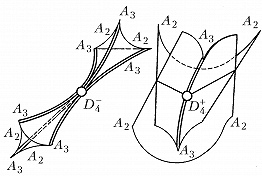
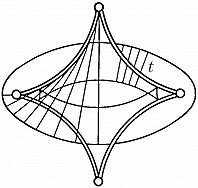
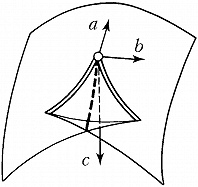
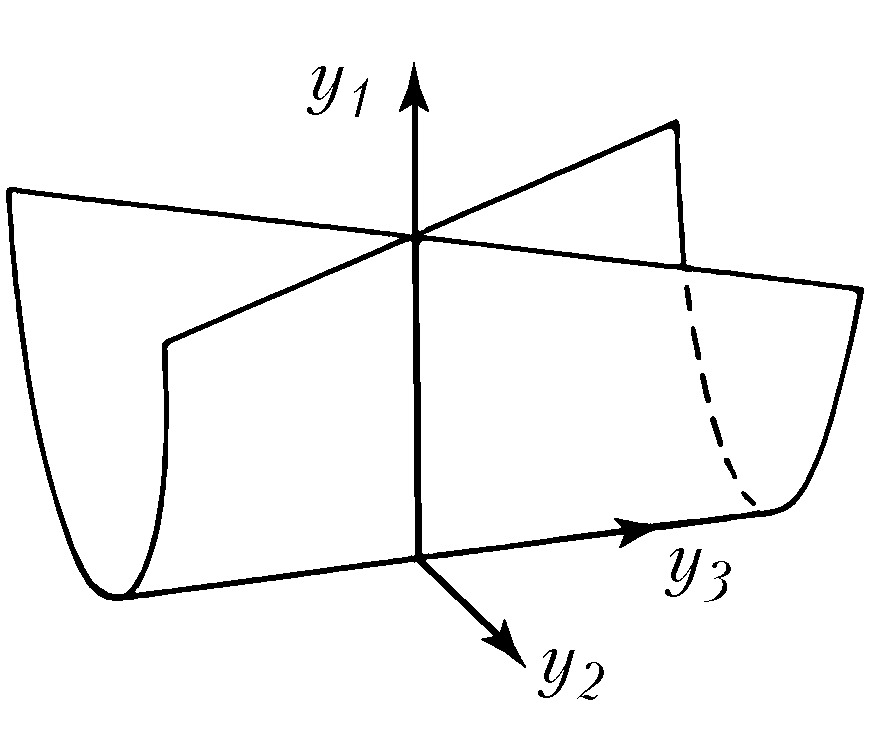
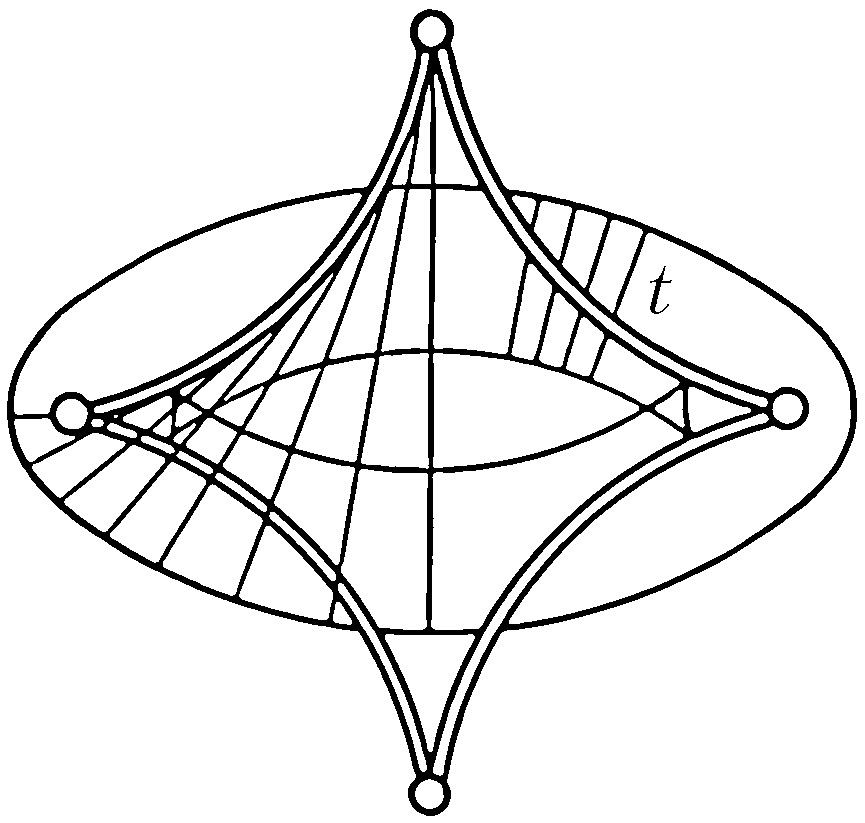
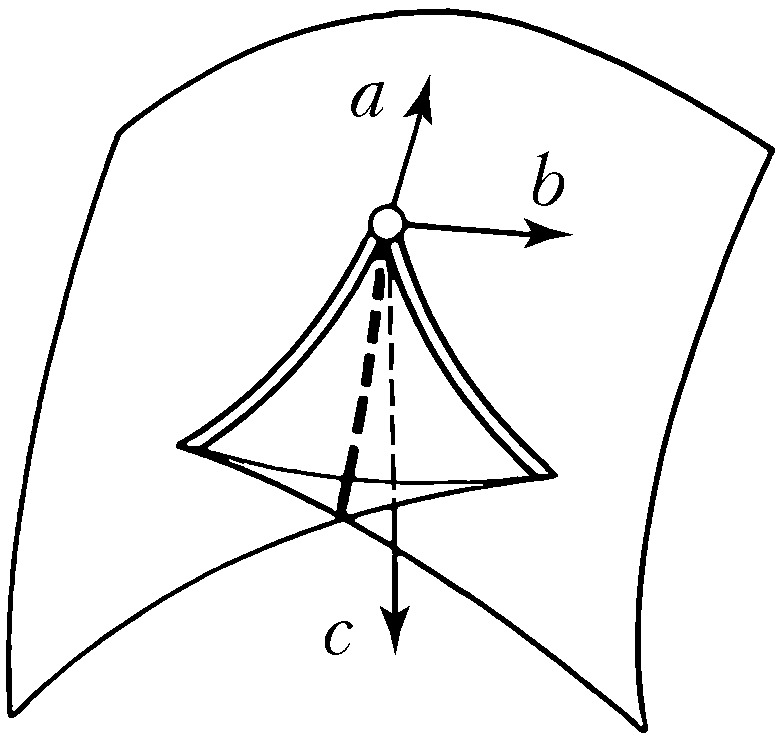
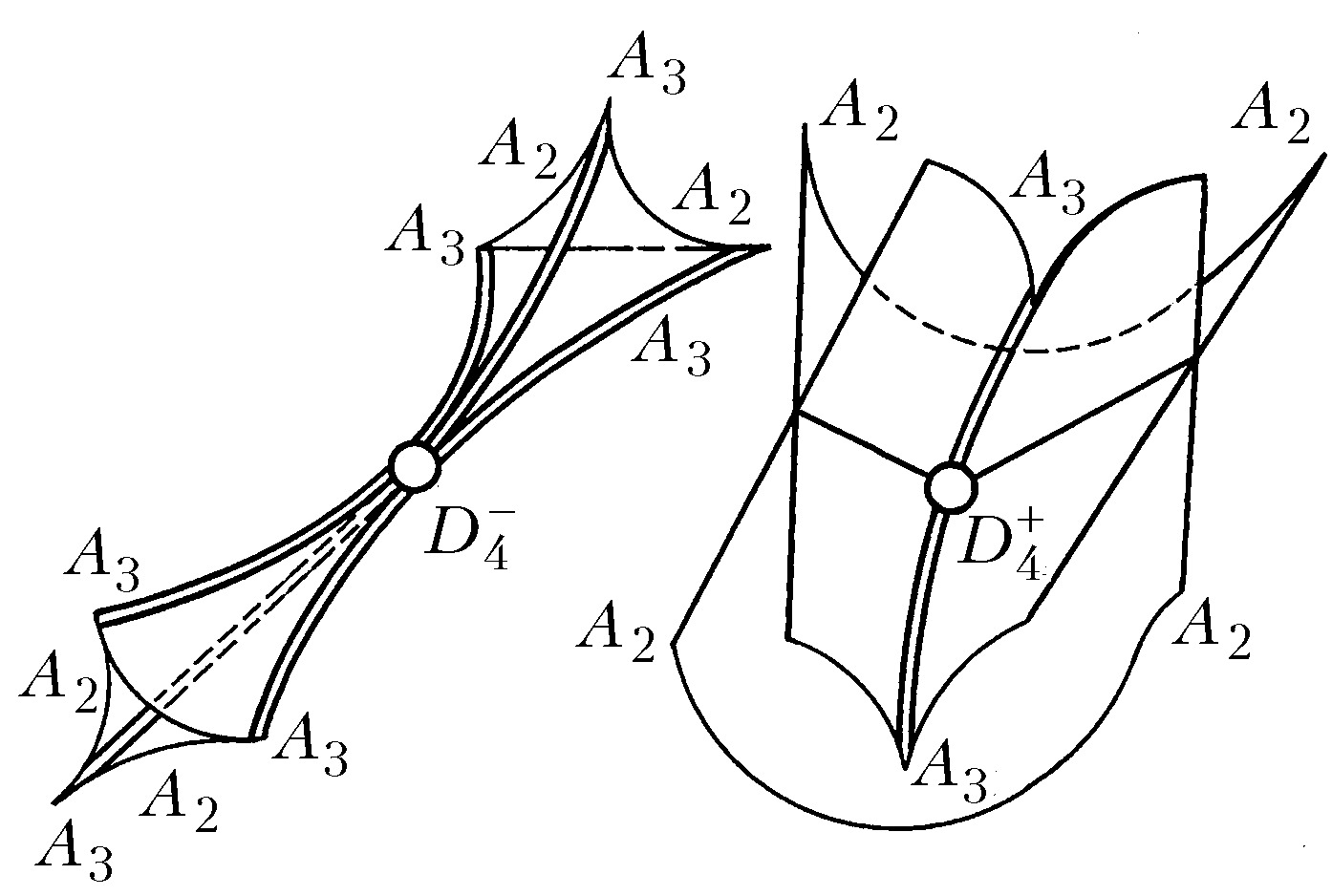
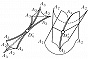
Наибольший успех достигнут в приложениях К. т. к оптике, где не были известны даже типичные особенности каустик (см. Каустическая поверхность) и перестройки волновых фронтов в трёхмерном пространстве. Рассмотрим возмущение (свет, звук, ударную волну, эпидемию и др.), распространяющееся с единичной скоростью из области, ограниченной гладким фронтом. Чтобы построить фронт через время $t$, нужно отложить отрезок длиной $t$ на каждом луче нормали. Через некоторое время на движущемся фронте появляются особенности в точках каустики (огибающей семейства лучей) исходного фронта. Напр., при распространении возмущения на плоскости внутрь эллипса особенности фронта скользят по каустике, имеющей 4 точки возврата (рис. 3). Эти особенности устойчивы (не исчезают при малой деформации исходного фронта). Типичные особенности фронтов в трёхмерном пространстве – это самопересечения, рёбра возврата (нормальная форма $x^2=y^3$) и ласточкины хвосты [рис. 4; эта поверхность образована точками $(a,b,c)$, для которых многочлен $x^4+ax^2+bx+c$ имеет кратный корень]. Каустики в трёхмерном пространстве имеют особенности ещё двух видов (пирамида и кошелёк; рис. 5).
Почти все особенности волновых фронтов можно описать как множества бифуркационных значений параметра $\mu$, при которых возникают особенности отображения $(x, \mu)\to \mu$ гиперповерхности $F(x, \mu)=0$ в пространство $\mu$, где $F$ – типичное семейство гладких функций вектора $x$ и векторного параметра $\mu$. Типичные особенности каустик (или градиентных отображений $x \to \partial S/ \partial x$, или отображений Гаусса, сопоставляющих точке поверхности направление нормали) можно описать как множества бифуркационных значений параметра $\mu$, при которых функция $F(x, \mu)$ переменной $x$ имеет вырожденную критич. точку. Ласточкин хвост, пирамида и кошелёк получаются при $$\begin{gather} F=x^5+ \mu_1x^3+ \mu_2x^2+ \mu_3x;\\ F=x_1^2x_2 \pm x_2^3+ \mu_1x_2^2+ \mu_2x_2+ \mu_3 x_1. \end{gather}$$
Особенностям каустик и фронтов геометрич. оптики соответствуют в волновой теории особенности асимптотик осциллирующих интегралов в методе стационарной фазы или в многомерном перевала методе при слиянии нескольких стационарных точек. При подходе к точке каустики интеграл возрастает в $\lambda^{-\nu}$ раз, где $\lambda$ – длина волны, а показатель $\nu$ равен: 1/6 для общей точки каустики ($A_2$, особенность Эйри); 1/4 для общей точки ребра возврата ($A_3$, особенность Пирси); 3/10 для ласточкина хвоста (особенность $A_4$); 1/3 для кошелька и пирамиды (особенности $D_4$). Эти особенности связаны с простыми группами Ли $A_k \sim SU(k+1)$, $D_k \sim O(2k)$, а также с правильными многогранниками [конечными подгруппами группы $SU(2)$]. Показатель $\nu$ определяет интенсивность света вблизи каустики и её особенности, разрушение среды интенсивной волной, скопление частиц при движении пылевидной среды с потенциальным полем скоростей (с иным значением $\nu$) и т. п. Универсальность геометрии бифуркационных диаграмм позволяет использовать их для моделирования мн. различных по своему физич. смыслу явлений.