МА́КСВЕЛЛА РАСПРЕДЕЛЕ́НИЕ

МА́КСВЕЛЛА РАСПРЕДЕЛЕ́НИЕ, функ­ция рас­пре­де­ле­ния по ско­ро­стям мик­рочас­тиц (ато­мов или мо­ле­кул) мак­ро­ско­пич. фи­зич. сис­те­мы, на­хо­дя­щей­ся в те­п­ло­вом рав­но­ве­сии со сво­им ок­ру­же­ни­ем при за­дан­ной аб­со­лют­ной тем­пе­ра­ту­ре Т в от­сут­ст­вие внеш­не­го по­ля. М. р. спра­вед­ли­во для час­тиц, опи­сы­вае­мых в рам­ках клас­сич. ме­ха­ни­ки, при­чём оно не за­ви­сит от взаи­мо­дей­ст­вия ме­ж­ду час­ти­ца­ми и обу­слов­ле­но лишь на­ли­чи­ем вза­им­ных столк­но­ве­ний ме­ж­ду ни­ми; в ча­ст­но­сти, М. р. име­ет ме­сто для бро­унов­ско­го дви­же­ния час­тиц, взве­шен­ных в жид­ко­сти или га­зе.

В слу­чае мно­го­атом­ных мо­ле­кул М. р. от­но­сит­ся толь­ко к по­сту­па­тель­но­му дви­же­нию цен­тров инер­ции мо­ле­кул и не за­ви­сит ни от вра­ща­тель­ных дви­же­ний мо­ле­ку­лы как це­ло­го, ни от внут­ри­мо­ле­ку­ляр­ных ко­ле­ба­тель­ных дви­же­ний.

М. р. мо­жет быть за­пи­са­но в разл. фор­мах – напр., для де­кар­то­вых ком­по­нент ско­ро­стей час­тиц или их от­но­сит. ско­ро­стей. Наи­бо­лее упот­ре­би­тель­ной фор­мой М. р. яв­ля­ет­ся рас­пре­де­ле­ние $F(v)$ по аб­со­лют­ной ве­ли­чи­не (мо­ду­лю) ско­ро­стей час­тиц $v$. Чис­ло час­тиц $dw(v)$, имею­щих ве­ли­чи­ну ско­ро­сти в ин­тер­ва­ле от $v$ до $v+dv$, да­ёт­ся вы­ра­же­ни­ем: $$dw(v)=F(v)dv=n(m/2πkT)^{3/2}\exp[–mv^2/2kT]4πv^2dv,$$ где $n$ – кон­цен­тра­ция час­тиц ($n=\textrm{const}$ в от­сут­ст­вие внеш­них по­лей), $m$ – мас­са час­ти­цы ($m=\textrm{const}$ при не­ре­ля­ти­ви­ст­ских ско­ро­стях час­тиц), $k$ – по­сто­ян­ная Больц­ма­на.

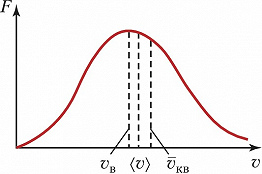
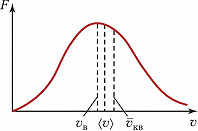
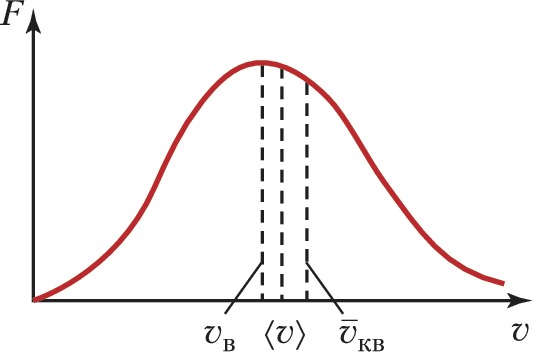
С ма­те­ма­тич. точ­ки зре­ния М. р. яв­ля­ет­ся нор­маль­ным рас­пре­де­ле­ни­ем Га­ус­са (рис.), при по­мо­щи ко­то­ро­го мож­но вы­чис­лить ср. зна­че­ние лю­бой функ­ции от ско­ро­сти час­тиц $v$, в т. ч. наи­бо­лее ве­ро­ят­ную ско­рость $v_в=(2kT/m)^{1/2}$, ср. ско­рость $⟨v⟩=(8kT/πm)^{1/2}$ и ср. квад­ра­тич­ную ско­рость $\bar v_{кв}=⟨v^2⟩^{1/2}= (3kT/m)^{1/2}$. Так, для мо­ле­ку­лы $Н_2$ при $Т=273 К$ $v_в$ со­став­ля­ет ок. 1500 м/с и по по­ряд­ку ве­ли­чи­ны сов­па­да­ет со ско­ро­стью зву­ка в га­зе.

М. р. ус­та­нов­ле­но Дж. К. Мак­свел­лом

в 1859. Пер­во­на­чаль­но при его вы­во­де Мак­свелл ис­хо­дил из об­щих свойств со­стоя­ния те­п­ло­во­го рав­но­ве­сия, в ко­то­ром от­сут­ст­ву­ют мак­ро­ско­пич. по­то­ки час­тиц, так что ус­та­но­вив­шее­ся рас­пре­де­ле­ние по ско­ро­стям долж­но быть од­но­род­ным и изо­троп­ным. Позд­нее Мак­свелл дал бо­лее стро­гое обос­но­ва­ние М. р., рас­смот­рев в ка­че­ст­ве фи­зич. ме­ха­низ­ма про­цес­са ус­та­нов­ле­ния это­го со­стоя­ния («тер­ма­ли­за­ции») вза­им­ные столк­но­ве­ния ме­ж­ду час­ти­ца­ми, под­чи­няю­щие­ся де­таль­но­го рав­но­ве­сия прин­ци­пу

 >>

. М. р. по­лу­чи­ло пря­мое экс­пе­рим. под­твер­жде­ние в опы­тах О. Штер­на

 >>

с мо­ле­ку­ляр­ны­ми пуч­ка­ми (1920) и в опы­тах Штер­на и др. (1947).

С фи­зич. точ­ки зре­ния М. р. яв­ля­ет­ся од­ним из ста­цио­нар­ных ре­ше­ний ки­не­тич. урав­не­ния Больц­ма­на и ча­ст­ным слу­ча­ем рас­пре­де­ле­ния Мак­свел­ла – Больц­ма­на (см. Больц­ма­на рас­пре­де­ле­ние

), ко­то­рое обоб­ща­ет М. р. на слу­чай на­ли­чия не­од­но­род­но­го внеш­не­го по­ля ($n≠\textrm{сonst}$). Наи­бо­лее об­щим ве­ро­ят­но­ст­ным рас­пре­де­ле­ни­ем час­тиц по их пол­ным энер­ги­ям яв­ля­ет­ся Гиб­бса рас­пре­де­ле­ние

 >>

, обоб­щаю­щее М. р. на слу­чай на­ли­чия как внеш­не­го по­ля, так и взаи­мо­дей­ст­вия ме­ж­ду час­ти­ца­ми.

При по­ни­же­нии тем­пе­ра­ту­ры $T$ или по­вы­ше­нии кон­цен­тра­ции час­тиц $n$ ста­но­вит­ся не­об­хо­ди­мым кван­то­вое опи­са­ние по­сту­па­тель­но­го дви­же­ния ато­мов и мо­ле­кул. М. р. мож­но рас­смат­ри­вать как пре­дель­ный слу­чай кван­то­вых рас­пре­де­ле­ний: Бо­зе – Эйн­штей­на рас­пре­де­ле­ния

 и Фер­ми – Ди­ра­ка рас­пре­де­ле­ния

 >>

, в ус­ло­ви­ях, ко­гда мож­но пре­неб­речь яв­ле­ни­ем кван­то­во­го вы­ро­ж­де­ния иде­аль­но­го га­за.