МАГНИ́ТНАЯ ГИДРОДИНА́МИКА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
МАГНИ́ТНАЯ ГИДРОДИНА́МИКА, раздел физики, изучающий поведение проводящих жидкостей или газов в магнитном поле и динамику самого магнитного поля, связанную с их движением. Объектами изучения М. г. служат электролиты, жидкие металлы, электропроводящие взвеси и расплавы, плазма. Появление термина «М. г.» и оформление М. г. в самостоят. науку связывают с именем Х. Альвена, хотя исторически первые магнитогидродинамич. эффекты (МГД-эффекты) были обнаружены и исследовались ещё в 19 в. М. Фарадеем. Осн. МГД-явления связаны с генерацией электрич. токов в проводящей жидкости, движущейся в магнитном поле, возникновением силы Ампера, действующей на жидкость, и результирующим изменением самого магнитного поля. Поэтому динамика жидкости и магнитного поля в рамках М. г. рассматривается согласованно.
Эффекты, изучаемые М. г., используются в беспоршневых электромагнитных насосах, магнитогидродинамических генераторах, плазменных ускорителях и двигателях, МГД-компрессорах и аналогичных устройствах. М. г. описывает процессы, происходящие в звёздах, магнитосферах планет, джетах и аккреционных дисках (см. Аккреция), что составляет предмет космической магнитогидродинамики.
М. г. относится к числу локальных полевых теорий, в которых состояние среды описывается скалярными и векторными величинами (полями), заданными как функции координат и времени и связанными между собой локальными уравнениями, в которые входят только сами величины и их производные. Стандартный набор величин включает плотность жидкой среды $ρ$, массовую скорость $\boldsymbol v$, давление (скаляр $p$ или тензор $\boldsymbol P$), магнитную индукцию $\boldsymbol B$. Различают идеальную М. г., в рамках которой можно пренебречь вязкостью и электрич. сопротивлением жидкости, и диссипативную, в которой эти эффекты учитываются. Наиболее ярко МГД-эффекты проявляются в хорошо проводящих средах, которые в определённых условиях можно рассматривать как идеальные.
Идеальная магнитная гидродинамика
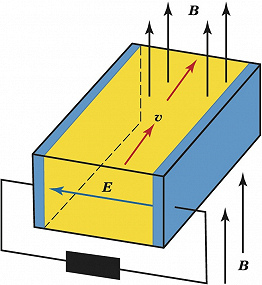
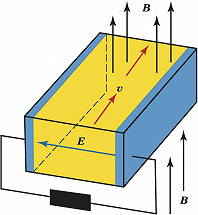
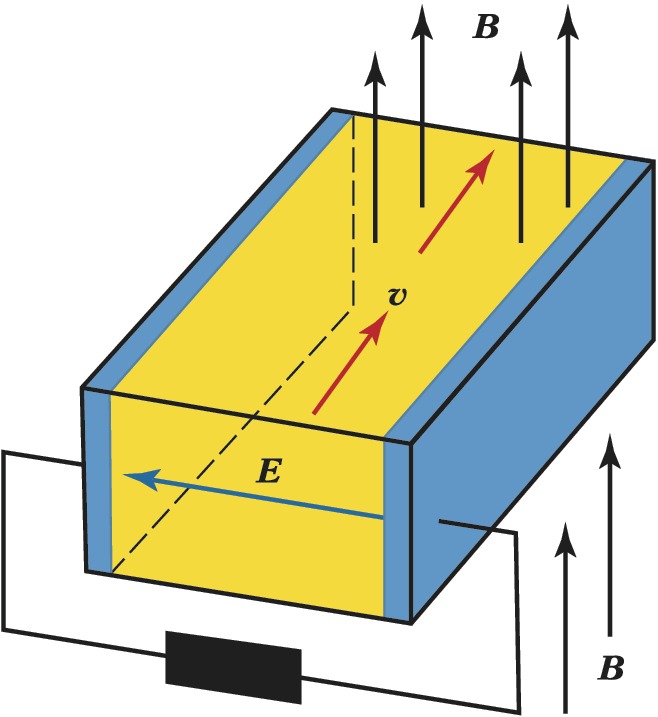
использует гидродинамич. уравнение непрерывности $$∂ρ/∂t + \textrm{div}(ρ\boldsymbol v) = 0,\tag1$$уравнение движения (Эйлера)$$ρ∂v/∂t + ρ(\boldsymbol v∇)\boldsymbol v + ∇p = [\boldsymbol j \boldsymbol B/c],\tag2$$правая часть которого представляет силу Ампера, и уравнение динамики магнитного поля$$∂\boldsymbol B/∂t =\textrm{rot}[\boldsymbol v\boldsymbol B],\tag3$$ часто называемое «уравнением вмороженности» (здесь и далее используется система единиц СГС; $\boldsymbol j$ – плотность электрич. тока, $c$ – скорость света). Система уравнений (1)–(3) дополняется уравнением для давления; при адиабатич. движении применяют уравнение адиабаты с показателем $γ$$$∂p/∂t + (\boldsymbol v∇)p + γp \textrm{div}\boldsymbol v = 0.\tag4$$ Основное для М. г. уравнение (3) – это уравнение Максвелла, выражающее закон электромагнитной индукции Фарадея с учётом приближённого (с точностью до членов порядка $v^2/c^2$) отсутствия электрич. поля $\boldsymbol E′$ в собств. системе отсчёта идеально проводящей жидкости (с проводимостью $σ→∞$),$$\boldsymbol E′≈ \boldsymbol E + [\boldsymbol v\boldsymbol B/c] ≈ \boldsymbol j/σ → 0.\tag5$$ Формула (5) позволила в нерелятивистском пределе ($v^2/c^2≪1$) пренебречь в уравнении (2) электрической (кулоновской) силой по сравнению с силой Ампера и вкладом токов смещения в циркуляцию магнитного поля, т. е. полагать $\boldsymbol j ≈ c\, \textrm{rot}\boldsymbol B/4π$, что замыкает систему идеальных МГД-уравнений (1)–(4). В соответствии с формулой (5) при протекании проводящей жидкости поперёк магнитного поля в ней возникает электрич. поле $\boldsymbol E$ (объёмная эдс) и, наоборот, прикладываемое внешнее электрич. поле вызывает движение жидкости (рис. 1). На этом принципе основана работа МГД-насосов, измерителей скоростей, МГД-генераторов и др.
Вмороженность магнитного поля
Уравнение (3) аналогично уравнению для вектора завихрённости изоэнтропийной или изотермич. жидкости в обычной гидродинамике (вектор $\boldsymbol B$ играет роль $\textrm{rot}\,\boldsymbol v$), для которого также используется термин «вмороженность». Суть этого термина заключается в представлении о вмороженности силовых линий магнитного поля в частички жидкости, так что движение среды увлекает за собой магнитное поле и, наоборот, сжатие или растяжение силовых линий магнитного поля приводит к сжатию или расширению среды. Следствием уравнения вмороженности (3) является то, что циркуляция магнитного поля по контуру, движущемуся и деформируемому вместе с жидкой средой, и поток магнитного поля через этот контур постоянны во времени. Отсюда следует, что в идеальной М. г. топология магнитного поля не меняется, т. е. силовые линии магнитного поля, замкнутые или намотанные на некоторую тороидальную поверхность, остаются такими же в процессе эволюции. Они могут лишь деформироваться (сжиматься или растягиваться), но не могут рваться или замыкаться друг на друга (перезамыкание – признак существенной резистивности среды).
Магнитные силы
Сила Ампера в уравнении (2) приводит к появлению силы изотропного магнитного давления $\boldsymbol B^2/8π$, которое добавляется к обычному газокинетич. давлению среды $p$, и силы магнитного натяжения $(\boldsymbol B∇)\boldsymbol B/4π$. Эти силы способны удерживать неподвижную проводящую жидкость в магнитном поле, обеспечивая её равновесие. Дополнит. упругие напряжения в МГД-средах способствуют возникновению новых типов колебаний, к которым относятся альвеновские волны – поперечные к направлению вектора $\boldsymbol B$ смещения среды, распространяющиеся вдоль магнитного поля, и магнитозвуковые волны – продольные волны, распространяющиеся перпендикулярно магнитному полю (см. также Волны в плазме). Определённую специфику имеют и ударные МГД-волны, отличающиеся от обычных ударных волн тем, что после прохождения фронта волны элементы среды получают касательный импульс за счёт магнитных напряжений.
Диссипативная магнитная гидродинамика
Для описания свойств реальных диссипативных сред вместо уравнения Эйлера (2) используют Навье – Стокса уравнение. Для несжимаемой жидкости в правую часть уравнения (2) добавляют член $v∇^2\boldsymbol v$, описывающий вязкость; при этом в правую часть (3) нужно добавить аналогичный «вязкий», или диффузионный, член $v_м∇^2\boldsymbol B$, где $v$ – обычная кинематич. вязкость, $v_м = с^2/4πσ$ – магнитная вязкость, называемая также коэф. диффузии магнитного поля. Отношение $v/v_м = Pr_м$ (магнитное число Прандтля) для большинства МГД-сред много меньше единицы, поэтому именно конечная проводимость среды является первоочередным фактором, приводящим к отклонению от идеальности. Добавленный в уравнение (3) диффузионный член объясняет просачивание магнитного поля в проводящую среду за время $t$ на характерную «скиновую» длину порядка $(v_мt)^{1/2}$. Отношение $Re_м = Lv/v_м = 4πσLv/c^2$ конвективного члена к диффузионному в уравнении для магнитного поля по аналогии с числом Рейнольдса в гидродинамике называют магнитным числом Рейнольдса ($L$ и $v$ – характерные размер и скорость движения среды).
В лабораторных условиях часто реализуется случай $Re_м ≪ 1$, когда течение проводящей среды слабо искажает магнитное поле, поэтому его можно считать заданным внешними источниками, а индуцированные магнитные поля не рассматривать (т. н. гальванич. приближение). Вместе с тем наводимый в среде ток, взаимодействуя с внешним магнитным полем, приводит к МГД-эффектам. Регулируя протекающий ток, можно создавать регулируемую выталкивающую (архимедову) силу, которая действует на помещённые в проводящую жидкость тела. Этот эффект лежит в основе принципа МГД-сепарации.
В противоположном пределе $Re_м ≫ 1$ среда становится практически идеальной. Этот предел реализуется не только при очень высокой проводимости, но и в случае больших размеров и скоростей системы, что характерно для астрофизич. задач (см. Космическая магнитогидродинамика). В этом случае при долговременной эволюции системы в результате конвективного перемешивания и редкого пересоединения магнитных силовых линий система способна «забыть» исходную магнитную конфигурацию.
Учёт конечной диссипации особенно важен в окрестностях замкнутых магнитных силовых линий сильного поля, в частности в окрестности линий, на которых поле обращается в нуль. В таких областях образуются тонкие токовые слои и идеальная М. г. принципиально неприменима, т. к. в этих слоях происходит процесс пересоединения магнитных силовых линий. При пересоединении противоположно направленных силовых линий возможно высвобождение магнитной энергии и превращение её в иные формы энергии. Такой процесс может приводить к хромосферным вспышкам на Солнце и суббурям в земной атмосфере, а в плазме тороидальных магнитных систем вблизи замкнутых силовых линий возникает тиринг-неустойчивость, ведущая к расщеплению плазмы на семейство магнитных островов. Необходимость учёта диссипативности может быть вызвана граничными условиями, как, напр., в случае МГД-течения в канале. Ширина переходного слоя, формируемого вблизи стенок плоского канала, перпендикулярного направлению магнитного поля, определяется магнитной вязкостью и обратно пропорциональна числу Гартмана $Ha = LB(σ /ρvc^2)^{1/2}$, которое равно отношению силы Ампера к силе вязкости и характеризует тип течения в М. г. При $Ha ≫ 1$ (т. н. течение Гартмана) даже при весьма умеренном магнитном поле скорость быстро нарастает при удалении от стенки канала и практически однородна в его объёме. При $Ha ≪ 1$ влияние магнитного поля малó и течение переходит в обычное течение Пуазёйля.
Гидромагнитное динамо –
классич. задача слабодиссипативной М. г., заключающаяся в поиске такого ламинарного течения проводящей среды, которое могло бы создавать, усиливать и поддерживать магнитное поле в этой среде, как, напр., в случае звёзд и планет. Эта задача часто рассматривается в приближении слабого поля, когда влиянием магнитных напряжений на течение среды можно пренебречь (кинематич. динамо). Стационарное поддержание поля возможно лишь при определённых значениях скорости и магнитного числа Рейнольдса, а абсолютная величина магнитного поля не имеет значения, т. е. магнитное динамо может существовать при любом уровне затравочного магнитного поля. Хотя магнитные поля звёзд и планет являются преим. осесимметричными, они не могут поддерживаться только чисто осесимметричными течениями (теорема Каулинга, 1934). Угловая скорость осесимметричного вращения при осесимметричном магнитном поле, не имеющем азимутальной составляющей, должна быть постоянной на силовой линии (закон изоротации Ферраро, 1937). Принципиального запрета на возникновение динамо-эффекта при спец. распределении скоростей среды нет, построены подтверждающие примеры, однако полная теория динамо, описывающая самозарождение магнитного поля и соответствующее распределение скоростей с учётом всех действующих сил, пока ещё не создана.
Течение проводящей среды может быть и турбулентным. Источником МГД-турбулентности являются и обычные гидродинамич. неустойчивости, и магнитогидродинамические неустойчивости, связанные с магнитным полем и его неоднородностью. Для МГД-турбулентности характерно присутствие как прямого (от крупных масштабов к мелким), так и обратного каскадов, в результате чего могут возникнуть крупномасштабные гидродинамич. структуры на фоне широкого спектра мелкомасштабных осцилляций. Крупномасштабное движение может сопровождаться генерацией макроскопич. полей, тогда говорят о турбулентном динамо. Для адекватного моделирования МГД-турбулентности необходимы согласованные расчёты течения жидкости и динамики магнитного поля. Однако полное трёхмерное моделирование МГД-процессов – весьма сложная и пока не вполне выполнимая задача, в первую очередь из-за больших различий пространственных и временны́х масштабов характерных процессов. Поэтому систему МГД-уравнений упрощают, уменьшая её порядок. Для этого разделяют физич. степени свободы системы при сосуществовании быстрых и медленных движений. В некоторых случаях возможно использование приближения слабого поля, когда изменения поля рассчитываются при заданном движении среды. В приближении сильного поля определяющими являются магнитные натяжения, что может быть характерно для разреженных атмосфер звёзд и планет. Локальная плотность магнитной энергии достигает больших величин, и возмущения магнитного поля способны приводить к мощным перемещениям сгустков вещества (напр., выбросы и протуберанцы на Солнце, стримеры в термоядерных устройствах). Пример поля скоростей, образующегося в магнитной термоядерной системе в результате длительной турбулентной эволюции, приведён на рис. 2.
Многожидкостная магнитная гидродинамика
Одножидкостная М. г., описывающая проводящую жидкость, имеет ряд ограничений. Для плазмы, содержащей разные группы заряженных частиц, более естественным является многожидкостное МГД-описание, в рамках которого каждая компонента плазмы рассматривается как отд. жидкость со своими плотностью, скоростью и давлением. Формулы вида (1), (2) возникают как уравнения для суммарной плотности и среднемассовой скорости всех компонент плазмы. Необходимое для гидродинамич. описания упорядочение, обеспечивающее локальность связей между моментами (напр., между давлением и потоками тепла), достигается в случае сильностолкновительной плазмы, в которой время между столкновениями и длина свободного пробега частиц малы по сравнению с характерным временем процесса и размером неоднородности плазмы; при этом давление можно считать практически изотропным. В случае редких столкновений необходимое упорядочение может быть обеспечено сильным магнитным полем, в котором радиус ларморовских орбит и период циклотронного вращения заряженных частиц много меньше характерных размеров и времён протекающих процессов. Однако такое упорядочение не затрагивает движения заряженных частиц вдоль силовых линий магнитного поля, так что давление такой слабостолкновительной плазмы обычно анизотропно, и для замыкания (или обрыва) цепочки моментных уравнений требуются дополнит. предположения. (Напр., в гидродинамике Чу – Гольдбергера – Лоу для замыкания уравнений пренебрегают потоками тепла вдоль магнитного поля.)
Изменяется и условие вмороженности: магнитное поле может «проскальзывать» по отношению к движению массы плазмы. Иногда допустимо говорить о вмороженности магнитного поля в наиболее лёгкую и подвижную компоненту – в электроны. Двухжидкостную модель квазинейтральной плазмы с магнитным полем, вмороженным в электронную жидкость, иногда называют холловской М. г. Эта разновидность МГД-теории более адекватна для описания течений плазмы с сильно неоднородным током. Другой предельный случай квазинейтрального движения на сравнительно коротких временны́х промежутках, когда можно пренебречь движением тяжёлых ионов по сравнению с движением более подвижных электронов, называют электронной М. г. В астрофизич. приложениях используют обобщения МГД-теории на случай релятивистских скоростей, ковариантную форму записи, пригодную для задач общей теории относительности, и др.
Успехи МГД-теории объясняются наглядностью её проявлений в макроскопич. физич. явлениях и практич. использованием её предсказаний. Совр. развитие М. г. связано с исследованием свойств и моделированием сложных систем, а также с расширением области применения МГД-теории, в т. ч. путём включения в М. г. кинетич. эффектов.
-
Рис. 1. При течении электропроводящей жидкости поперёк магнитного поля со скоростью v в ней возникает электрическое поле E, ортогональное к направлениям потока и магнитного поля B. -
Рис. 2. Пример поля скоростей в развитой магнитогидродинамической турбулентности. Рассчитаны линии потока плазмы в поперечном сечении магнитной ловушки; видны крупномасштабные структуры (вихри) на фоне мелкомасштабных осцилляций.
