ПЕРЕСОЕДИНЕ́НИЕ МАГНИ́ТНЫХ СИЛОВЫ́Х ЛИ́НИЙ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ПЕРЕСОЕДИНЕ́НИЕ МАГНИ́ТНЫХ СИЛОВЫ́Х ЛИ́НИЙ в плазме, изменение топологии силовых линий магнитного поля, связанное с нарушением их вмороженности в плазму; обычно сопровождается высвобождением свободной магнитной энергии, накопленной в разл. плазменных конфигурациях, и её преобразованием в тепловую и кинетич. энергию частиц, которые могут ускоряться вплоть до ультрарелятивистских скоростей. При П. м. с. л. возникают новые магнитные структуры: магнитные петли, острова, нейтральные точки и линии, новые течения плазмы.
Нарушение свойственной идеальной магнитной гидродинамике вмороженности магнитного поля в плазму обусловливает разл. механизмы П. м. с. л.: резистивный (вызванный конечной электрич. проводимостью плазмы $σ$), инерционный (обусловленный конечной массой носителей заряда – электронов), а также связанные с эффектом Холла, вязкостью и анизотропией давления электронной компоненты плазмы. Кинетич. теория позволяет учесть механизм пересоединения, связанный с бесстолкновительным резонансным Ландау затуханием. П. м. с. л. возможно и при наличии аномального сопротивления, возникающего при рассеянии электронов на разл. плазменных микронеустойчивостях. Различают вынужденное и спонтанное (происходящее без внешнего воздействия) пересоединение магнитных силовых линий.
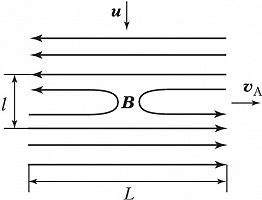
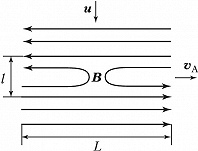
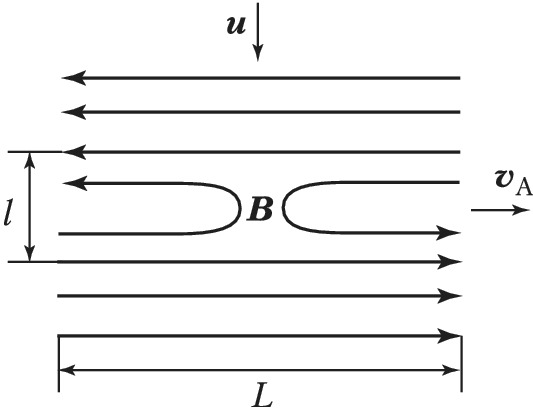
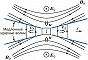
В наиболее известных моделях вынужденного пересоединения (модели Паркера – Свита, Петчека и Сыроватского) изучаются течения плазмы под действием внешнего электрич. поля напряжённостью $\boldsymbol{E}_0$. В этих моделях магнитные поля индукцией $\boldsymbol{B}_0$ на границах системы направлены антипараллельно, поэтому в центр. части системы существует особая нейтральная линия, где магнитное поле обращается в нуль. Скорость П. м. с. л. определяется граничными условиями, т. е. способом организации течения плазмы к области пересоединения, и числом Маха $M=u/v_A$, где $u=cE_0/B_0$ – скорость плазменного потока, $v_A=B_0/(4πnmi)^{1/2}$ – альвеновская скорость, $n$ – концентрация ионов плазмы с массой $m_i$, $c$ – скорость света. Согласно модели Паркера – Свита (рис. 1), процесс диссипации магнитного поля осуществляется лишь в малой диффузионной области размером $l=L/Re_m^{1/2}$ (здесь $Re_m=4πσv_A L/c^2≫1$ – магнитное число Рейнольдса, $L$ – характерная ширина слоя), где аннигилирует небольшое количество магнитного потока. В этом случае скорость пересоединения (отношение скорости втекающего потока к альвеновской скорости) равна $M=Re_m^{1/2}$.
Модель Паркера – Свита хорошо описывает процессы медленного П. м. с. л. в столкновительной плазме.
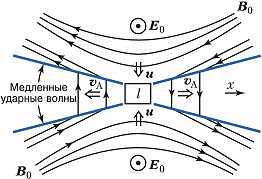
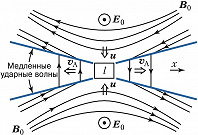
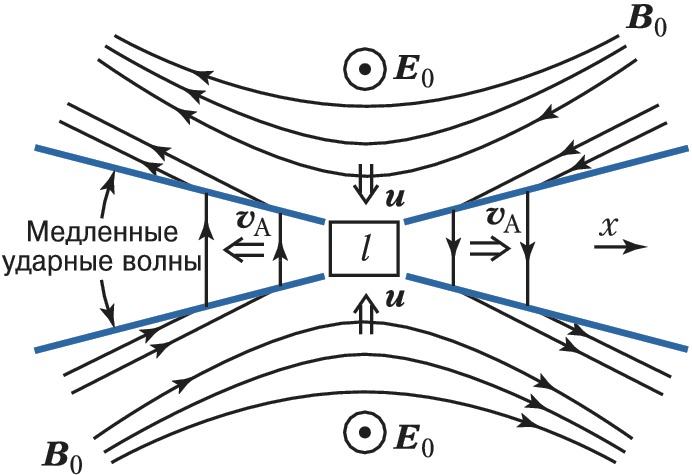
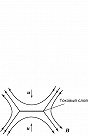
В модели Петчека (рис. 2) под действием скрещенных электрич. $\boldsymbol{E}_0$ и магнитного $\boldsymbol{B}_0$ полей плазма вместе с вмороженными магнитными силовыми линиями дрейфует со скоростью $\boldsymbol{u}$ к нейтральной линии, перпендикулярной плоскости рисунка. Вокруг диффузионной области, где происходит разрыв и пересоединение силовых линий, расположены четыре стоячие ударные волны, пересекая которые потоки плазмы направляются направо или налево от области пересоединения. Ударные волны изгибают магнитные силовые линии; в итоге скорость пересоединения увеличивается до величины $M∼1/\ln Re_m$.
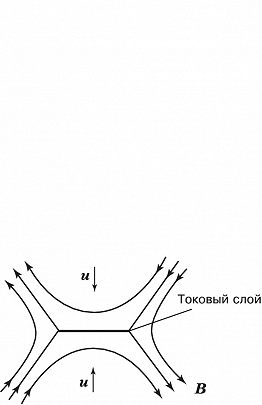
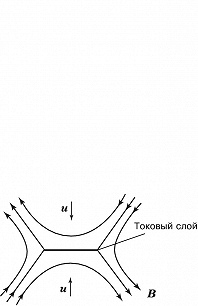
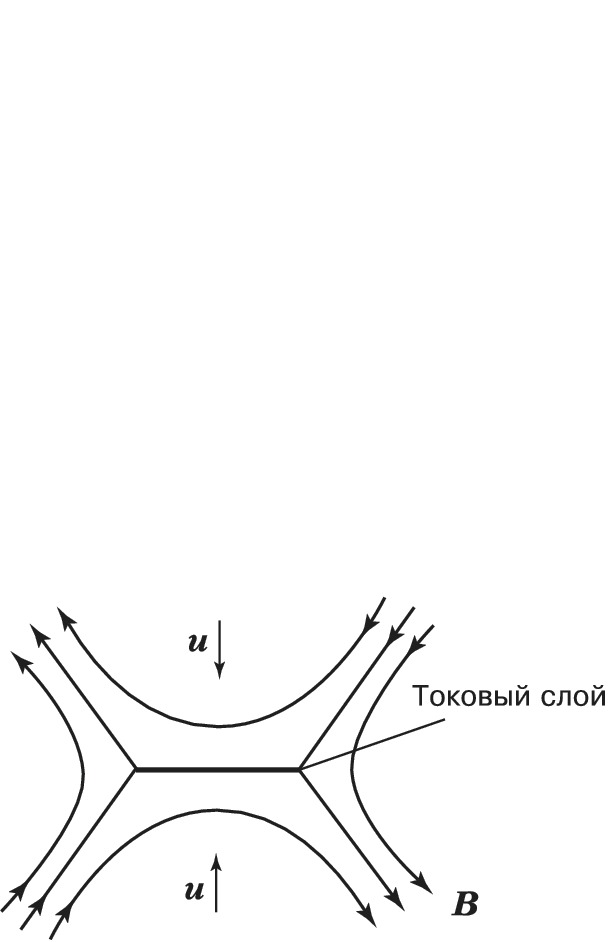
В модели разрыва нейтрального токового слоя Сыроватского процесс П. м. с. л. рассматривается как динамический и нестационарный (рис. 3). Исходная конфигурация магнитных полей схожа с конфигурацией модели Петчека, но в ней под действием электрич. поля реализуется течение не квазистационарного, а кумулятивного типа. Поток вмороженного в плазму магнитного поля, поступающий к нейтральной линии со скоростью $\boldsymbol{u}$, не успевает пересоединиться и «уплотняется» в окрестности удлиняющегося в обе стороны токового слоя, где плотность частиц быстро убывает, что приводит к разрыву слоя. Возникают сильные импульсные индукционные электрич. поля, которые могут ускорять частицы плазмы до больших скоростей. Модель Сыроватского, несмотря на большое количество упрощающих предположений, лучше других согласуется с совр. данными прямых спутниковых измерений в магнитосфере Земли. Подобные динамич. модели вынужденного пересоединения используются при исследовании вспышек на Солнце и в лабораторных экспериментах.
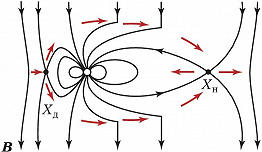
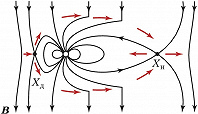
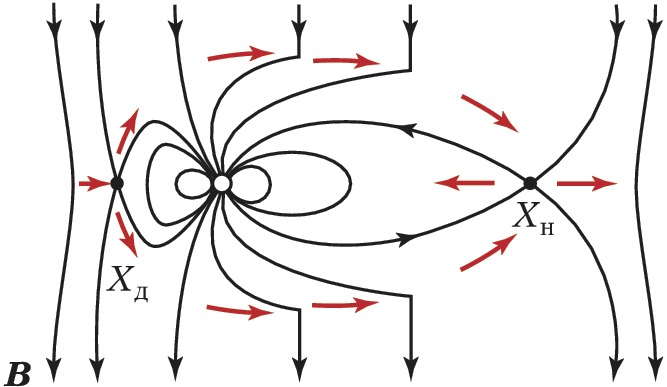
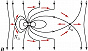
Процесс спонтанного пересоединения впервые исследован в упрощённой модели Харриса нейтрального токового слоя с антипараллельными магнитными полями и нулевой поперечной компонентой. Нарушение вмороженности магнитного поля приводит к пинчеванию поперечного тока и образованию магнитных островов (см. рис. 1 в ст. Нейтральный токовый слой). Спонтанный процесс П. м. с. л. называется разрывной неустойчивостью или тиринг-неустойчивостью. Существуют её резистивные, инерционные и резонансные моды. Для бесстолкновительной космич. плазмы характерна резонансная мода, связанная с затуханием Ландау. Наличие нормальной компоненты магнитного поля кардинально меняет устойчивость системы. В бесстолкновительной плазме разрывная неустойчивость стабилизируется, но магнитная конфигурация метастабильна. В системе накапливается значит. количество магнитной энергии, которая при достижении пороговой величины взрывным образом высвобождается. Эти свойства процессов П. м. с. л. проявляются в солнечных вспышках и магнитосферных суббурях. В космич. плазме процессы П. м. с. л. контролируют структуру и динамику магнитосфер планет. Согласно модели Данжи (рис. 4), межпланетное и геомагнитное поля пересоединяются в лобовой области на границе магнитосферы Земли, образуя гигантские магнитные «трубки» диаметром порядка 1–2 радиусов Земли. Эти магнитные «трубки» с потоком солнечной плазмы, обтекающей магнитосферу, уносятся на ночную сторону Земли и там снова пересоединяются в обратной последовательности.
-
Рис. 1. Модель пересоединения Паркера – Свита. -
Рис. 2. Модель вынужденного пересоединения Петчека. Пересоединение силовых линий осуществляется в малой диффузионной области l. Синими линиями показаны ударные магнитогидродинамические волны, на которых происходит основное торможение плазменного потока. -
Рис. 3. Модель токового слоя Сыроватского. -
Рис. 4. Модель пересоединения магнитных силовых линий Данжи. Xд и Xн – нейтральные области,где происходит пересоединение. Красными стрелками показано направление движения плазмы при обтекании магнитосферы солнечным ветром.
