ИНТЕРФЕРО́МЕТР
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ИНТЕРФЕРО́МЕТР, прибор, действие которого основано на явлении интерференции волн. В соответствии с природой волн существуют атомный И. (см. Атомная оптика), интерферометр акустический и И. для электромагнитных волн. К последним относятся оптический И. и радиоинтерферометр (см. Апертурный синтез). Ниже рассмотрены оптич. И., которые получили наибольшее распространение как приборы для измерения длин волн спектральных линий и их структуры; для измерения показателей преломления прозрачных сред; в метрологии для абсолютных и относит. измерений длин и перемещений тел; для измерения угловых размеров звёзд (звёздный интерферометр); для контроля формы, микрорельефа и деформации поверхностей оптич. деталей и пр.
Применение И. в одночастотных лазерах позволило существенно улучшить и автоматизировать технику интерферометрич. измерений, повысить точность измерения. В лазерных И. производится фотоэлектрич. регистрация разности хода, выраженной непосредственно в длинах волн. Созданы голографич. И. (см. Голографическая интерферометрия), позволяющие регистрировать небольшие изменения формы поверхности или предмета, возникающие в результате тех или иных деформаций.
В основе работы И. лежит пространственное разделение пучка света с помощью к.-л. устройства для получения двух или более взаимно когерентных лучей, которые проходят разл. оптич. пути, а затем сводятся вместе, и наблюдается результат их интерференции. Вид интерференционной картины зависит от способа разделения пучка света на взаимно когерентные лучи, от их числа, их относит. интенсивности, размеров источника, спектрального состава света.
Многолучевые И. используются гл. обр. как спектрометры высокого разрешения для исследования тонкой структуры спектральных линий (см. Спектральные приборы), а двухлучевые И. являются в осн. технич. приборами.
Двухлучевые интерферометры
Если один луч проходит геометрич. путь $l_1$ в среде с показателем преломления $n_1$, а другой – путь $l_2$ в среде с $n_2$, то оптич. разность хода лучей $Δ=l_1n_1-l_2n_2+δ$ определяет результат интерференции. Здесь $δ$ – изменение фазы на границах раздела сред. Интенсивность света в данной точке образующейся интерференционной картины при равных амплитудах $A$ интерферирующих лучей и $l_1=l_2=l$ определяется выражением: $I=4A^2\cos^2(πΔ/l)$. При $Δ=mλ$ ($m=0,\, ±1,\, ±2,…$ – порядок интерференции) интенсивность имеет макс. значение – максимум интерференционной полосы. Различным $m$ соответствуют полосы разного порядка. Изменение любой из величин $l,\, n$ или $λ$ приводит к смещению интерференционных полос. Измеряя величину смещения полос при постоянных $l$ и $λ$ , определяют изменение $n$, напр., интерференционными рефрактометрами Рэлея или Жамена. Если известны $λ$ и $n$, то по смещению полос можно измерить геометрич. длины, для чего служат интерференционные компараторы. Так как интерференционная картина смещается заметно даже при небольших (порядка $0,1λ$) изменениях разности хода $Δ$, точность измерения с помощью И. очень высока (поскольку $λ≈0,5$ мкм).
При использовании источника монохроматич. света в поле зрения И. наблюдается большое число светлых и тёмных интерференционных полос разл. порядков. Если в И. используют источник белого света (напр., лампу накаливания), то в поле зрения наблюдается лишь небольшое число (8–10) цветных полос низкого порядка.
Методы, с помощью которых в И. могут быть получены когерентные пучки, весьма разнообразны, и потому существует большое число разл. конструкций И., обычно приспособленных к измерению к.-л. одной величины ($l,\, n$ или $λ$). По методу получения когерентных пучков И. делятся на два типа. В одном из них когерентные пучки получаются в результате отражения от двух поверхностей плоскопараллельной или клиновидной пластинки. В И. др. типа происходит интерференция лучей, вышедших из источника под углом друг к другу (см. Интерференция света). К первому типу относятся И. Жамена, Физо, Майкельсона и др., ко второму – И. Рэлея и др.
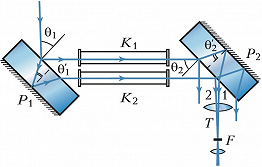
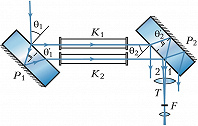
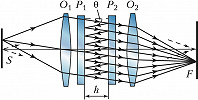
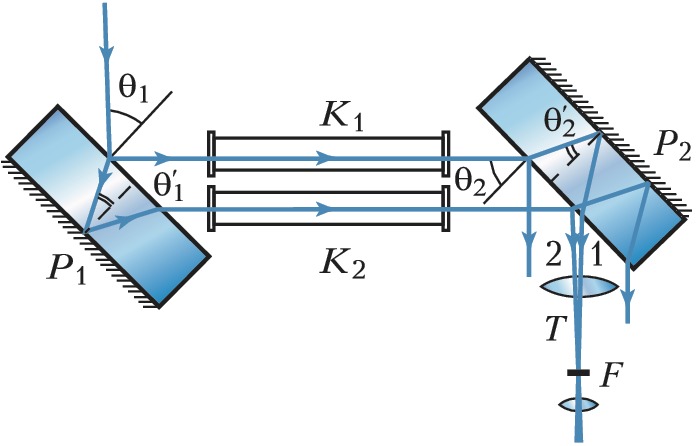
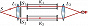
Интерферометр Жамена, предназначенный для измерения показателей преломления жидкостей и газов, состоит из двух одинаковых толстых стеклянных пластин $P_1$ и $P_2$ (рис. 1). Задние поверхности пластин посеребрены. Пучок света от источника падает под углом, близким к 45°, на пластину $P_1$. В результате отражения от передней и задней поверхностей пластины $P_1$ возникают два параллельных пучка, каждый из которых, в свою очередь, раздваивается при отражении от двух поверхностей пластины $P_2$. Средние пучки 1 и 2 при наложении друг на друга образуют интерференционную картину в фокальной плоскости зрительной трубы $T$. Разность хода между ними $Δ=2nh(\cos θ'_2 - \cos θ'_1)$, где h – толщина пластин из материала с показателем преломления $n,\, θ_1$ и $θ_2$ – углы падения на поверхности пластин $P_1$ и $P_2$; и – соответствующие углы преломления. Если пластины строго параллельны, то $θ'_1=θ'_2$ и $Δ=0$; поле зрения будет равномерно освещённым. При юстировке одну из пластин слегка наклоняют и в установленной на бесконечность зрительной трубе видны эквидистантные интерференционные полосы. Если теперь на пути интерферирующих пучков поместить кюветы $K_1$ и $K_2$ с веществами с известным $n_1$ и неизвестным $n_2$ показателями преломления, то оптич. разность хода изменится и интерференционная картина сместится на $Δ= (n_2-n_1)l$ ($l$ – длина кюветы). Это позволяет определить $n_2$.
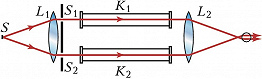
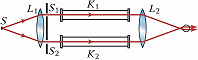
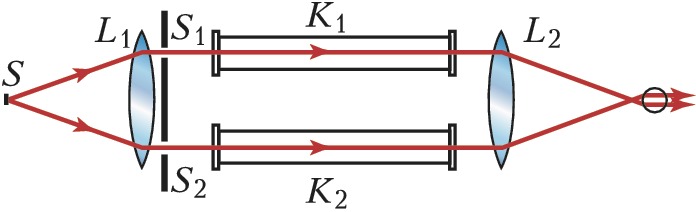
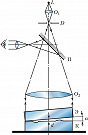
Интерферометр Рэлея тоже позволяет определить показатель преломления. Источник света $S$ (рис. 2) располагается в фокальной плоскости линзы $L_1$. Выходящий из неё параллельный световой пучок поступает на диафрагму с отверстиями $S_1$ и $S_2$. Пучки света от $S_1$ и $S_2$ проходят через кюветы $K_1$ и $K_2$ и образуют интерференционные полосы в фокальной плоскости линзы $L_2$. Как и в случае И. Жамена, при прохождении света через кюветы появляется добавочная разность хода $Δ$ и по смещению полос определяют неизвестный показатель преломления.
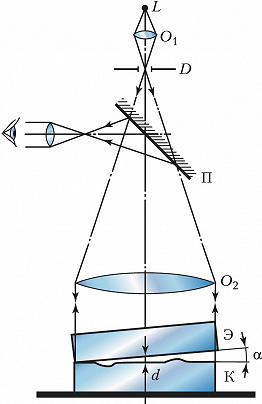
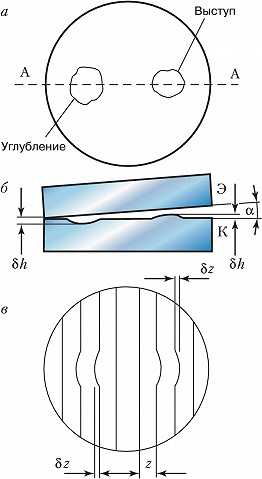
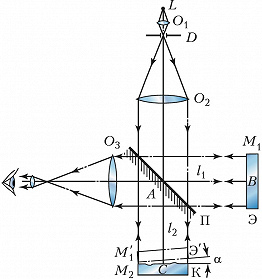
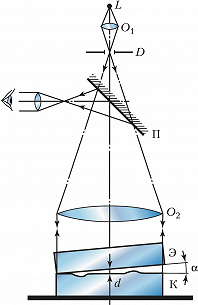
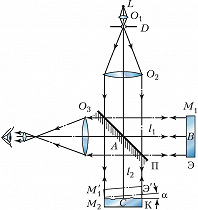
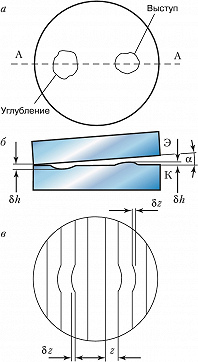
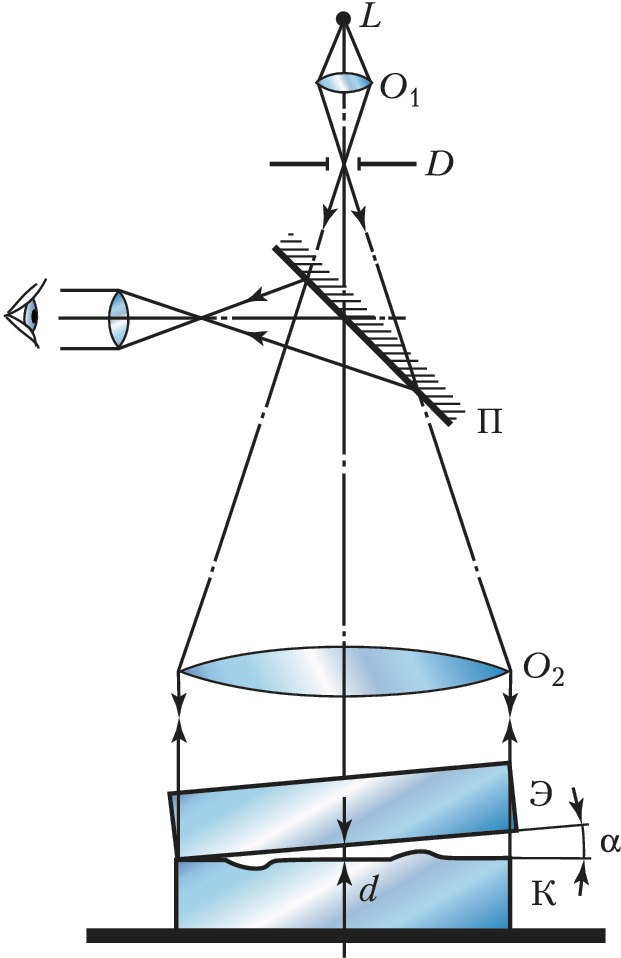
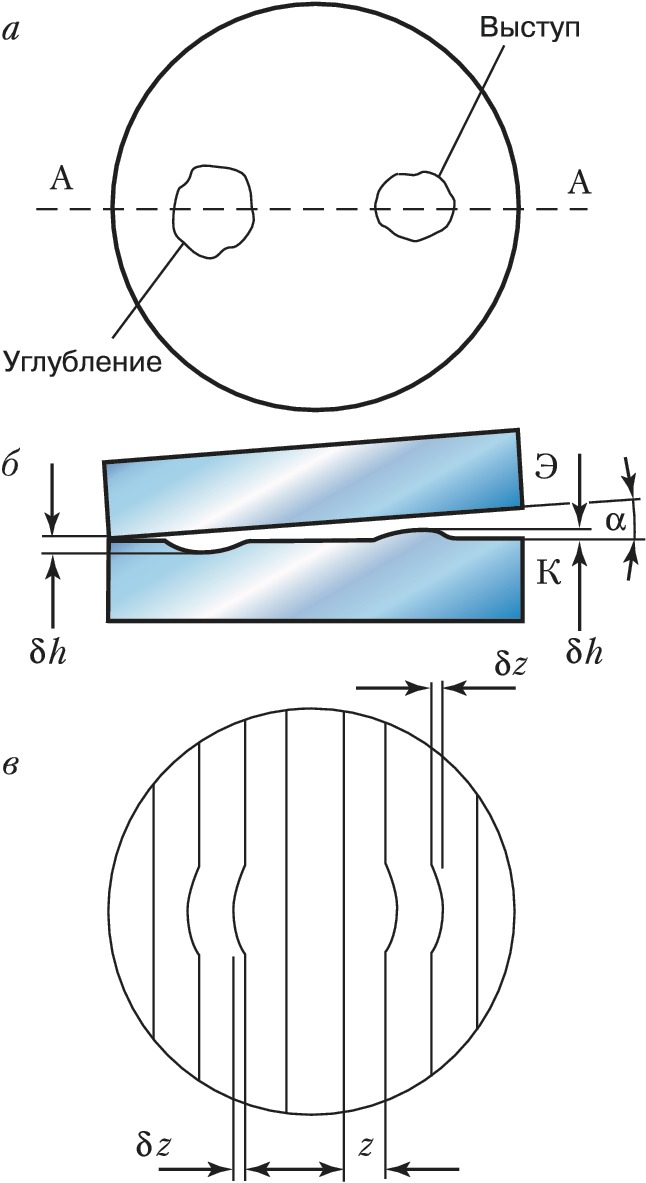
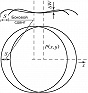
Контроль точности изготовления плоских поверхностей оптич. деталей осуществляют с помощью интерферометра Физо (рис. 3). Свет от монохроматич. источника $L$ с помощью конденсора $O_1$, диафрагмы $D$ и объектива $O_2$ направляется параллельным пучком на эталонную Э и контролируемую К пластинки (положенные одна на другую и образующие между собой небольшой угол $α$ ) почти перпендикулярно их поверхностям. С помощью полупрозрачной пластинки П в отражённом свете наблюдаются интерференционные полосы равной толщины. Положения этих полос определяются из условия: $Δ= 2dn+λ /2=mλ= \text{const}$, где $d$ – толщина воздушного клина. Если контролируемая поверхность идеально плоская, то наблюдаются полосы равного наклона, имеющие форму прямых эквидистантных линий, параллельных ребру клина $(d=\text{const})$, расстояние между которыми равно $z=λ /2α$ (при $α= 10″$ и $λ≈0,5$ мкм, $z=5$ мм). Если же на контролируемой поверхности имеются к.-л. дефекты, напр. небольшие углубления или выступы (рис. 4, а,б), или она не строго плоская, то в области расположения этих дефектов наблюдаются отклонения $δz$ от прямолинейности (рис. 4,в). При этом относит. величина отклонения $δz/z$ связана с высотой или глубиной дефекта $δh$ соотношением $δh=(δ/2)δz/z$. Невооружённый глаз может оценить величину $δz/z≈ 0,l$, что соответствует величине обнаруженного дефекта $δh=λ/20$ (при $λ= 0,633$ мкм, $δh= 0,031$ мкм). Знак отклонения позволяет отличить тип дефекта: углубление или выступ (рис. 4,в). Если контролируемая поверхность имеет форму сферы, то интерференционные полосы имеют форму концентрич. окружностей (см. Ньютона кольца).
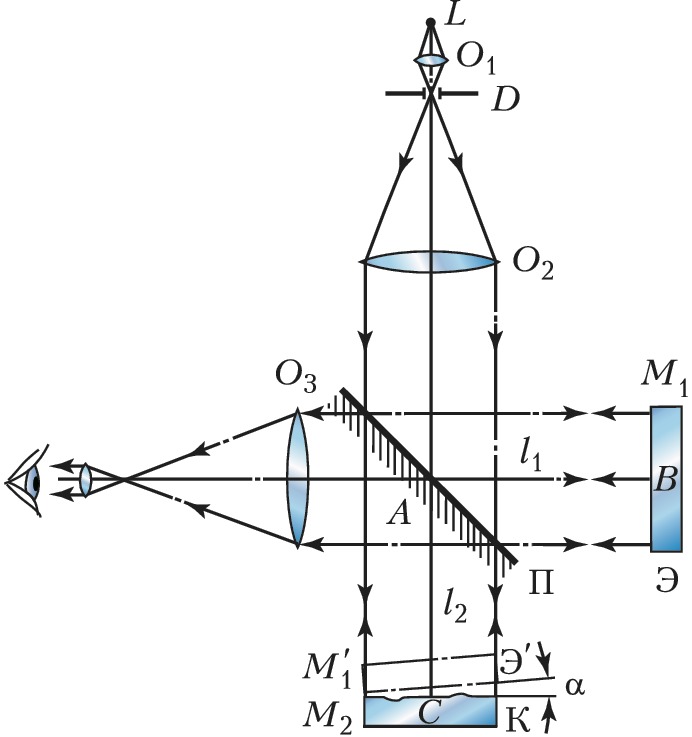
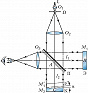
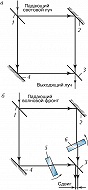
Поверхности контролируемой и эталонной пластинок в И. Физо из-за малости угла (порядка угловых секунд) почти полностью соприкасаются друг с другом и в процессе юстировки могут быть повреждены. Поэтому для контроля поверхностей часто используются бесконтактные И., построенные по схеме интерферометра Майкельсона (рис. 5). Здесь параллельный пучок света из объектива $O_2$ входного коллиматора падает на полупрозрачную разделит. пластинку П и направляется к зеркалам $M_1$ и $M_2$, которыми в данном случае служат эталонная Э и контролируемая К пластинки. После отражения от зеркал-пластинок оба пучка вновь соединяются разделит. пластинкой П, направляются в объектив $O_3$ выходного коллиматора и интерферируют. При этом оба зеркала ориентированы так, чтобы контролируемая поверхность К и мнимое изображение Э′ эталонной поверхности Э в разделит. пластинке образовали небольшой воздушный клин толщиной в его ср. части (на оптич. оси) $d=l_2-l_1$, где $l_1$ и $l_2$ – расстояния от разделит. пластинки до зеркал, $l_1=AB,\, l_2=AC$. При интерференции наблюдаются полосы равной толщины, локализованные в плоскости клина, максимумы интенсивности которых определяются из условия $$Δ=2(l_2–l_1)=2d=mλ.$$ Анализ интерференционной картины проводится так же, как и в И. Физо. Модернизованный И. Майкельсона, в котором одно из плоских зеркал заменено сферическим, позволяет проводить контроль качества сферич. (выпуклых или вогнутых) зеркал и качества объективов. Принцип И. Майкельсона широко используется в ряде др. технич. И., напр. в И. для измерения абсолютных и относит. длин концевых мер. Большое число лазерных И. также построено по схеме И. Майкельсона. Благодаря высокой монохроматичности и когерентности лазерного излучения такие И. позволяют проводить измерения при больших разностях хода, напр. измерять с высокой точностью большие линейные перемещения тел (достигающие нескольких метров), проводить проверку штриховых эталонных мер, шкал и др.
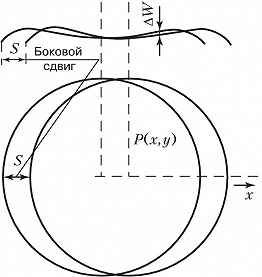
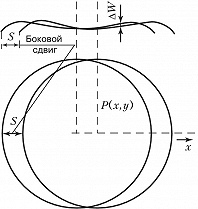
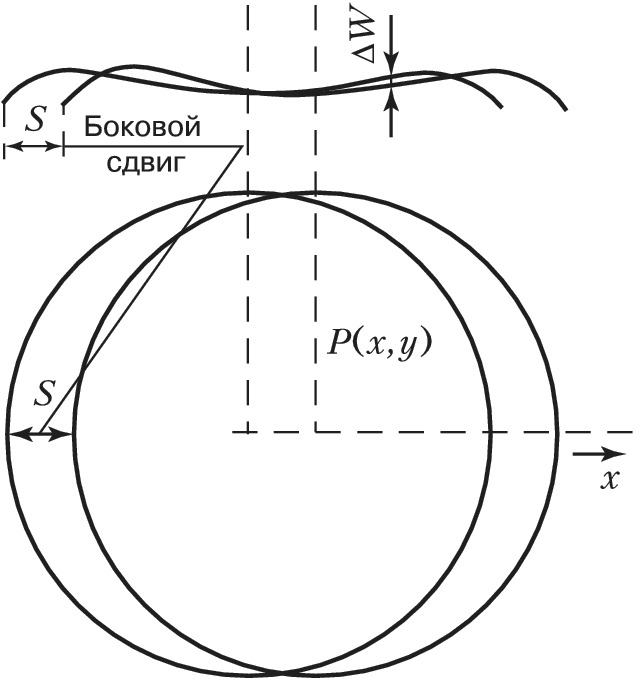
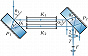
В некоторых случаях двухлучевые И. используются в качестве сдвиговых интерферометров, позволяющих получить информацию об искажении волнового фронта светового пучка. Эта информация, в свою очередь, даёт возможность определить характеристики среды и оптич. элементов, через которые проходит пучок. Наибольшее распространение получили И. поперечного сдвига. Для пояснения принципа их работы считают, что исследуемый волновой фронт является почти плоским, с небольшими отклонениями $W(x,y)$ (рис. 6) от плоскости ($x,y$ – координаты произвольной точки $P$). При смещении фронта на величину $S$ в направлении $x$ его погрешность в точке $P$ составит $W(x-S,y)$, а результирующая разность хода $ΔW$ для двух фронтов определится как $W(x,y) -W(x-S,y)$. Разность хода в разл. точках волнового фронта ΔW=mλΔW=mλ, где $m$ – порядок интерференционной полосы. И. поперечного сдвига даёт информацию об отклонении луча в угловых единицах.
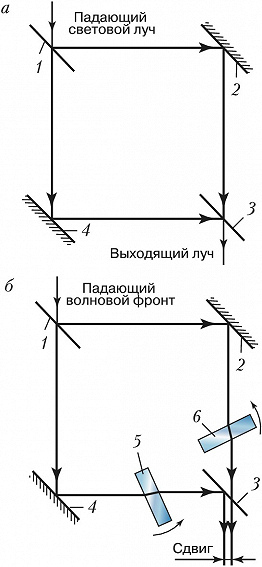
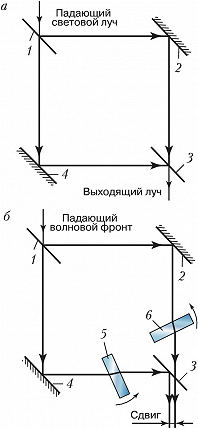
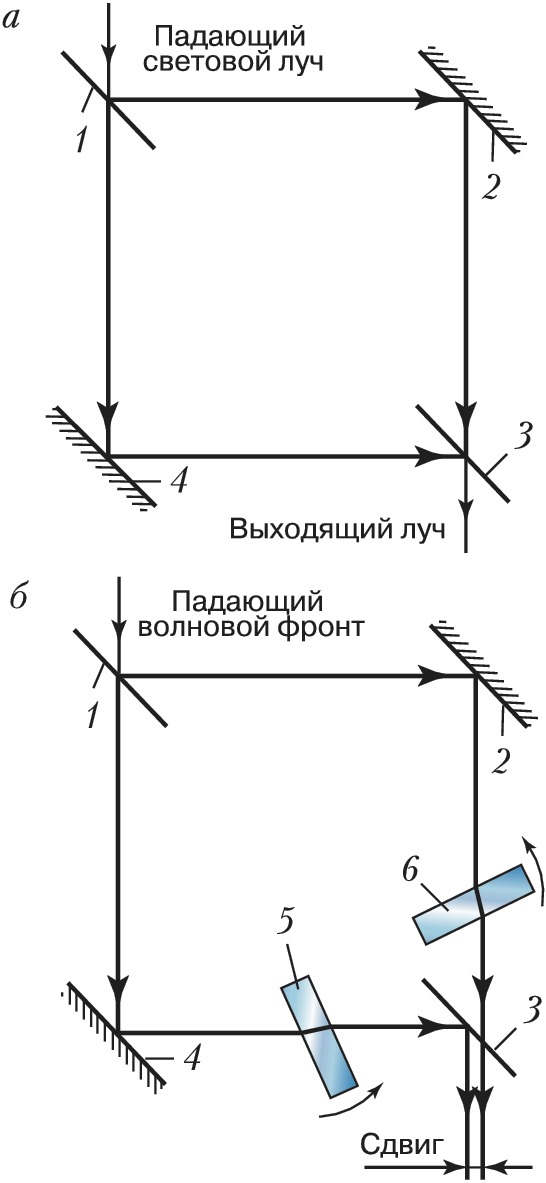
Для работы в сдвиговом режиме можно использовать интерферометр Маха – Цендера, состоящий обычно из двух светоделителей (1, 3) и двух плоских зеркал (2, 4) (рис. 7, а). Для этого в плечи И. вводят плоскопараллельные пластины (5, 6), изготовленные из одного материала и имеющие одинаковую толщину (рис. 7, б). Меняя наклон плоскопараллельных пластин, можно менять величину поперечного сдвига пучков на выходе интерферометра.
Многолучевые интерферометры
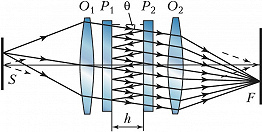
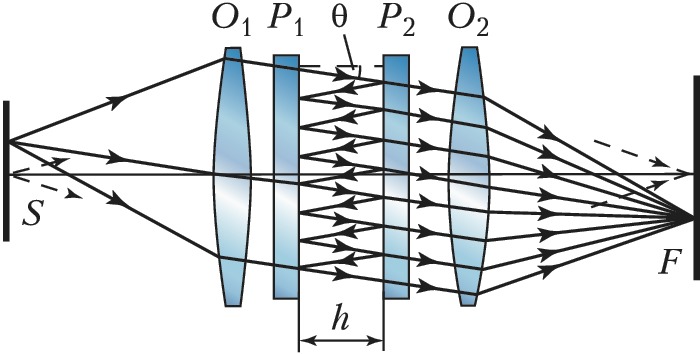
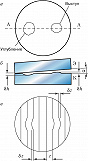
Самым известным многолучевым И. является интерферометр Фабри – Перо (рис. 8), состоящий из двух стеклянных или кварцевых параллельных пластин $P_1$ и $P_2$, расположенных на расстоянии $h$ друг от друга, на внутр. поверхности которых нанесены зеркальные покрытия с высоким (0,85–0,98) коэф. отражения. Параллельный пучок света, падающий из объектива $O_1$, в результате многократного отражения от зеркал образует большое число параллельных когерентных пучков с постоянной разностью хода $Δ=2nh\cos q$ между соседними пучками, но разл. интенсивности. В результате многолучевой интерференции в фокальной плоскости $F$ объектива $O_2$ образуется интерференционная картина в форме концентрич. колец с резкими максимумами интенсивности, положение которых определяется из условия $Δ_{\text{макс}}=mλ$ ($m$ – целое число), т. е. зависит от длины волны. Поэтому И. Фабри – Перо разлагает сложное излучение в спектр и применяется как интерференционный спектральный прибор высокой разрешающей силы, зависящей от коэф. отражения зеркал $ρ$ и от $h$, возрастая с их увеличением. Так, при $ρ= 0,9$, $h=100$ мм, $λ=500$ нм миним. разрешаемый интервал длин волн $δλ=5·10^{-3}$ нм. Для исследования спектров в видимой, ИК и сантиметровой областях длин волн используются спец. сканирующие устройства с фотоэлектрич. регистрацией.
Кроме И., основанных на стационарной интерференции, существуют И. на базе лазерных устройств, использующие нестационарную интерференционную картину. Так, для измерения небольших перемещений и длин деталей применяется И., действие которого основано на зависимости разностной частоты излучения между соседними продольными модами лазера $f=c/2L$ от длины резонатора $L$ ($c$ – скорость света). По изменению разностной частоты $Δf$, происходящему при перемещении одного из зеркал резонатора, измеряют величину этого перемещения $ΔL=2L^2Δf/c$. Преимуществом таких И. является то, что измерение линейных размеров (и перемещений) сводится к определению частоты, которую можно измерить радиотехнич. методами с высокой степенью точности.
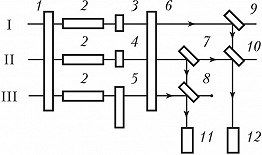
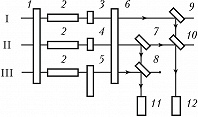
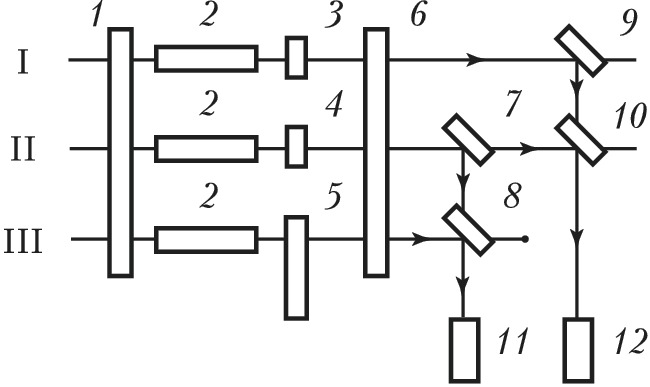
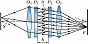
Многолучевые лазерные интерферометры основаны на регистрации нестационарной интерференции парциальных световых пучков. На рис. 9 приведена схема трёхлучевого лазерного И., выполняющего функцию акселерометра. И. представляет собой резонатор, образованный протяжёнными зеркалами 1 и 6, в котором размещены три активных элемента 2, определяющие независимую генерацию по трём параллельным каналам I, II, III. В каналах I и III, играющих роль сигнальных, установлены чувствит. элементы 3 и 5, меняющие показатель преломления под действием ускорения. В канале II установлен опорный элемент 4, не реагирующий на ускорение и играющий роль компенсатора, что позволяет получить равные (или близкие) частоты генерации во всех трёх каналах при отсутствии ускорений. Чувствит. элементы обычно выполняются в виде прямоугольных сосудов, заполненных газом. Воздействие ускорения на оптич. систему приводит к появлению градиента давления газа, что вызывает изменение показателя преломления в сигнальных каналах и, следовательно, изменение частоты генерации. Большая сторона параллелепипеда параллельна измерительной оси ($x$ или $y$). Ортогональная ориентация измерительных осей в каналах I и III позволяет реализовать акселерометр, реагирующий на две составляющие $a_x$ и $a_y$ произвольного вектора ускорения. Для измерения изменений частот генераций в сигнальных каналах генерируемое в них излучение смешивается с помощью системы светоделителей (7–10) с излучением опорного канала и подаётся на фотоприёмники 11, 12, регистрирующие световые биения на разностных частотах. По величине разностных частот определяются изменения показателя преломления в сигнальных каналах и выявляются составляющие ускорения $a_x$ и $a_y$.
Все рассмотренные выше И. относятся к классу амплитудных. В них сначала формируется интерференционная картина, а затем регистрируется распределение интенсивности (в пространстве или во времени) для определения изменений в структуре интерференции, происходящих в процессе измерений.
Наряду с амплитудными И. для определения характеристик когерентности световых пучков используются также интерферометры интенсивности. В них интерференционная картина не наблюдается, а необходимую информацию получают, измеряя корреляцию интенсивностей, регистрируемых двумя пространственно разнесёнными приёмниками излучения.
-
Рис. 9. Схема трёхлучевого лазерного интерферометра. -
Рис. 2. Схема интерферометра Рэлея. -
Рис. 3. Схема интерферометра Физо (для наглядности угол α и размеры дефектов увеличены). -
Рис. 1. Схема интерферометра Жамена. -
Рис. 5 Схема интерферометра Майкельсона для контроля плоских поверхностей бесконтактным методом. -
Рис. 6. Схематическое изображение (план и боковая проекция) исходного и сдвинутого волновых фронтов с круглой апертурой. Интерференционные полосы возникают в их общей перекрывающейся области. -
Рис. 7. Интерферометр Маха – Цендера: а – обычная схема; б – схема для работы в сдвиговом режиме; 1, 3 – светоделители, 2, 4 – плоские зеркала, 5, 6 – вращаемые плоскопараллельные пластины. -
Рис. 8. Схема интерферометра Фабри – Перо. -
Рис. 4. а – Вид дефектов сверху на контролируемой пластинке; б – сечение эталонной и контрольной пластинок по линии А – А (угол α и размеры дефектов для наглядности сильно увеличены); в – вид интерференционной картины (полосы равной толщины) в интерферометре Физо.
