НЬЮ́ТОНА КО́ЛЬЦА

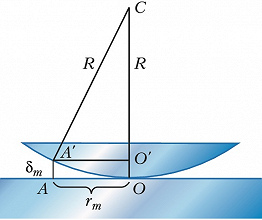
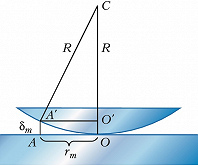
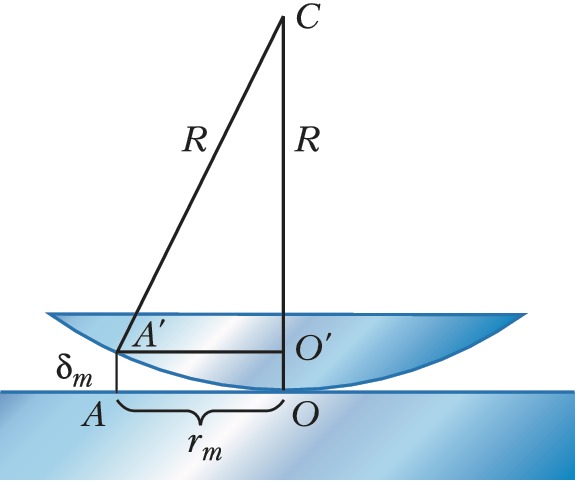
НЬЮ́ТОНА КО́ЛЬЦА, ин­тер­фе­рен­ци­он­ные по­ло­сы рав­ной тол­щи­ны

в фор­ме кон­цен­три­че­ских ко­лец, рас­по­ло­жен­ных во­круг точ­ки ка­са­ния двух сфе­рич. по­верх­но­стей ли­бо плос­ко­сти и сфе­ры. Впер­вые опи­са­ны в 1675 И. Нью­то­ном

 >>

. Ин­тер­фе­рен­ция све­та про­ис­хо­дит в тон­ком за­зо­ре (обыч­но воз­душ­ном), раз­де­ляю­щем со­при­ка­саю­щие­ся по­верх­но­сти; этот за­зор иг­ра­ет роль тон­кой плён­ки (см. Оп­ти­ка тон­ких сло­ёв

 >>

). Н. к. на­блю­да­ют­ся и в про­хо­дя­щем, и (бо­лее от­чёт­ли­во) в от­ра­жён­ном све­те. При ос­ве­ще­нии мо­но­хро­ма­тич. све­том дли­ны вол­ны $λ$ Н. к. пред­став­ля­ют со­бой че­ре­дую­щие­ся тём­ные и свет­лые коль­ца. Свет­лые коль­ца воз­ни­ка­ют в мес­тах, где раз­ность фаз ме­ж­ду пря­мым и два­ж­ды от­ра­жён­ным лу­чами (в про­хо­дя­щем све­те) или ме­ж­ду лу­ча­ми, от­ра­жён­ны­ми от обе­их со­при­ка­саю­щих­ся по­верх­но­стей (в от­ра­жён­ном све­те), рав­на $2 \pi n \ (n=1, 2, 3, ...$) (т. е. раз­ность хо­да лу­чей $Δ_m$ рав­на чёт­но­му чис­лу по­лу­волн). Тём­ные коль­ца об­разу­ют­ся там, где раз­ность фаз рав­на $(2n+1)\pi$. Раз­ность фаз лу­чей оп­ре­де­ля­ет­ся тол­щи­ной за­зо­ра $\delta_m$ с учё­том из­ме­не­ния фа­зы све­то­вой вол­ны при от­ра­же­нии (см. От­ра­же­ние све­та

 >>

). Так, при от­ра­же­нии от гра­ни­цы воз­дух–стек­ло фа­за ме­ня­ет­ся на π, а при от­ра­же­нии от гра­ни­цы стек­ло–воз­дух фа­за ос­та­ёт­ся не­из­мен­ной. По­это­му в слу­чае двух стек­лян­ных по­верх­но­стей (рис.), с учё­том раз­ли­чий в ус­ло­ви­ях от­ра­же­ния от ниж­ней и верх­ней по­верх­но­стей за­зо­ра (по­те­ря по­лу­вол­ны), $m$-е тём­ное коль­цо об­ра­зу­ет­ся, ес­ли $Δ_m=2\delta_m+\lambda/2=(2m+1)\lambda/2$, т. е. при тол­щи­не за­зо­ра $\delta_m=m\lambda/2$. Ра­ди­ус $r_m m$-го коль­ца оп­ре­де­ля­ет­ся из треуголь­ни­ка $A' O'C'$: $r_m^2=R^2-(R-\delta_m)^2$≈$2R\delta_m$, от­ку­да $r_m=\sqrt{2R\delta_m}$, а для тёмного $m$-го коль­ца $r_m=\sqrt{Rm \lambda}$. Это со­отношение по­зво­ля­ет с хо­ро­шей точ­но­стью оп­ре­де­лять $\lambda$ по из­ме­ре­ни­ям $r^m$. Ес­ли $\lambda$ из­вест­на, Н. к. мож­но ис­поль­зо­вать для из­ме­ре­ния ра­диу­сов по­верх­но­стей линз и кон­тро­ля пра­виль­но­сти фор­мы сфе­рич. и пло­ских по­верх­но­стей. При ос­ве­ще­нии не­мо­но­хро­ма­тическим (напр., бе­лым) све­том Н. к. ста­но­вят­ся цвет­ны­ми. Наи­бо­лее от­чёт­ли­во Н. к. на­блю­да­ют­ся при ма­лой тол­щи­не за­зо­ра (т. е. при ис­поль­зо­ва­нии сфе­рич. по­верх­но­стей боль­ших ра­диу­сов).