КОМБИНАТО́РНЫЕ ЗАДА́ЧИ КЛАССИ́ЧЕСКИЕ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
КОМБИНАТО́РНЫЕ ЗАДА́ЧИ КЛАССИ́ЧЕСКИЕ, задачи выбора и расположения элементов конечного множества, в которых на выбор и расположение налагаются те или иные условия. К К. з. к. можно отнести мн. задачи развлекательного характера типа головоломок.
Одной из К. з. к., упоминающейся ещё в мифах Древнего Востока, является построение магич. квадратов, т. е. расположение первых $n^2 $ натуральных чисел в квадрате $n×n$ так, чтобы все суммы чисел по строкам, столбцам и диагоналям были равны одному и тому же числу. Напр., $$\begin{matrix} 4& 9& 2\end{matrix}$$\begin{matrix}3& 5& 7\end{matrix}$$\begin{matrix}8& 1& 6\end{matrix}$$ – магич. квадрат при $n=3$. Известен ряд методов построения таких квадратов. Задача о нахождении формулы для числа магич. квадратов порядка $n$ для любого натурального $n$ до сих пор не решена.
Ряд К. з. к. был рассмотрен Л. Эйлером. Одна из них – задача о 36 офицерах, в которой требуется расположить в ячейках квадрата $6×6 $ (каре) 36 офицеров 6 разл. воинских званий и 6 разл. полков так, чтобы каждая колонна и каждая шеренга содержали одновременно одного и только одного офицера каждого звания и каждого полка. Эта задача эквивалентна задаче о существовании пары ортогональных латинских квадратов порядка 6. Эйлер высказал гипотезу о том, что ортогональных лат. квадратов порядков $n=4k+2, k=1,2,…, $ не существует. В 1900 франц. математик Г. Тарри подтвердил эту гипотезу для $n=6 $ и тем самым доказал, что задача о 36 офицерах не имеет решения. В 1959 инд. математиком С. Човлой, венг. математиком П. Эрдёшем и нем. математиком Г. Штраусом была доказана теорема о существовании пары ортогональных латинских квадратов для каждого $n=4k+2, k=2,3,…$
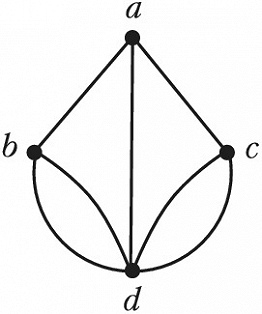
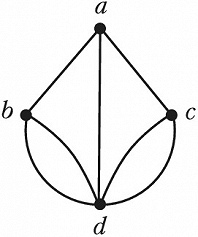
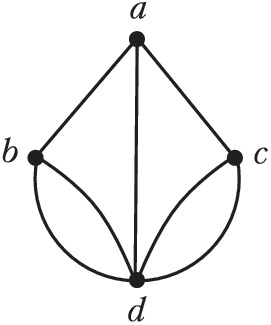
Др. задача, рассмотренная Эйлером, – задача о кёнигсбергских мостах, формулируемая следующим образом. В городе имеется 7 мостов, соединяющих берега реки и 2 острова, расположенные на ней. Спрашивается, можно ли обойти все мосты, проходя по каждому только 1 раз, и возвратиться в исходную точку. В терминах графов теории эта задача формулируется следующим образом. Полагая, что вершины соответствуют районам суши, а рёбра – мостам, задачу о кёнигсбергских мостах можно сформулировать в виде вопроса о возможности последовательного обхода графа, изображённого на рис. 1, проходя его рёбра по одному разу и возвращаясь в исходную точку. Если в графе такой обход возможен, то говорят, что он обладает эйлеровым циклом. Эйлер установил, что такой цикл в графе существует тогда и только тогда, когда он является связным и число рёбер, инцидентных каждой вершине, чётно. Т. к. граф на рис. 1 не удовлетворяет этому требованию, то задача о кёнигсбергских мостах неразрешима. Она неразрешима и в том случае, если отбросить требование совпадения точек начала и конца обхода; в этом случае ставится вопрос о существовании эйлеровой цепи в графе. Граф обладает эйлеровой цепью тогда и только тогда, когда он связен и число вершин, инцидентных нечётному числу рёбер, равно 0 или 2. Граф на рис. 1 не удовлетворяет и этому условию.
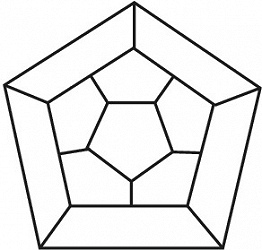
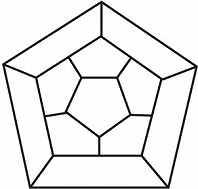
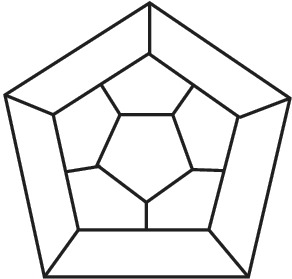
В 1859 У. Гамильтон предложил головоломку «Кругосветное путешествие», состоящую в отыскании такого пути, проходящего через все вершины (их можно интерпретировать как городá) графа, изображённого на рис. 2, чтобы посетить каждую вершину только один раз и вернуться в исходную вершину. Пути в графах, обладающие таким свойством, называются гамильтоновыми циклами. Необходимые и достаточные условия существования гамильтонова цикла в графе неизвестны. Задача о гамильтоновых циклах в графе получила разл. обобщения. Одно из них – задача коммивояжёра, имеющая ряд приложений в исследовании операций, в частности при решении некоторых транспортных проблем. Она состоит в следующем: имеется некоторое количество городов, расстояния между которыми известны; нужно найти кратчайший замкнутый путь, проходящий через все города.
В 1847 англ. математик Т. Киркман поставил и решил задачу о 15 школьницах, которые должны гулять ежедневно пятью группами по трое в каждой группе. Необходимо так составить расписание для их прогулок, чтобы каждая школьница в течение семи дней точно один раз попадала в одну группу с каждой из остальных. Эта задача связана с задачей, поставленной швейц. математиком Я. Штейнером (1853), о построении систем троек. Системой троек Штейнера порядка $v $называется такой набор троек из множества, содержащего $v$ элементов, что каждая пара элементов входит точно в одну тройку. Системы троек Штейнера описаны для $v⩽15 $. Оказывается, что для $ v=3, 7, 9 $ системы троек единственны с точностью до эквивалентности (до перестановки $v$ элементов и перестановки троек); для $v=13 $ существуют две неэквивалентные системы троек; при $v=15 $ таких троек $80 $. Для $v>15 $ число разл. систем троек Штейнера неизвестно.
Классич. задача о встречах состоит в следующем. Имеются две одинаковые колоды карт из $n$ разл. карт каждая. Необходимо определить число расположений карт $D_{nr}, r=0,1,… n, $ во второй колоде таких, что при сравнении соответствующих карт первой и второй колоды число совпадений равно $r$. Частный случай этой задачи при $r=0 $ впервые был сформулирован франц. учёным П. де Монмором в нач. 18 в.
К К. з. к. относится т. н. задача о супружеских парах, которая состоит в определении числа рассаживаний $n$ супружеских пар на $2n$ местах за круглым столом так, чтобы ни один муж не сидел рядом со своей женой.
Задача о числе разбиений натурального числа $n$ на слагаемые появилась в письме Г. В. Лейбница к Я. Бернулли (1669). Разработка методов решения задач такого типа была осуществлена Эйлером, который эффективно использовал для этой цели производящие функции.
Классич. задача размещения состоит в определении числа $C_{nm} (r)$ способов размещения $m $ разл. предметов в $n$ разл. ячейках с заданным числом $r$ пустых ячеек. Оказывается, что$$C_{nm}(r)=c_n^rΔ^{n-r}0^m, r=0,1,…, n, $$где
$$Δ^k0^m=\sum_{j=0}^k (-1)^jC_k^j (k-j)^m. $$
Эта задача имеет разл. теоретико-вероятностные приложения. При этом в осн. получаются асимптотич. результаты, когда $m$ и $n $ неограниченно возрастают.