ГРА́ФОВ ТЕО́РИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
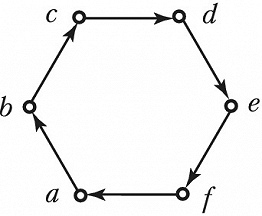
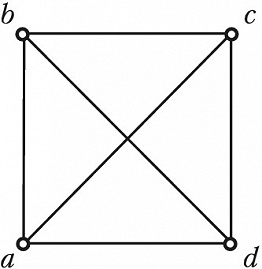
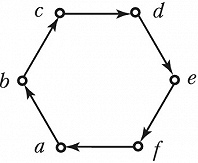
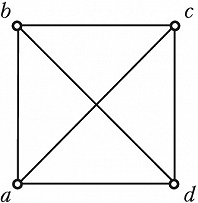
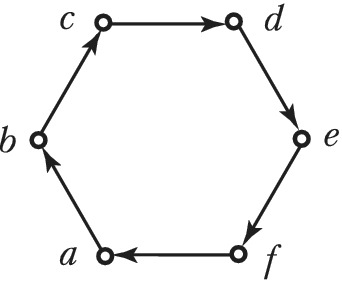
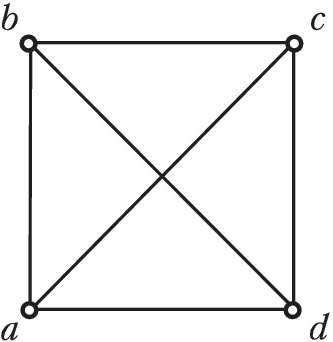
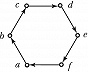
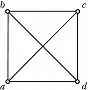
ГРА́ФОВ ТЕО́РИЯ, раздел дискретной математики, в котором изучаются свойства графов и их обобщений. Графом называется пара ($V, E$), где $V$ – множество точек, называемых вершинами, и $E$ – множество пар вершин, причём если порядок, в котором перечислены вершины в паре, не важен, то эта пара вершин графа называется ребром, а если важен – дугой. Граф, содержащий только рёбра, называется неориентированным графом, или просто графом, а граф, содержащий только дуги, – ориентированным графом. На рис. 1 – неориентированный граф с вершинами $a, b, c, d$ и рёбрами $(a, b), (b, c), (c, d), (a, d), (a, c), (b, d)$, на рис. 2 – ориентированный граф с вершинами $a, b, c, d, e, f$ и дугами $(a, b), (b, c), (c, d), (d, e), (e, f), (f, a)$.
Исторический очерк
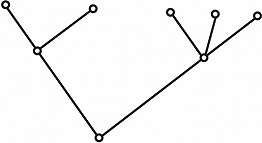
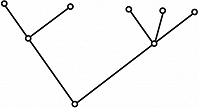
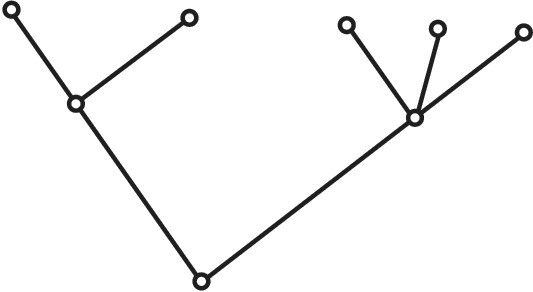
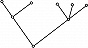
Первые задачи Г. т. были связаны с решением математич. задач развлекательного характера и головоломок (см. Комбинаторные задачи классические). Одним из первых результатов Г. т. был критерий существования обхода всех рёбер графа без повторений, полученный Л. Эйлером (1736) при решении задачи о Кёнигсбергских мостах (см. Гамильтонов цикл). С сер. 19 в. появляются относящиеся к Г. т. работы, содержащие результаты, связанные с разл. приложениями математики. Так, Г. Кирхгоф (1847) для составления полной системы уравнений для токов и напряжений в электрич. сетях (см. Кирхгофа правила) предложил представлять такую сеть графом и находить в этом графе остовные деревья, что приводит к решению задачи выделения независимых систем уравнений. Деревом называется связный граф, не содержащий циклов (рис. 3), остовное дерево графа – это его подграф, представляющий собой дерево, множество вершин которого совпадает с множеством вершин графа. А. Кэли (1854) для подсчёта числа изомеров предельных углеводородов пришёл к задачам описания и перечисления деревьев, обладающих заданными свойствами. Термин «граф» утвердился в математике после выхода монографии нем. математика Д. Кёнига (1936). Начиная со 2-й пол. 20 в. значительно расширились исследования в Г. т., в осн. в силу развития дискретной математики и вычислит. техники. Задание графа равносильно заданию на элементах множества вершин $V$ некоторого бинарного отношения. По этой причине, а также ввиду возможности наглядного представления графа в виде чертежа на плоскости, графовые модели используются при построении алгоритмов решения разнообразных задач как в математике и естествознании, так и в гуманитарных науках.
Методы исследования в теории графов
Прежде всего выделяются комбинаторные методы теоретико-множественного анализа заданного бинарного отношения на множестве вершин. Весьма существенны (особенно в перечислительных задачах) алгебраические методы, в первую очередь методы теории групп (в частности, групп подстановок). При изучении укладок графа на плоскость привлекаются результаты топологич. характера. Случайные графы изучаются с помощью теоретико-вероятностных методов.
Особую роль при изучении графов играют матричные методы. Для графа $G$ матрицей смежности $A=A(G)=||a_{ij}||$ называется матрица, в которой $a_{ij}=1$, если в графе $G$ вершина $i$ связана с вершиной $j$ ребром (или дугой в ориентированном графе) и $a_{ij}=0$ в противном случае. В первом случае говорят, что вершины $i$ и $j$ смежны, во втором случае – что они несмежны. Маршрутом в графе $G$ называется последовательность $v_0e_1v_1…v_{n–1}e_nv_n$, состоящая попеременно из вершин и рёбер графа, в которой ребро $e_i$ соединяет вершины $v_{i–1}$ и $v_i, i=1, …, n$; говорят, что этот маршрут связывает вершины $v_0$ и $v_n$. Маршрут, в котором $v_0=v_n$, называется циклом. Маршрут называется цепью (соответственно, простой цепью), если все его рёбра (все его вершины) различны. При $n⩾1$ элемент на месте $(i, j)$ в матрице $A^n$ равен числу маршрутов длины $n$ из вершины $v_i$ в вершину $v_j$. Граф называется связным, если для любых его двух вершин существует маршрут, связывающий эти вершины. Для графа $G$ с $p$ вершинами и $q$ рёбрами, в котором занумерованы как вершины, так и рёбра, рассматривается матрица инцидентности $B(G)$, представляющая собой матрицу, состоящую из нулей и единиц с двумя единицами в каждом столбце; в столбце, соответствующем ребру, соединяющему вершины $i$ и $j$, единица стоит в строках с номерами $i$ и $j$. Говорят, что каждая из вершин $i$ и $j$ и соединяющее их ребро инцидентны, два ребра смежны, если они имеют общую инцидентную им вершину. Ранг матрицы инцидентности $B(G)$ равен $p-1$, если граф $G$ является связным графом.
Множество собств. значений матрицы смежности графа или ориентированного графа (при этом каждое значение берётся столько раз, какова его кратность) называется спектром графа. Спектр графа с $n$ вершинами состоит из $n$ действительных чисел. Изучение спектра графа позволяет выяснить мн. особенности его строения.
Задачи теории графов
Центральным в Г. т. является раздел, изучающий структурные свойства графов. Одной из характеристик структуры графа является последовательность степеней его вершин. Степенью вершины неориентированного графа называется число инцидентных ей рёбер. Графич. разбиением чётного натурального числа $n$ называется представление его в виде суммы $p$ слагаемых $n=\sum_{i=1}^d d_i$ такое, что существует граф с $p$ вершинами, степени которых равны $d_1,…,d_p$. В Г. т. известен эффективный алгоритм, позволяющий для данного упорядоченного набора чисел $(d_1,…,d_p)$ определить, существует ли граф с $p$ вершинами $v_1,…,v_p$, для которых последовательность степеней $(d(v_1),…,d(v_p))$ совпадает с этим набором. Подробно изучено др. важное структурное свойство – связность графа, а также вопросы, относящиеся к существованию в связном графе маршрутов определённого вида.
Спец. разделом структурной Г. т. является факторизация графа, т. е. разложение графа $G= (V, E)$ на сумму факторов (подграфов) $G_1, …, G_m$ с некоторым заданным свойством, где $G_i=(V, E_i)$ и $E=E_1\cup …\cup E_m$ – разбиение множества рёбер на непустые непересекающиеся подмножества. Наиболее распространённые виды факторизации: n-факторизация, где $G_i$ – однородные графы степени $n$ (графы, степени всех вершин которых одинаковы и равны $n$), и древесная факторизация, где каждая компонента любого $G_i, i=1,…,m,$ является деревом. Любой полный граф $K_{2n}$, т. е. граф, в котором любые две вершины смежны, 1-факторизуем, но не 2-факторизуем; любой полный граф $K_{2n+1}$ не является 1-факторизуемым, но представляется в виде суммы $n$ факторов, являющихся циклами. Если при 1-факторизации речь идёт о возможности разбиения множества рёбер на подмножества, состоящие из попарно несмежных рёбер (при этом каждое из подмножеств есть 1-фактор), то всякое разбиение множества вершин графа на $n$ подмножеств таких, что вершины из любых двух разных подмножеств попарно несмежны, определяет правильную раскраску графа в $n$ цветов. Теория раскрасок графа возникла и развивалась в связи с четырёх красок задачей, которая получила решение лишь на рубеже 1970–80-х гг.
С графом $G=(V, E)$ естественно связывается целый ряд графов, напр. его подграфы, дополнительный граф, рёберный граф $L(G)$. Рёберным для графа $G$ с $p$ вершинами и $q$ рёбрами называется граф с множеством вершин $E$, в котором две вершины соединены ребром тогда и только тогда, когда соответствующие рёбра смежны в $G$. Критерий того, что данный граф является рёберным графом, заключается в отсутствии у него подграфов, принадлежащих множеству из 9 конкретно указанных графов (с 4, 5 или 6 вершинами). Изучение спец. классов графов, выделяемых к.-л. определяющим признаком или структурным свойством, составляет одно из направлений теории графов.
Если граф задан бинарным отношением на множестве, то часто возникает вопрос о том или ином его конкретном представлении. Такого рода задачей является задача о планарности графа, т. е. о возможности представить его на плоскости рисунком, в котором нет пересечения рёбер. Наиболее известный критерий планарности даёт теорема Понтрягина – Куратовского: граф является планарным тогда и только тогда, когда он не содержит в качестве подграфа ни полного графа $K_5$, ни двудольного графа $K_{3,3}$. Граф $G=(V, E)$ называется двудольным, если допускается разбиение вершин множества $V$ на два подмножества $V_1$ и $V_2$, состоящие из попарно несмежных вершин, такой граф обозначается , где $n_i$ – число вершин в подмножестве $V_i, i=1, 2$.
Значит. часть исследований в Г. т. составляют перечислительные и экстремальные задачи. Отд. класс экстремальных задач – задачи о покрытии. Осн. объектами исследования в задачах о покрытии являются четыре важнейшие теоретико-графовые константы: число вершинного покрытия $α_0$, число рёберного покрытия $α_1$, вершинное число независимости $β_0$ и рёберное число независимости $β_1$. Число вершинного покрытия графа $G$ есть миним. число вершин в покрывающем множестве, т. е. в таком множестве вершин, для которого каждое ребро графа $G$ инцидентно хотя бы одной вершине этого множества. Вершинное число независимости графа $G$ есть наибольшее возможное число элементов в независимом множестве, т. е. в таком множестве вершин, в котором любые две вершины несмежны. Аналогично определяются число рёберного покрытия и рёберное число независимости. Для любого связного графа $G$ с $p>1$ вершинами $α_0+β_0=α_1+β_1=p$, а для двудольного графа $β_1=α_0$. Значения этих констант известны лишь для некоторых графов частного вида. К задачам о покрытии тесно примыкает теория доминирования. В ней рассматриваются доминирующие множества графа $G=(V, E)$, т. е. такие подмножества $D \subset V$, что любая вершина из $V\setminus D$ смежна хотя бы с одной из вершин $D$. Важнейшей константой графа является число доминирования – наименьшее возможное число вершин в его доминирующем множестве.