ПРЕЦЕ́ССИЯ

Рис. 1. Прецессия гироскопа.

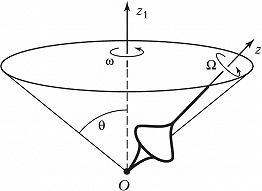
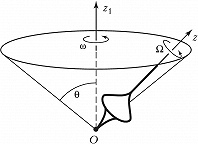
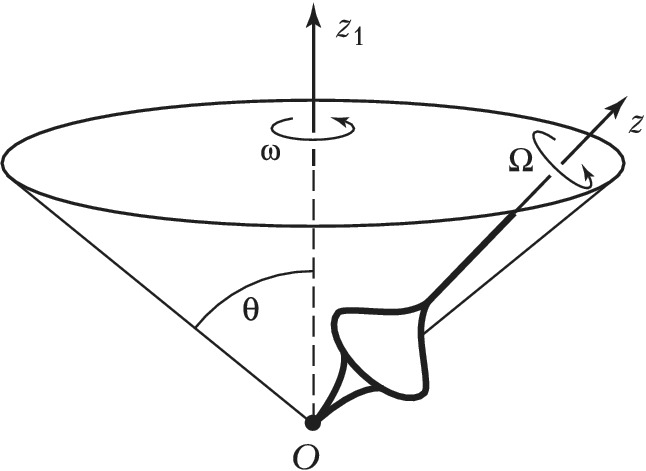
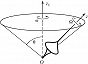
ПРЕЦЕ́ССИЯ (позд­не­ла­тин­ское praeces­sio – дви­же­ние впе­ре­ди, от лат. prae­ce­do – ид­ти впе­ре­ди, пред­ше­ст­во­вать), од­на из со­став­ляю­щих вра­ща­тель­но­го дви­же­ния твёр­до­го те­ла (на­ря­ду с собств. вра­ще­ни­ем и ну­та­ци­ей). Пред­став­ля­ет со­бой вра­ще­ние оси $Oz$ (оси соб­ств. вра­ще­ния те­ла) во­круг оси $Oz_1$, со­хра­няю­щей свою ори­ен­та­цию в про­стран­ст­ве (рис. 1). При этом уг­ло­вая ско­рость собств. вра­ще­ния $Ω$ и уг­ло­вая ско­рость П. $ω$ от­лич­ны от ну­ля, угол ме­ж­ду ося­ми $Oz$ и $Oz_1$ (т. н. угол ну­та­ции $θ$) ос­та­ёт­ся по­сто­ян­ным [$θ(t)≡const≠0$], а ось $Oz$ опи­сы­ва­ет во­круг оси $Oz_1$ пря­мой кру­го­вой ко­нус. Ес­ли по­сто­ян­ны так­же ве­ли­чи­ны $Ω$ и $ω$, то П. на­зы­ва­ет­ся ре­гу­ляр­ной; в этом слу­чае ак­сои­ды так­же пред­став­ля­ют со­бой кру­го­вые ко­ну­сы.

П. на­блю­да­ет­ся, напр., при не­ко­то­рых вра­ще­ни­ях ги­ро­ско­па. Ес­ли мо­мент всех при­ло­жен­ных к не­му сил от­но­си­тель­но не­под­виж­ной точ­ки $О$ ра­вен ну­лю, то при про­из­воль­ных на­чаль­ных ус­ло­ви­ях дви­же­ния век­тор ки­не­тич. мо­мен­та $\boldsymbol G$ те­ла по­стоя­нен, а ось сим­мет­рии $Oz$ те­ла в на­ча­ле дви­же­ния мо­жет не сов­па­дать с век­то­ром $\boldsymbol G$. В этом слу­чае ось $Oz$ со­вер­ша­ет вра­ще­ние во­круг не­под­виж­но­го век­то­ра $\boldsymbol G$, с ко­то­рым свя­за­на не­по­движ­ная ось $Oz_1$, т. е. ги­ро­скоп со­вер­ша­ет ре­гу­ляр­ную П. Ве­ли­чи­ны $Ω$ и $ω$ свя­за­ны со­от­но­ше­ни­ем $ω·(A-C)·\cos θ=CΩ$, где $A$ и $C$ со­от­вет­ст­вен­но эк­ва­то­ри­аль­ный и осе­вой мо­мен­ты инер­ции те­ла, при­чём $A≠C$ и $\cos θ≠0$. Для ги­ро­ско­па, со­вер­шаю­ще­го собств. вра­ще­ние с боль­шой уг­ло­вой ско­ро­стью $Ω$, П. на­зы­ва­ет­ся бы­ст­рой, т. к. при $\cos θ≠0$ ве­ли­чи­на $ω$ име­ет тот же по­ря­док, что и $Ω$. При $θ=π/2$ П. пе­ре­хо­дит в про­стое вра­ще­ние те­ла во­круг век­то­ра $\boldsymbol G$ с уг­ло­вой ско­ро­стью $ω$.

Ес­ли си­ла тя­же­сти, при­ло­жен­ная к сим­мет­рич­но­му те­лу (напр., волч­ку) в точ­ке, ле­жа­щей на оси сим­мет­рии, соз­да­ёт мо­мент от­но­си­тель­но точ­ки $O$, то те­ло при спец. на­чаль­ных ус­ло­ви­ях дви­же­ния мо­жет со­вер­шать ре­гу­ляр­ную П., в ко­то­рой его ось сим­мет­рии вра­ща­ет­ся во­круг вер­ти­ка­ли с уг­ло­вой ско­ро­стью $ω$. При вра­ще­нии волч­ка, как пра­ви­ло, на­блю­да­ет­ся дви­же­ние, близ­кое к мед­лен­ной ре­гу­ляр­ной П., т. к. $ω≈Pa/CΩ$, где $P$ – вес те­ла, $a$ – рас­стоя­ние ме­ж­ду точ­кой $O$ и цен­тром тя­же­сти те­ла. В этом слу­чае век­тор ки­не­тич. мо­мен­та $\boldsymbol G$ те­ла так­же со­вер­ша­ет вра­ще­ние во­круг вер­ти­каль­ной оси $Oz_1$ с уг­ло­вой ско­ро­стью $ω$. Од­на­ко в ре­аль­но­сти на­чаль­ные ус­ло­вия, как пра­ви­ло, от­ли­ча­ют­ся от вы­ше­упо­мя­ну­тых, по­это­му ча­ще все­го на­блю­да­ет­ся т. н. псев­до­ре­гу­ляр­ная П.: мед­лен­ный по­во­рот век­то­ра $\boldsymbol G$ со­че­та­ет­ся с бы­ст­рой П., при ко­то­рой ось $Oz$ те­ла вра­ща­ет­ся во­круг век­то­ра $\boldsymbol G$. В этом дви­же­нии из­ме­ня­ет­ся угол $θ$, т. е. про­ис­хо­дит ну­та­ция.

Рис. 2. Силы, вызывающие прецессию Земли. S – Солнце, PN – северный полюс мира, ΠN и ΠS – северный и южный полюсы эклиптики. Синей штриховой линией показано сферическое приближение формы Земли, голубо...

П. в ас­тро­но­мии, из­ме­не­ние на­прав­ле­ния век­то­ра уг­ло­во­го (ки­не­ти­че­ско­го) мо­мен­та не­бес­но­го те­ла под дей­ст­ви­ем мо­мен­та внеш­ней си­лы. Наи­бо­лее изу­че­на П. Зем­ли под дей­ст­ви­ем сил при­тя­же­ния Лу­ны и Солн­ца. П. Зем­ли бы­ла от­кры­та Гип­пар­хом во 2 в. до н. э. и на­зва­на пред­ва­ре­ни­ем рав­но­ден­ст­вий (т. к. вслед­ст­вие П. Зем­ли точ­ки осен­не­го и ве­сен­не­го рав­но­ден­ст­вий мед­лен­но сме­ща­ют­ся по эк­лип­ти­ке на­встре­чу Зем­ле в её дви­же­нии во­круг Солн­ца и но­вое рав­но­ден­ст­вие на­сту­па­ет рань­ше, чем Зем­ля опи­шет пол­ный круг). Фи­зи­ко-ма­те­ма­тич. объ­яс­не­ние П. впер­вые дал И. Нью­тон в 1686. Тео­рия П. раз­ви­та в 18 в. в ра­бо­тах Ж. Д’Алам­бера, П. Ла­п­ла­са и Л. Эй­ле­ра. Точ­ные чи­сло­вые зна­че­ния осн. ве­ли­чин, ха­рак­те­ри­зую­щих П. Зем­ли, оп­ре­де­ле­ны Ф. Бес­се­лем в нач. 19 в. (на ос­но­ве на­блю­де­ний).

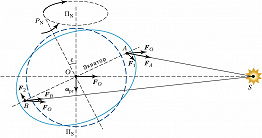
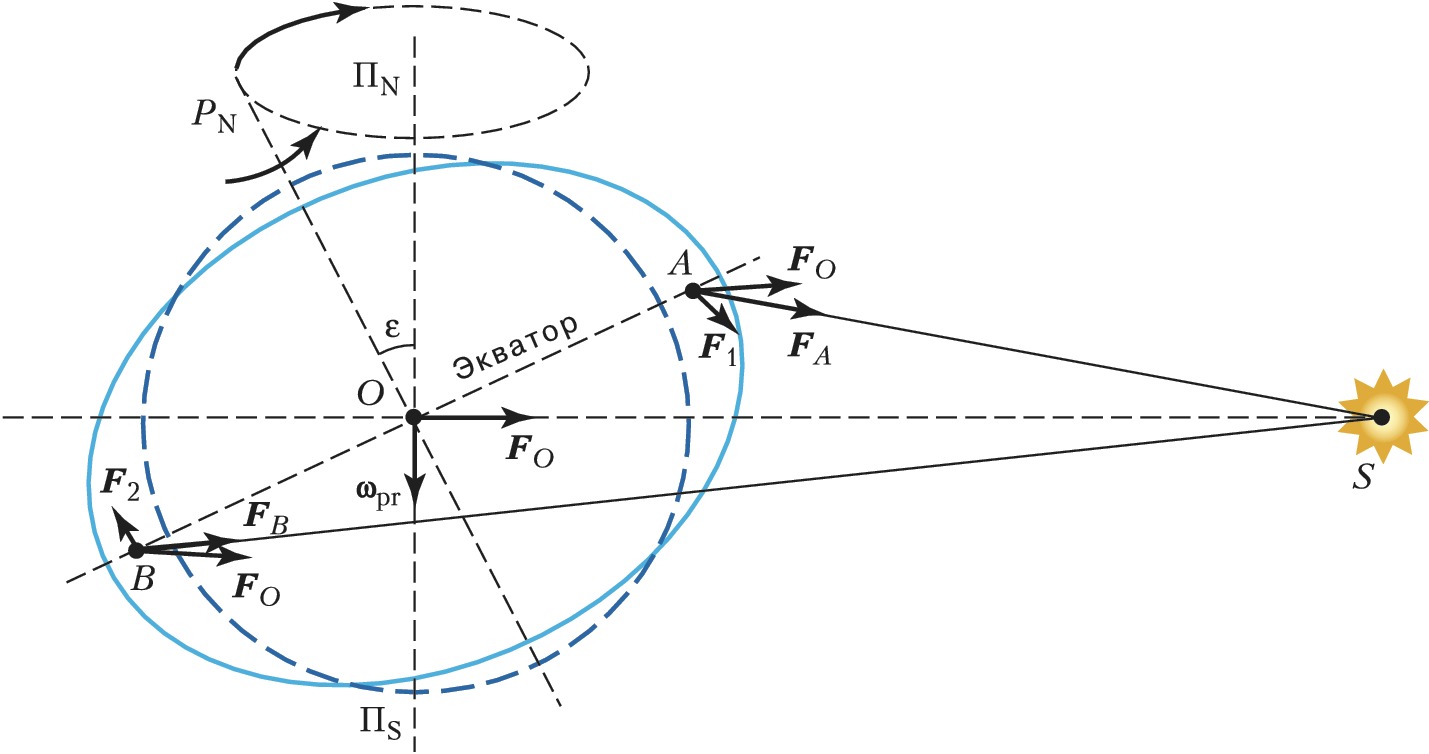
П. Зем­ли вы­зва­на её не­сфе­рич­но­стью и не­сов­па­де­ни­ем плос­ко­стей эк­ва­то­ра и эк­лип­ти­ки. Эк­ва­то­ри­аль­ный ра­ди­ус Зем­ли боль­ше по­ляр­но­го, по­это­му гра­ви­тац. при­тя­же­ние Лу­ной или Солн­цем эк­ва­то­ри­аль­но­го из­быт­ка масс Зем­ли вы­зы­ва­ет мо­мент сил, стре­мя­щий­ся со­вмес­тить плос­ко­сти эк­ва­то­ра и эк­лип­ти­ки (рис. 2). Рас­смат­ри­вая гра­ви­тац. воз­дей­ст­вие Солн­ца $S$ на не­сфе­рич. Зем­лю, мож­но вы­де­лить си­лу $\boldsymbol F_O$, дей­ст­вую­щую на центр масс Зем­ли $O$, и си­лы $\boldsymbol F_1$ и $\boldsymbol F_2$, дей­ст­вую­щие на эк­ва­то­ри­аль­ный из­бы­ток масс и оп­ре­де­ляе­мые вы­ра­же­ния­ми $\boldsymbol F_1=\boldsymbol F_A-\boldsymbol F_O$ и $\boldsymbol F_2=\boldsymbol F_B-\boldsymbol F_O$, где $\boldsymbol F_A$ и $\boldsymbol F_B$ – си­лы, дей­ст­вую­щие со сто­ро­ны Солн­ца на точ­ки $A$ и $B$ (цент­ры масс эк­ва­то­ри­аль­но­го из­быт­ка масс в дан­ном се­че­нии). Па­ра сил $\boldsymbol F_1$ и $\boldsymbol F_2$ стре­мит­ся по­вер­нуть плос­кость эк­ва­то­ра $AB$ по ча­со­вой стрел­ке (мо­мент сил на­прав­лен пер­пен­ди­ку­ляр­но плос­ко­сти ри­сун­ка от чи­та­те­ля). Из-за вра­ще­ния Зем­ли во­круг сво­ей оси $OP_N$ та­ко­го по­во­ро­та не про­ис­хо­дит, но ори­ен­та­ция оси $OP_N$ из­ме­ня­ет­ся: она опи­сы­ва­ет в про­стран­ст­ве ко­нус во­круг оси $ОП_N$, пер­пен­ди­ку­ляр­ной плос­ко­сти ор­би­ты Зем­ли. Угол ε ме­ж­ду осью вра­ще­ния Зем­ли $OP_N$ и осью $ОΠ_N$ ра­вен уг­лу на­кло­на эк­лип­ти­ки к эк­ва­то­ру (ок. 23,5°).

На ри­сун­ке пред­став­ле­но рас­по­ло­же­ние Зем­ли и Солн­ца при зим­нем солн­це­стоя­нии. Во вре­мя солн­це­стоя­ний мо­мент сил $\boldsymbol F_1$ и $\boldsymbol F_2$ мак­си­ма­лен; сле­до­ва­тель­но, и мгно­вен­ная уг­ло­вая ско­рость $ω_{pr}$ П. мак­си­маль­на. Во вре­мя рав­но­ден­ст­вий мо­мент сил $\boldsymbol F_1$ и $\boldsymbol F_2$ ра­вен ну­лю и $ω_{pr}= 0$.

В ре­аль­но­сти мгно­вен­ная уг­ло­вая ско­рость П. скла­ды­ва­ет­ся из двух осн. час­тей, обу­слов­лен­ных мо­мен­та­ми сил при­тя­же­ния Солн­ца и Лу­ны. В ре­зуль­та­те это­го сум­мар­но­го эф­фек­та сев. по­люс ми­ра опи­сы­ва­ет на не­бес­ной сфе­ре кри­вую, близ­кую к ок­руж­но­сти с уг­ло­вым ра­диу­сом ок. 23,5°. Пе­ри­од обо­ро­та со­став­ля­ет ок. 25765 лет. Век­тор $\boldsymbol \omega_{pr}$ на­прав­лен к точ­ке $Π_S$, по­это­му пре­цес­си­он­ное дви­же­ние оси $OP_N$ про­ис­хо­дит по ча­со­вой стрел­ке, ес­ли смот­реть с сев. по­лю­са эк­лип­ти­ки: точ­ка ве­сен­не­го рав­но­ден­ст­вия сме­ща­ет­ся по эк­лип­ти­ке на­встре­чу Солн­цу со ско­ро­стью ок. 50,3″ в год.

Рас­смат­ри­вае­мые си­лы при­тя­же­ния и их мо­мен­ты из­ме­ня­ют­ся во вре­ме­ни из-за об­ра­ще­ния Зем­ли во­круг Солн­ца и Лу­ны во­круг Зем­ли. Это при­во­дит к пе­рио­дич. дви­же­ни­ям век­то­ра уг­ло­во­го мо­мен­та Зем­ли, ко­то­рые на­кла­ды­ва­ют­ся на мед­лен­ное пре­цес­си­он­ное дви­же­ние и на­зы­ва­ют­ся ну­та­ци­ей в ас­тро­но­мии.

Мо­мент сил, вы­зы­ваю­щий П., про­пор­цио­на­лен $r^{–3}$, где $r$ – рас­стоя­ние от Зем­ли до ис­точ­ни­ка внеш­ней си­лы. По­это­му гл. роль в пре­цес­си­он­ном дви­же­нии по­лю­са ми­ра иг­ра­ет бли­жай­шее к Зем­ле не­бес­ное те­ло – Лу­на (её влия­ние при­мер­но в 2 раза боль­ше влия­ния Солн­ца). При­тя­же­ние эк­ва­то­ри­аль­но­го из­быт­ка масс Зем­ли др. пла­не­та­ми Сол­неч­ной сис­те­мы так­же долж­но вы­зы­вать пре­цес­си­он­ное дви­же­ние оси ми­ра. Од­на­ко из-за боль­шой уда­лён­но­сти пла­нет их влия­ние ма­лó (макс. ам­пли­ту­ды гар­мо­ник не пре­вы­ша­ют 0,25 мс ду­ги). Тем не ме­нее в совр. тео­ри­ях пре­цес­сии – ну­та­ции Зем­ли пла­нет­ная П. так­же учи­ты­ва­ет­ся.

Го­раз­до боль­шее влия­ние пла­не­ты ока­зы­ва­ют на по­ло­же­ние плос­ко­сти эк­лип­ти­ки в про­стран­ст­ве: пла­не­ты вы­зы­ва­ют воз­му­ще­ния ор­би­ты Зем­ли, т. е. из­ме­не­ние по­ло­же­ния в про­стран­ст­ве век­то­ра ор­би­таль­но­го уг­ло­во­го мо­мен­та сис­те­мы Зем­ля – Лу­на. В ре­зуль­та­те по­люс эк­лип­ти­ки $Π_N$ сме­ща­ет­ся при­мер­но на 0,5g в год, что при­во­дит к до­пол­нит. дви­же­нию точ­ки ве­сен­не­го рав­но­ден­ст­вия на­встре­чу Солн­цу на 12″ в сто­ле­тие и умень­ше­нию на­кло­на эк­лип­ти­ки к эк­ва­то­ру на 47″ в сто­ле­тие. Это сме­ще­ние по­лю­са эк­лип­ти­ки на­зы­ва­ют П. от пла­нет.