ГИРОСКО́П

ГИРОСКО́П (от греч. γῦρος – круг, ок­руж­ность и σϰοπέω – на­блю­дать), уст­рой­ст­во, со­вер­шаю­щее бы­ст­рые цик­ли­че­ские (вра­ща­тель­ные или ко­ле­ба­тель­ные) дви­же­ния и чув­ст­ви­тель­ное вслед­ст­вие это­го к по­во­ро­ту в инер­ци­аль­ном про­стран­ст­ве. Тер­мин «Г.» пред­ло­жен в 1852 Ж. Б. Л. Фу­ко для изо­бре­тён­но­го им при­бо­ра, пред­на­зна­чен­но­го для де­мон­ст­ра­ции вра­ще­ния Зем­ли во­круг сво­ей оси. Дол­гое вре­мя тер­мин «Г.» ис­поль­зо­вал­ся для обо­зна­че­ния бы­ст­ров­ра­щаю­ще­го­ся сим­мет­рич­но­го твёр­до­го те­ла. В совр. тех­ни­ке Г. – осн. эле­мент все­воз­мож­ных ги­ро­ско­пич. уст­ройств или при­бо­ров, ши­ро­ко при­ме­няе­мых для ав­то­ма­тич. управ­ле­ния дви­же­ни­ем са­мо­лё­тов, су­дов, тор­пед, ра­кет, кос­мич. ап­па­ра­тов, мо­биль­ных ро­бо­тов, для це­лей на­ви­га­ции (ука­за­те­ли кур­са, по­во­ро­та, го­ри­зон­та, стран све­та), для из­ме­ре­ния уг­ло­вой ори­ен­та­ции под­виж­ных объ­ек­тов и во мно­гих др. слу­ча­ях (напр., при про­хо­ж­де­нии ство­лов што­лен, строи­тель­ст­ве мет­ро­по­ли­те­нов, при бу­ре­нии сква­жин).

Классический гироскоп

Со­глас­но за­ко­нам нью­то­нов­ской ме­ха­ни­ки ско­рость по­во­ро­та оси бы­ст­ров­ра­щаю­ще­го­ся сим­мет­рич­но­го твёр­до­го те­ла в про­стран­ст­ве об­рат­но про­пор­цио­наль­на его собств. уг­ло­вой ско­ро­сти и, сле­до­ва­тель­но, ось Г. по­во­ра­чи­ва­ет­ся столь мед­лен­но, что на не­ко­то­ром ин­тер­ва­ле вре­ме­ни её мож­но ис­поль­зо­вать в ка­че­ст­ве ука­за­те­ля не­из­мен­но­го на­прав­ле­ния в про­стран­ст­ве.

Рис. 1. Прецессия гироскопа. Угловая скорость прецессии 𝛚 направлена так, что вектор собственного кинетического момента H стремится к совмещению с вектором момента M пары сил {P, P'}, P'=–P, дей...

Рис. 2. Классический гироскоп в кардановом подвесе: 1 – внешнее кольцо; 2 – внутреннее кольцо; 3 – ротор.

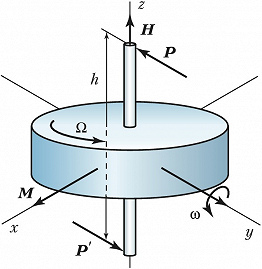
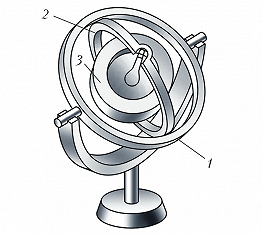
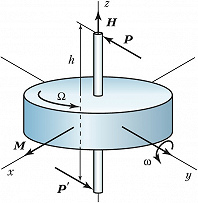
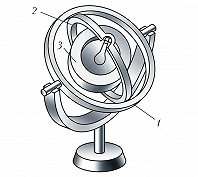
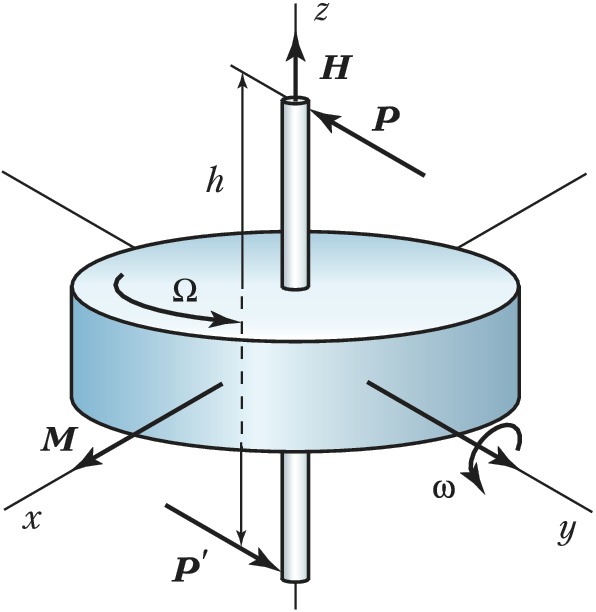
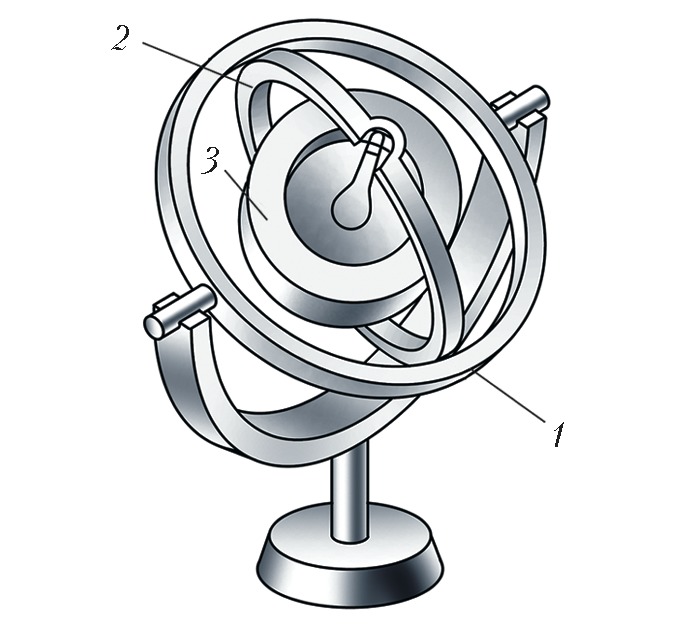
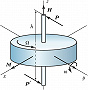
Про­стей­шим Г. яв­ля­ет­ся вол­чок, па­ра­док­саль­ность по­ве­де­ния ко­то­ро­го за­клю­ча­ет­ся в его со­про­тив­ле­нии из­ме­не­нию на­прав­ле­ния оси вра­ще­ния. Под воз­дей­ст­ви­ем внеш­ней си­лы ось волч­ка на­чи­на­ет дви­гать­ся в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном век­то­ру си­лы. Имен­но бла­го­да­ря это­му свой­ст­ву вра­щаю­щий­ся вол­чок не па­да­ет, а его ось опи­сы­ва­ет ко­нус во­круг вер­ти­ка­ли. Это дви­же­ние на­зы­ва­ет­ся пре­цес­си­ей Г. Ес­ли к оси бы­ст­ро вра­щаю­ще­го­ся сво­бод­но­го Г. при­ло­жить па­ру сил $\{\boldsymbol P, \boldsymbol P′\}, \boldsymbol P′=– \boldsymbol P$, с мо­мен­том $M=Ph$, где $h$ – пле­чо па­ры сил (рис. 1), то (про­тив ожи­да­ния) Г. нач­нёт до­пол­ни­тель­но по­во­ра­чи­вать­ся не во­круг оси $x$, пер­пен­ди­ку­ляр­ной к плос­ко­сти па­ры сил, а во­круг оси $y$, ле­жа­щей в этой плос­ко­сти и пер­пен­ди­ку­ляр­ной оси $z$ вра­ще­ния Г. Ес­ли в к.-л. мо­мент вре­ме­ни дей­ст­вие па­ры сил пре­кра­тит­ся, то од­но­вре­мен­но пре­кра­тит­ся пре­цес­сия, т. е. пре­цес­си­он­ное дви­же­ние Г. безы­нер­ци­он­но. Что­бы ось Г. мог­ла сво­бод­но по­во­ра­чи­вать­ся в про­стран­ст­ве, Г. обыч­но за­кре­п­ля­ют в коль­цах кар­да­но­во­го под­ве­са (рис. 2), ко­то­рый пред­став­ля­ет со­бой сис­те­му твёр­дых тел (ра­мок, ко­лец), по­сле­до­ва­тель­но со­еди­нён­ных ме­ж­ду со­бой ци­лин­д­рич. шар­ни­ра­ми. Обыч­но при от­сут­ст­вии тех­но­ло­гич. по­греш­но­стей оси ра­мок кар­да­но­во­го под­ве­са пе­ре­се­ка­ют­ся в од­ной точ­ке – цен­тре под­ве­са. За­кре­п­лён­ное в та­ком под­ве­се сим­мет­рич­ное те­ло вра­ще­ния (ро­тор) име­ет три сте­пе­ни сво­бо­ды и мо­жет со­вер­шать лю­бой по­во­рот во­круг цен­тра под­ве­са. Г., у ко­то­ро­го центр масс сов­па­да­ет с цен­тром под­ве­са, на­зы­ва­ет­ся урав­но­ве­шен­ным, ас­та­ти­че­ским или сво­бод­ным. Изу­че­ние за­ко­нов дви­же­ния клас­сич. Г. – за­да­ча ди­на­ми­ки твёр­до­го те­ла.

Осн. ко­ли­че­ст­вен­ной ха­рак­те­ри­сти­кой ро­то­ра ме­ха­нич. Г. яв­ля­ет­ся его век­тор собств. ки­не­тич. мо­мен­та, на­зы­вае­мо­го так­же мо­мен­том ко­ли­че­ст­ва дви­же­ния или мо­мен­том им­пуль­са, $$\boldsymbol H=I\boldsymbol{\Omega}, \,\,\,(1)$$где $I$ – мо­мент инер­ции ро­то­ра Г. от­но­си­тель­но оси собств. вра­ще­ния, $\boldsymbol \Omega$ – уг­ло­вая ско­рость собств. вра­ще­ния Г. от­но­си­тель­но оси сим­мет­рии.

Мед­лен­ное дви­же­ние век­то­ра собств. ки­не­тич. мо­мен­та Г. под дей­ст­ви­ем мо­мен­тов внеш­них сил, на­зы­вае­мое пре­цес­си­ей Г., опи­сы­ва­ет­ся урав­не­ни­ем$$\boldsymbol {\omega} × \boldsymbol H=\boldsymbol M,\,\,\,(2)$$где $\boldsymbol \omega$ – век­тор уг­ло­вой ско­ро­сти пре­цес­сии, $\boldsymbol H$ – век­тор собств. ки­не­тич. мо­мен­та Г., $\boldsymbol M$ – ор­то­го­наль­ная к $\boldsymbol H$ со­став­ляю­щая век­то­ра мо­мен­та внеш­них сил, при­ло­жен­ных к ги­ро­ско­пу.

Мо­мент сил, при­ло­жен­ных со сто­ро­ны ро­то­ра к под­шип­ни­кам оси собств. вра­ще­ния ро­то­ра, воз­ни­каю­щий при из­ме­не­нии на­прав­ле­ния оси и оп­ре­де­ляе­мый урав­не­ни­ем$$\boldsymbol {M}_g=–\boldsymbol{M}=\boldsymbol H×\boldsymbol \omega,\,\,\,(3)$$на­зы­ва­ет­ся ги­ро­ско­пич. мо­мен­том.

Кро­ме мед­лен­ных пре­цес­си­он­ных дви­же­ний ось Г. мо­жет со­вер­шать бы­ст­рые ко­ле­ба­ния с ма­лой ам­пли­ту­дой и вы­со­кой час­то­той – т. н. ну­та­ции. Для сво­бод­но­го Г. с ди­на­ми­че­ски сим­мет­рич­ным ро­то­ром в бе­зы­нер­ци­он­ном под­ве­се час­то­та ну­та­ци­он­ных ко­ле­ба­ний оп­ре­де­ля­ет­ся фор­му­лой $$ν=H/A,$$где $A$ – мо­мент инер­ции ро­то­ра от­но­си­тель­но оси, ор­то­го­наль­ной оси собств. вра­ще­ния и про­хо­дя­щей че­рез центр масс ро­то­ра. При на­ли­чии сил тре­ния ну­та­ци­он­ные ко­ле­ба­ния обыч­но дос­та­точ­но бы­ст­ро за­ту­ха­ют.

По­греш­ность Г. из­ме­ря­ет­ся ско­ро­стью ухо­да его оси от пер­во­на­чаль­но­го по­ло­же­ния. Со­глас­но урав­не­нию (2) ве­ли­чи­на ухо­да, на­зы­вае­мо­го так­же дрей­фом, про­пор­цио­наль­на мо­мен­ту сил $M$ от­но­си­тель­но цен­тра под­ве­са Г.:$$ω_{yx}=M/H.\,\,\,(4)$$Уход $ω_{yx}$ обыч­но из­ме­ря­ет­ся в уг­ло­вых гра­ду­сах в час. Из фор­му­лы (4) сле­ду­ет, что сво­бод­ный Г. функ­цио­ни­ру­ет иде­аль­но лишь в том слу­чае, ес­ли внеш­ний мо­мент $M$ ра­вен 0. При этом уг­ло­вая ско­рость пре­цес­сии об­ра­ща­ет­ся в нуль и ось собств. вра­ще­ния бу­дет в точ­но­сти сов­па­дать с не­из­мен­ным на­прав­ле­ни­ем в инер­ци­аль­ном про­стран­ст­ве.

Од­на­ко на прак­ти­ке лю­бые сред­ст­ва, ис­поль­зуе­мые для под­ве­са ро­то­ра Г., яв­ля­ют­ся при­чи­ной воз­ник­но­ве­ния не­же­ла­тель­ных внеш­них мо­мен­тов не­из­вест­ных ве­ли­чи­ны и на­прав­ле­ния. Форму­ла (4) оп­ре­де­ля­ет пу­ти по­вы­ше­ния точ­но­сти ме­ха­нич. Г.: на­до умень­шить «вред­ный» мо­мент сил $M$ и уве­ли­чить ки­не­тический мо­мент $H$. При вы­бо­ре уг­ло­вой ско­ро­сти Г. не­об­хо­ди­мо учи­ты­вать од­но из главных ог­ра­ни­че­ний, свя­зан­ных с пре­де­ла­ми проч­но­сти ма­те­риа­ла ро­то­ра из-за воз­ни­каю­щих при вра­ще­нии цен­тро­беж­ных сил. При раз­го­не ро­то­ра вы­ше т. н. до­пус­кае­мой уг­ло­вой ско­ро­сти на­чи­на­ет­ся про­цесс его раз­ру­ше­ния.

Луч­шие совр. Г. име­ют слу­чай­ный уход по­ряд­ка 10^–4–10^–5 °/ч. Ось Г. с по­греш­но­стью 10^–5 °/ч со­вер­ша­ет пол­ный обо­рот на 360° за 4 тыс. лет! Точ­ность ба­лан­си­ров­ки Г. с по­греш­но­стью 10^–5 °/ч долж­на быть вы­ше од­ной де­ся­ти­ты­сяч­ной до­ли мик­ро­мет­ра (10^–10 м), т. е. сме­ще­ние цен­тра масс ро­то­ра из цен­тра под­ве­са не долж­но пре­вы­шать ве­ли­чи­ну по­ряд­ка диа­мет­ра ато­ма во­до­ро­да.

Гироскопические устройства

мож­но раз­де­лить на си­ло­вые и из­ме­ри­тель­ные. Си­ло­вые уст­рой­ст­ва слу­жат для соз­да­ния мо­мен­тов сил, при­ло­жен­ных к ос­но­ва­нию, на ко­то­ром ус­та­нов­лен ги­ро­ско­пич. при­бор; из­ме­ри­тель­ные пред­на­зна­че­ны для оп­ре­де­ле­ния па­ра­мет­ров дви­же­ния ос­но­ва­ния (из­ме­ряе­мы­ми па­ра­мет­ра­ми мо­гут быть уг­лы по­во­ро­та ос­но­ва­ния, про­ек­ции век­то­ра уг­ло­вой ско­ро­сти и т. п.).

Рис. 3. Авиационный гироуказатель курса с воздушным приводом: 1 – основание; 2 – зубчатое колесо синхронизатора; 3 – ручка арретира; 4 – арретир; 5 – шкала азимута; 6 &nd...

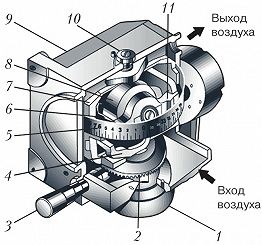
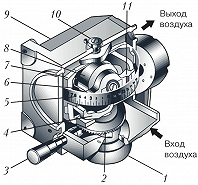
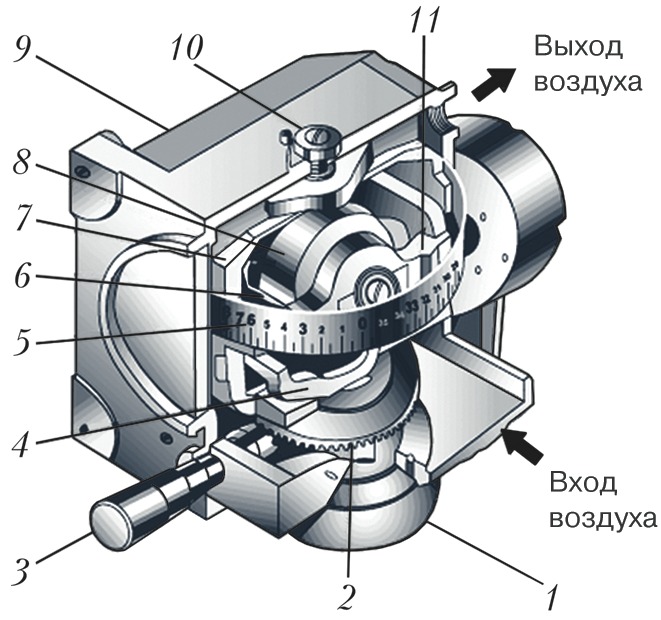
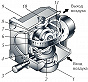
Впер­вые урав­но­ве­шен­ный Г. на­шёл прак­тич. при­ме­не­ние в 1898 в при­бо­ре для ста­би­ли­за­ции кур­са тор­пе­ды, изо­бре­тён­ном австр. ин­же­не­ром Л. Об­ри. Ана­ло­гич­ные при­бо­ры в разл. ва­ри­ан­тах ис­пол­не­ния на­ча­ли ис­поль­зо­вать в 1920-х гг. на са­мо­лё­тах для ука­за­ния кур­са (Г. на­прав­ле­ния, ги­ро­по­лу­ком­па­сы), а позд­нее для управ­ле­ния дви­же­ни­ем ра­кет. На рис. 3 по­ка­зан при­мер при­ме­не­ния ги­ро­ско­па с тре­мя сте­пе­ня­ми сво­бо­ды в ави­ац. ука­за­те­ле кур­са (ги­ро­по­лу­ком­па­се). Вра­ще­ние ро­то­ра в ша­ри­ко­под­шип­ни­ках соз­да­ёт­ся и под­дер­жи­ва­ет­ся стру­ёй сжа­то­го воз­ду­ха, на­прав­лен­ной на риф­лё­ную по­верх­ность обо­да. По шка­ле ази­му­та, при­кре­п­лён­ной к на­руж­ной рам­ке, мож­но, ус­та­но­вив ось собств. вра­ще­ния ро­то­ра па­рал­лель­но плос­ко­сти ос­но­ва­ния при­бо­ра, вве­сти тре­буе­мое зна­че­ние ази­му­та. Тре­ние в под­шип­ни­ках не­зна­чи­тель­но, по­это­му ось вра­ще­ния ро­то­ра со­хра­ня­ет за­дан­ное по­ло­же­ние в про­стран­ст­ве. Поль­зу­ясь стрел­кой, скре­п­лён­ной с ос­но­ва­ни­ем, по шка­ле ази­му­та мож­но кон­тро­ли­ро­вать по­во­рот са­мо­лё­та.

Ги­ро­го­ри­зонт, или ис­кусств. го­ри­зонт, по­зво­ляю­щий пи­ло­ту под­дер­жи­вать свой са­мо­лёт в го­ри­зон­таль­ном по­ло­же­нии, ко­гда ес­теств. го­ри­зонт не ви­ден, ос­но­ван на ис­поль­зо­ва­нии Г. с вер­ти­каль­ной осью вра­ще­ния, со­хра­няю­щей своё на­прав­ле­ние при на­кло­нах са­мо­лё­та. В ав­то­пи­ло­тах при­ме­ня­ют­ся два Г. с го­ри­зон­таль­ной и вер­ти­каль­ной ося­ми вра­ще­ния; пер­вый слу­жит для со­хра­не­ния кур­са са­мо­лё­та и управ­ля­ет вер­ти­каль­ны­ми ру­ля­ми, вто­рой – для со­хра­не­ния го­ри­зон­таль­но­го по­ло­же­ния са­мо­лё­та и управ­ля­ет го­ри­зон­таль­ны­ми ру­ля­ми.

С по­мо­щью Г. соз­да­ны ав­то­ном­ные инер­ци­аль­ные на­ви­га­ци­он­ные сис­те­мы (ИНС), пред­на­зна­чен­ные для оп­ре­де­ле­ния ко­ор­ди­нат, ско­ро­сти и ори­ен­та­ции под­виж­но­го объ­ек­та (ко­раб­ля, са­мо­лёта, кос­мич. ап­па­ра­та и т. п.) без ис­поль­зо­ва­ния к.-л. внеш­ней ин­фор­ма­ции. В со­став ИНС кро­ме Г. вхо­дят ак­се­ле­ро­мет­ры, пред­на­зна­чен­ные для из­ме­ре­ния ус­ко­ре­ния (пе­ре­груз­ки) объ­ек­та, а так­же ком­пь­ю­тер, ин­тег­ри­рую­щий по вре­ме­ни вы­ход­ные сиг­на­лы ак­се­ле­ро­мет­ров и вы­даю­щий на­ви­га­ци­он­ную ин­фор­ма­цию с учё­том по­ка­за­ния Г. К нач. 21 в. соз­да­ны на­столь­ко точ­ные ИНС, что даль­ней­ше­го по­вы­ше­ния точ­но­стей для ре­ше­ния мн. за­дач уже не тре­бу­ет­ся.

Раз­ви­тие ги­ро­ско­пич. тех­ни­ки по­след­них де­ся­ти­ле­тий со­сре­до­то­чи­лось на по­ис­ке не­тра­диц. об­лас­тей при­ме­не­ния ги­ро­ско­пич. при­бо­ров – раз­вед­ка по­лез­ных ис­ко­пае­мых, пред­ска­за­ние зем­ле­тря­се­ний, сверх­точ­ное из­ме­ре­ние ко­ор­ди­нат ж.-д. пу­тей и неф­те­про­во­дов, мед. тех­ни­ка и мн. дру­гое.

Неклассические виды гироскопов

Вы­со­кие тре­бо­ва­ния к точ­но­сти и экс­плу­та­ци­он­ным ха­рак­те­ри­сти­кам ги­ро­ско­пич. при­бо­ров при­ве­ли не толь­ко к даль­ней­шим усо­вер­шен­ст­во­ва­ни­ям клас­сич. Г. с вра­щаю­щим­ся ро­то­ром, но и к по­ис­кам прин­ци­пи­аль­но но­вых идей, по­зво­ляю­щих ре­шить про­бле­му соз­да­ния чув­ст­вит. дат­чи­ков для ин­ди­ка­ции и из­ме­ре­ния уг­ло­вых дви­же­ний объ­ек­та в про­стран­ст­ве. Это­му спо­соб­ст­во­ва­ли ус­пе­хи кван­то­вой элек­тро­ни­ки, ядер­ной фи­зи­ки и др. об­лас­тей точ­ных на­ук.

В ги­ро­ско­пе с воз­душ­ной опо­рой ша­ри­ко­вые под­шип­ни­ки, ис­поль­зуе­мые в тра­диц. кар­да­но­вом под­ве­се, за­ме­не­ны «га­зо­вой по­душ­кой» (га­зо­ди­на­мич. опо­рой). Это пол­но­стью уст­ра­ни­ло из­нос ма­те­риа­ла опор во вре­мя ра­бо­ты и по­зво­ли­ло поч­ти не­ог­ра­ни­чен­но уве­ли­чить вре­мя служ­бы при­бо­ра. К не­дос­тат­кам га­зо­вых опор от­но­сят­ся до­воль­но боль­шие по­те­ри энер­гии и воз­мож­ность вне­зап­но­го от­ка­за при слу­чай­ном кон­так­те ро­то­ра с по­верх­но­стью опо­ры.

По­плав­ко­вый ги­ро­скоп пред­став­ля­ет со­бой ро­тор­ный Г., в ко­то­ром для раз­груз­ки под­шип­ни­ков под­ве­са все под­виж­ные эле­мен­ты взве­ши­ва­ют­ся в жид­ко­сти с боль­шой плот­но­стью так, что­бы вес ро­то­ра вме­сте с ко­жу­хом урав­но­ве­ши­вал­ся гид­ро­ста­тич. си­ла­ми. Бла­го­да­ря это­му на мно­го по­ряд­ков сни­жа­ет­ся су­хое тре­ние в осях под­ве­са и уве­ли­чи­ва­ет­ся удар­ная и виб­рац. стой­кость при­бо­ра. Гер­ме­тич­ный ко­жух, вы­пол­няю­щий роль внутр. рам­ки кар­да­но­во­го под­ве­са, на­зы­ва­ет­ся по­плав­ком. Ро­тор Г. внут­ри по­плав­ка вра­ща­ет­ся на возд. по­душ­ке в аэ­ро­ди­на­мич. под­шип­ни­ках со ско­ро­стью по­ряд­ка 30–60 тыс. обо­ро­тов в ми­ну­ту. Для по­вы­ше­ния точ­но­сти при­бо­ра не­об­хо­ди­мо ис­поль­зо­ва­ние сис­те­мы тер­мо­ста­би­ли­за­ции. По­плав­ко­вый Г. с боль­шим вяз­ким тре­ни­ем жид­ко­сти на­зы­ва­ет­ся так­же ин­тег­ри­рую­щим ги­ро­ско­пом.

Рис. 4. Динамически настраиваемый гироскоп с внутренним кардановым подвесом: 1 – ротор; 2 – внутреннее кольцо; 3 и 4 – торсионы; 5 – электродвигатель.

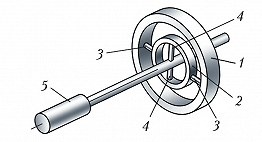
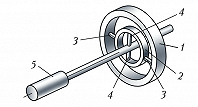
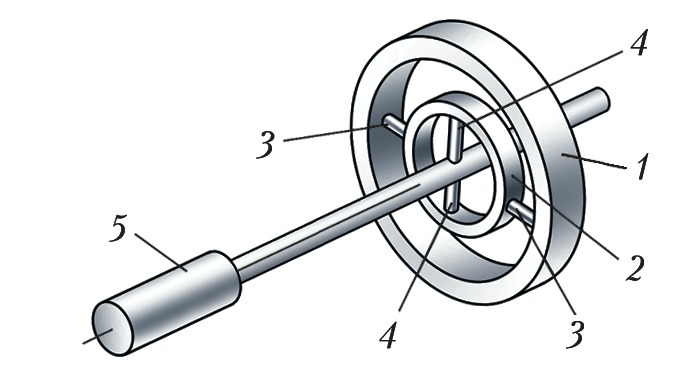
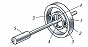
Ди­на­ми­че­ски на­страи­вае­мый ги­ро­скоп (ДНГ) при­над­ле­жит к клас­су Г. с уп­ру­гим под­ве­сом ро­то­ра, в ко­то­рых сво­бо­да уг­ло­вых дви­же­ний оси собств. вра­ще­ния обес­пе­чи­ва­ет­ся за счёт уп­ру­гой по­дат­ли­во­сти кон­ст­рук­тив­ных эле­мен­тов (напр., тор­сио­нов). В ДНГ, в от­ли­чие от клас­сич. Г., ис­поль­зу­ет­ся т. н. внутр. кар­да­нов под­вес (рис. 4), об­ра­зо­ван­ный внутр. коль­цом 2, ко­то­рое из­нут­ри кре­пит­ся тор­сио­на­ми 4 к ва­лу элек­тро­дви­га­те­ля 5, а сна­ру­жи – тор­сио­на­ми 3 к ро­то­ру 1. Мо­мент тре­ния в под­ве­се про­яв­ля­ет­ся толь­ко в ре­зуль­та­те внутр. тре­ния в ма­те­риа­ле уп­ру­гих тор­сио­нов. В ДНГ за счёт под­бо­ра мо­мен­тов инер­ции ра­мок под­ве­са и уг­ло­вой ско­ро­сти вра­ще­ния ро­то­ра осу­ще­ст­в­ля­ет­ся ком­пен­са­ция уп­ру­гих мо­мен­тов под­ве­са, при­ло­жен­ных к ро­то­ру. К дос­то­ин­ст­вам ДНГ от­но­сят­ся их ми­ниа­тюр­ность, от­сут­ст­вие под­шип­ни­ков со спе­ци­фич. мо­мен­та­ми тре­ния, при­сут­ст­вую­щи­ми в клас­сич. кар­да­но­вом под­ве­се, вы­со­кая ста­биль­ность по­ка­за­ний, от­но­си­тель­но не­вы­со­кая стои­мость.

Коль­це­вой ла­зер­ный ги­ро­скоп (КЛГ), на­зы­вае­мый так­же кван­то­вым ги­ро­ско­пом, соз­дан на ос­но­ве ла­зе­ра с коль­це­вым ре­зо­на­то­ром, в ко­то­ром по замк­ну­то­му оп­тич. кон­ту­ру од­но­вре­мен­но рас­про­стра­ня­ют­ся встреч­ные элек­тро­маг­нит­ные вол­ны. К дос­то­ин­ст­вам КЛГ от­но­сят­ся от­сут­ст­вие вра­щаю­ще­го­ся ро­то­ра, под­шип­ни­ков, под­вер­жен­ных дей­ст­вию сил тре­ния, вы­со­кая точ­ность.

Во­ло­кон­но-оп­ти­че­ский ги­ро­скоп (ВОГ) пред­став­ля­ет со­бой во­ло­кон­но-оп­ти­че­ский ин­тер­фе­ро­метр, в ко­то­ром рас­про­стра­ня­ют­ся встреч­ные элек­тро­маг­нит­ные вол­ны. ВОГ яв­ля­ет­ся ана­ло­го­вым пре­об­ра­зо­ва­те­лем уг­ло­вой ско­ро­сти вра­ще­ния ос­но­ва­ния, на ко­то­ром он ус­та­нов­лен, в вы­ход­ной элек­трич. сиг­нал.

Вол­но­вой твер­до­тель­ный ги­ро­скоп (ВТГ) ос­но­ван на ис­поль­зо­ва­нии инерт­ных свойств уп­ру­гих волн в твёр­дом те­ле. Уп­ру­гая вол­на мо­жет рас­про­стра­нять­ся в сплош­ной сре­де, не из­ме­няя сво­ей кон­фи­гу­ра­ции. Ес­ли воз­бу­дить стоя­чие вол­ны уп­ру­гих ко­ле­ба­ний в осе­сим­мет­рич­ном ре­зо­на­то­ре, то вра­ще­ние ос­но­ва­ния, на ко­то­ром ус­та­нов­лен ре­зо­на­тор, вы­зы­ва­ет по­во­рот стоя­чей вол­ны на мень­ший, но из­вест­ный угол. Со­от­вет­ст­вую­щее дви­же­ние вол­ны как це­ло­го на­зы­ва­ет­ся пре­цес­си­ей. Ско­рость пре­цес­сии стоя­чей вол­ны про­пор­цио­наль­на про­ек­ции уг­ло­вой ско­ро­сти вра­ще­ния ос­но­ва­ния на ось сим­мет­рии ре­зо­на­то­ра. К дос­то­ин­ст­вам ВТГ от­но­сят­ся: вы­со­кое от­но­ше­ние точ­ность/це­на; спо­соб­ность пе­ре­но­сить боль­шие пе­ре­груз­ки, ком­пакт­ность и не­боль­шая мас­са, низ­кая энер­го­ём­кость, ма­лое вре­мя го­тов­но­сти, сла­бая за­ви­си­мость от темп-ры ок­ру­жаю­щей сре­ды.

Виб­ра­ци­он­ный ги­ро­скоп (ВГ) ос­но­ван на свой­ст­ве ка­мер­то­на со­хра­нять плос­кость ко­ле­ба­ний сво­их но­жек. В нож­ке ко­леб­лю­ще­го­ся ка­мер­то­на, ус­та­нов­лен­но­го на плат­фор­ме, вра­щаю­щей­ся во­круг оси сим­мет­рии ка­мер­то­на, воз­ни­ка­ет пе­рио­дич. мо­мент сил, час­то­та ко­то­ро­го рав­на час­то­те ко­ле­ба­ния но­жек, а ам­пли­ту­да про­пор­цио­наль­на уг­ло­вой ско­ро­сти вра­ще­ния плат­фор­мы. По­это­му, из­ме­ряя ам­пли­ту­ду уг­ла за­крут­ки нож­ки ка­мер­то­на, мож­но су­дить об уг­ло­вой ско­ро­сти плат­фор­мы. К не­дос­тат­кам ВГ от­но­сит­ся не­ста­биль­ность по­ка­за­ний из-за слож­но­стей вы­со­ко­точ­но­го из­ме­ре­ния ам­пли­ту­ды ко­ле­ба­ний но­жек, а так­же то, что они не ра­бо­та­ют в ус­ло­ви­ях виб­ра­ции, ко­то­рая прак­ти­че­ски все­гда со­про­во­ж­да­ет мес­та ус­та­нов­ки при­бо­ров на дви­жу­щих­ся объ­ек­тах. Идея ка­мер­тон­но­го Г. сти­му­ли­ро­ва­ла це­лое на­прав­ле­ние по­ис­ков но­вых ти­пов Г., ис­поль­зую­щих пье­зо­элек­трич. эф­фект ли­бо виб­ра­цию жид­ко­стей или га­зов в спе­ци­аль­но изо­гну­тых труб­ках и т. п.

Мик­ро­ме­ха­ни­че­ский ги­ро­скоп (ММГ) от­но­сит­ся к Г. низ­ких точ­но­стей (ни­же 10^–1 °/ч). Эта об­ласть тра­ди­ци­он­но счи­та­лась ма­ло­пер­спек­тив­ной для за­дач управ­ле­ния дви­жу­щи­ми­ся объ­ек­та­ми и на­ви­га­ции. Но в кон. 20 в. раз­ра­бот­ка ММГ ста­ла од­ним из наи­бо­лее ин­тен­сив­но раз­ра­ба­ты­вае­мых на­прав­ле­ний ги­ро­ско­пич. тех­ни­ки, тес­но свя­зан­ным с совр. крем­ние­вы­ми тех­но­ло­гия­ми. ММГ пред­став­ля­ет со­бой свое­об­раз­ный элек­трон­ный чип с квар­це­вой под­лож­кой пло­ща­дью в неск. квад­рат­ных мил­ли­мет­ров, на ко­то­рую ме­то­дом фо­то­ли­то­гра­фии на­но­сит­ся пло­ский виб­ра­тор ти­па ка­мер­то­на. Точ­ность совр. ММГ не­ве­ли­ка и дос­ти­га­ет 10¹–10² °/ч, од­на­ко ре­шаю­щее зна­че­ние име­ет ис­клю­чи­тель­но низ­кая стои­мость мик­ро­ме­ха­нич. чув­ст­вит. эле­мен­тов. Бла­го­да­ря ис­поль­зо­ва­нию хо­ро­шо от­ра­бо­тан­ных совр. тех­но­ло­гий мас­со­во­го про­из­вод­ст­ва мик­ро­элек­тро­ни­ки от­кры­ва­ет­ся воз­мож­ность при­ме­не­ния ММГ в со­вер­шен­но но­вых об­лас­тях: ав­то­мо­би­ли и би­нок­ли, те­ле­ско­пы и ви­део­ка­ме­ры, мы­ши и джой­сти­ки пер­со­наль­ных ком­пь­ю­те­ров, мо­биль­ные ро­бо­то­тех­нич. уст­рой­ст­ва и да­же дет­ские иг­руш­ки.

Не­кон­такт­ный ги­ро­скоп от­но­сит­ся к ги­ро­ско­пич. уст­рой­ст­вам сверх­вы­со­ких точ­но­стей (10^–6–5· 10^–4 H /ч). Раз­ра­бот­ка Г. с не­кон­такт­ны­ми под­ве­са­ми на­ча­лась в сер. 20 в. В не­кон­такт­ных под­ве­сах реа­ли­зу­ет­ся со­стоя­ние ле­ви­та­ции, т. е. со­стоя­ние, при ко­то­ром ро­тор Г. «па­рит» в си­ло­вом по­ле под­ве­са без к.-л. ме­ха­нич. кон­так­та с ок­ру­жаю­щи­ми те­ла­ми. Сре­ди не­кон­такт­ных Г. вы­де­ля­ют Г. с элек­тро­ста­тич., маг­нит­ным и крио­ген­ным под­ве­са­ми ро­то­ра. В элек­тро­ста­тич. Г. про­во­дя­щий бе­рил­лие­вый сфе­рич. ро­тор под­ве­шен в ва­куу­ми­ро­ван­ной по­лос­ти в ре­гу­ли­руе­мом элек­трич. по­ле, соз­да­вае­мом сис­те­мой элек­тро­дов. В крио­ген­ном Г. сверх­про­во­дя­щий нио­бие­вый сфе­рич. ро­тор под­ве­шен в маг­нит­ном по­ле; ра­бо­чий объ­ём Г. ох­ла­ж­да­ет­ся до сверх­низ­ких темп-р, так, что­бы ро­тор пе­ре­шёл в сверх­про­во­дя­щее со­стоя­ние. Г. с маг­ни­то­ре­зо­нанс­ным под­ве­сом ро­то­ра яв­ля­ет­ся ана­ло­гом Г. с элек­тро­ста­тич. под­ве­сом ро­то­ра, в ко­то­ром элек­трич. по­ле за­ме­не­но маг­нит­ным, а бе­рил­лие­вый ро­тор – фер­ри­то­вым. Совр. Г. с не­кон­такт­ны­ми под­ве­са­ми – это слож­ней­шие при­бо­ры, ко­то­рые во­бра­ли в се­бя но­вей­шие дос­ти­же­ния тех­ни­ки.

Кро­ме пе­ре­чис­лен­ных вы­ше ти­пов Г. про­во­ди­лись и про­во­дят­ся ра­бо­ты над эк­зо­тич. ти­па­ми Г., та­ки­ми, как ион­ный Г., ядер­ный ги­ро­скоп и др.

Математические задачи в теории гироскопа

Ма­те­ма­тич. ос­но­вы тео­рии Г. за­ло­же­ны Л. Эй­ле­ром в 1765 в его ра­бо­те «Theoria motus corporum solidorum sue rigidorum». Дви­же­ние клас­си­че­ско­го Г. опи­сы­ва­ет­ся сис­те­мой диф­фе­рен­ци­аль­ных урав­не­ний 6-го по­ряд­ка, ре­ше­ние ко­то­рой ста­ло од­ной из са­мых зна­ме­ни­тых ма­те­ма­тич. за­дач. Эта за­да­ча от­но­сит­ся к раз­де­лу тео­рии вра­ща­тель­но­го дви­же­ния твёр­до­го те­ла и яв­ля­ет­ся обоб­ще­ни­ем за­дач, ре­шае­мых до кон­ца про­сты­ми сред­ст­ва­ми клас­сич. ана­ли­за. Од­на­ко при этом она на­столь­ко труд­на, что ещё да­ле­ка от за­вер­ше­ния, не­смот­ря на ре­зуль­та­ты, по­лу­чен­ные круп­ней­ши­ми ма­те­ма­ти­ка­ми 18–20 вв. Совр. ги­ро­ско­пич. при­бо­ры по­тре­бо­ва­ли ре­ше­ния но­вых ма­те­ма­тич. за­дач. Дви­же­ние не­кон­такт­ных Г. с вы­со­кой точ­но­стью под­чи­ня­ет­ся за­ко­нам ме­ха­ни­ки, по­это­му, ре­шая урав­не­ния дви­же­ния Г. с по­мо­щью ком­пь­ю­те­ра, мож­но точ­но пред­ска­зы­вать по­ло­же­ние оси Г. в про­стран­ст­ве. Бла­го­да­ря это­му раз­ра­бот­чи­кам не­кон­такт­ных Г. не при­хо­дит­ся ба­лан­си­ро­вать ро­тор с точ­но­стью 10^–10 м, ко­то­рую не­воз­мож­но дос­тичь при совр. уров­не тех­но­ло­гии. Дос­та­точ­но точ­но из­ме­рять по­греш­но­сти из­го­тов­ле­ния ро­то­ра дан­но­го Г. и вво­дить со­от­вет­ст­вую­щие по­прав­ки в про­грам­мы об­ра­бот­ки сиг­на­лов Г. По­лу­чаю­щие­ся с учё­том этих по­пра­вок урав­не­ния дви­же­ния Г. ока­зы­ва­ют­ся очень слож­ны­ми, и для их ре­ше­ния при­хо­дит­ся при­ме­нять весь­ма мощ­ные ком­пью­те­ры, ис­поль­зую­щие ал­го­рит­мы, ос­но­ван­ные на по­след­них дос­ти­же­ни­ях ма­те­ма­ти­ки. Раз­ра­бот­ка про­грамм рас­чё­та дви­же­ния Г. с не­кон­такт­ны­ми под­ве­са­ми по­зво­ля­ет су­ще­ст­вен­но по­вы­сить точ­ность Г., а сле­до­ва­тель­но, и точ­ность оп­ре­де­ле­ния ме­сто­по­ло­же­ния объ­ек­та, на ко­то­ром ус­та­нов­ле­ны эти ги­ро­ско­пы.