КВАЗИО́ПТИКА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
КВАЗИО́ПТИКА (от квази... и оптика), раздел волновой физики, в котором изучается распространение и дифракция локализованных электромагнитных волн, называемых волновыми пучками, поперечные размеры $d$ которых много больше длины волны $\lambda$. Вследствие этого дифракция возникает на расстояниях $d^2/\lambda$, превышающих поперечный размер $d$. Это свойство позволяет при описании дифракции перейти от волнового уравнения для напряжённостей электромагнитного поля к упрощённому параболич. уравнению для комплексной амплитуды. Так, при распространении волнового пучка вдоль оси $z$ его амплитуда $A$ медленно меняется в пространстве согласно параболич. уравнению: $$\frac {\partial A}{\partial z}=- \frac {i \lambda}{4 \pi} \left(\frac {\partial^2A}{\partial x^2}+ \frac {\partial^2A}{\partial y^2} \right). \quad\tag{*}$$В одномерном случае это уравнение аналогично уравнению Шрёдингера для волновой функции в квантовой механике. Параболич. уравнение описывает дифракцию как поперечную диффузию лучевой амплитуды (по Юнгу), в процессе которой меняются профиль интенсивности и форма волнового фронта. Его решение полностью соответствует дифракционной теории Гюйгенса – Френеля. К. занимает промежуточное положение между геометрической оптикой, которая рассматривает изолированные друг от друга лучевые трубки и не учитывает дифракцию, и волновой оптикой, описывающей дифракцию волн с поперечным масштабом порядка длины волны.
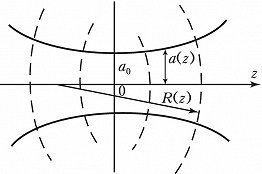
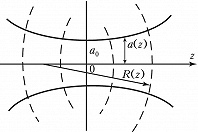
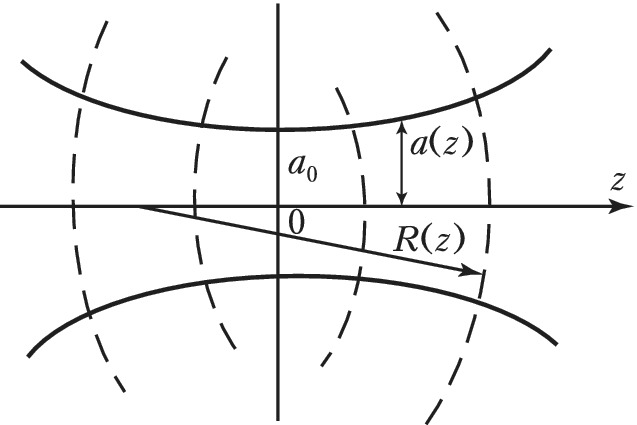
В К. часто используются гауссовы пучки (рис. 1), которые являются важным классом решений уравнения (*). Они обладают автомодельными свойствами, т. е. с точностью до масштаба сохраняют свою структуру в разных сечениях $z= \text{const}$: $A=E \psi^{-1} \exp[-(x^2+y^2)/(a^2_0\psi)]$ , где $a_0$ – начальная ширина пучка, $\psi (z)=1-iz/l_d$, $l_d=\pi a_0^2/\lambda$ – дифракционная длина. Ширина пучка увеличивается с расстоянием как $a(z)=a_0(1+z^2/l^2_d)^{1/2}$, а кривизна волнового фронта – по закону $R=z+l_d^2/z$. На дифракционной длине ширина превышает начальный размер в $\sqrt{2}$ раз, а радиус кривизны минимален: $R_{мин}=2l_d$. В дальнем поле $(z \gg l_d)$ формируется расходящаяся волна с угловой расходимостью $\theta_d=a/z=\lambda/(\pi a_0)$. Так как $\theta_d \ll 1$, волновой пучок называют также параксиальным. Гауссов пучок предельно малой ширины $(a_0 \to 0)$ переходит в функцию точечного источника параболич. уравнения.
Метод параболич. уравнения впервые (1944) развил М. А. Леонтович при исследовании задачи о распространении радиоволн вдоль неоднородной и неровной поглощающей поверхности Земли. Этот метод стали применять при анализе распространения миллиметровых волн в квазиоптич. устройствах, в частности в открытых передающих трактах – линзовых и зеркальных линиях. Он оказался незаменимым в теории открытых резонаторов, широко применяющихся в лазерах, и при описании распространения волн в диэлектрич. волноводах, используемых в волоконной оптике.
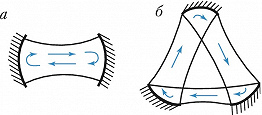
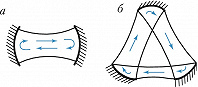
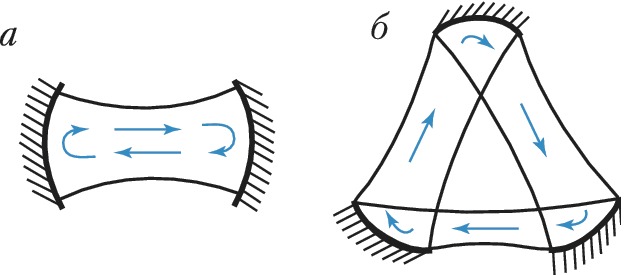
Открытый резонатор в простом варианте представляет собой систему двух параллельных зеркал, расположенных друг напротив друга (рис. 2). Лучшую локализацию обеспечивают вогнутые зеркала. Осн. пространственной модой такого резонатора является гауссов пучок. Открытые резонаторы обладают дискретным спектром собственных частот, поэтому они оказались удобной резонансной системой не только для лазеров, но и для др. квазиоптич. устройств оптич. и субмиллиметрового диапазонов.
Методы К. используются и в слабонеоднородных средах, в которых показатель преломления $n$ незначительно меняется в пространстве: $n=n_0+\delta n(x,y,z)$, $|\delta n| \ll n_0$. Вариации $\delta n$ могут быть регулярными и случайными. В зависимости от вида неоднородности реализуются разл. режимы распространения. В градиентном волноводе с параболич. профилем $\delta n=-n_0(x^2+y^2)/h^2$ осн. поперечная мода имеет плоский волновой фронт и гауссово распределение амплитуды шириной $a_{00} \cong \sqrt{\lambda h}$ ($h$ – эффективная толщина волновода). Поскольку $h/a_{00} \approx a_{00}/ \lambda \gg 1$, мода локализуется вблизи оси волновода. Отрезок градиентного волновода обладает фокусирующими свойствами. В линейном неоднородном слое с профилем $\delta n=n_0x/h$ пучок отклоняется в сторону бóльших значений показателя преломления. В случае периодич. модуляции показателя преломления, напр. по гармонич. закону $\delta n \sim \cos(2 \pi x/h)$, возникает дифракция в тонких или толстых слоях. Так рассматривается, напр., распространение волн в фотонных кристаллах, дискретных волноводах, акустооптич. модуляторах.
В слабо нелинейных средах К. позволяет описать самовоздействие и взаимодействие волновых пучков на основе решения нелинейного уравнения Шрёдингера. С помощью этого уравнения описываются солитоны, самофокусировка света и дефокусировка, дифракция на индуцированных решётках, обращение волнового фронта и др.
По аналогии с волновыми пучками в К. вводится понятие волновых пакетов – волн с медленной модуляцией амплитуды и фазы во времени. Поведение огибающей волнового пакета также описывается параболич. уравнением, которое учитывает дисперсию групповой скорости. Волновой пакет с гауссовой огибающей испытывает дисперсионное расплывание, сохраняя свою форму.
Методы К. оказались пригодными для волн любой природы и в любом диапазоне длин волн, если выполнен необходимый критерий применимости: $d \gg \lambda$.