ОТКРЫ́ТЫЙ РЕЗОНА́ТОР

ОТКРЫ́ТЫЙ РЕЗОНА́ТОР, ко­ле­ба­тель­ная сис­те­ма, со­стоя­щая из зер­кал, удер­жи­ваю­щих пу­тём мно­го­крат­ных от­ра­же­ний сла­бо за­ту­хаю­щие элек­тро­маг­нит­ные ко­ле­ба­ния в ог­ра­ни­чен­ном объ­ё­ме про­стран­ст­ва. О. р. ис­поль­зу­ет­ся в ла­зе­рах, па­ра­мет­рич. ге­не­ра­то­рах све­та, ин­тер­фе­ро­мет­рах, оро­тро­нах, ли­ни­ях за­держ­ки и др. В оп­ти­ке О. р. обыч­но на­зы­ва­ют оп­ти­че­ским ре­зо­на­то­ром

. О. р. пред­ло­жил в 1958 А. М. Про­хо­ров

 >>

, по­сколь­ку в оп­тич. диа­па­зо­не по­стро­ить объ­ём­ный ре­зо­на­тор

 >>

за­труд­ни­тель­но из-за ма­ло­сти раз­ме­ров и боль­ших по­терь энер­гии на стен­ках.

Наи­бо­лее ши­ро­ко при­ме­ня­ют­ся двух­зер­каль­ные О. р. Ра­диу­сы кри­виз­ны зер­кал $R_1$ и $R_2$ и рас­стоя­ние ме­ж­ду ни­ми $d$ вы­би­ра­ют­ся та­ки­ми, что­бы эле­мен­тар­ные лу­чи по­сле мно­го­крат­ных от­ра­же­ний об­ра­зо­вы­ва­ли кау­сти­че­скую по­верх­ность и не ухо­ди­ли в сво­бод­ное про­стран­ст­во. Ус­той­чи­вые рас­пре­де­ле­ния по­ля внут­ри О. р. пред­став­ля­ют со­бой про­доль­ные и по­пе­реч­ные мо­ды. Они ха­рак­те­ри­зу­ют­ся тре­мя ин­дек­са­ми: $q$, $m$, $n$. Ин­декс про­доль­ных мод ука­зы­ва­ет, сколь­ко по­лу­волн ук­ла­ды­ва­ет­ся ме­ж­ду зер­ка­ла­ми: $q=2d/\lambda=1,2,3,\dots$ ($\lambda$ – дли­на вол­ны). Раз­ре­же­ние спек­тра соб­ст­вен­ных час­тот О. р. по про­доль­но­му ин­дек­су $q$ дос­ти­га­ют при­ме­няя свя­зан­ные ре­зо­на­то­ры или спец. оп­тич. фильт­ры. Су­ще­ст­ву­ют так­же разл. ме­то­ды раз­ре­же­ния спек­тра, ос­но­ван­ные на при­ме­не­нии линз, диа­фрагм, про­фи­ли­ро­ван­ных зер­кал и др. По­пе­реч­ные мо­ды опи­сы­ва­ют рас­пре­де­ле­ние ам­пли­ту­ды и фа­зы в се­че­нии пуч­ка. Ин­дек­сы $m$ и $n$ по­ка­зы­ва­ют чис­ло ну­лей ам­пли­ту­ды ко­ле­ба­ний по двум по­пе­реч­ным ко­ор­ди­на­там.

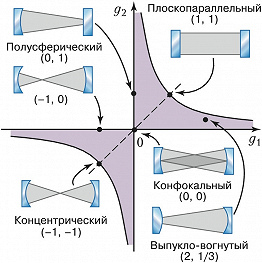
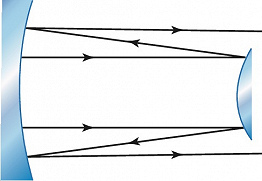
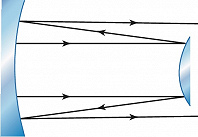
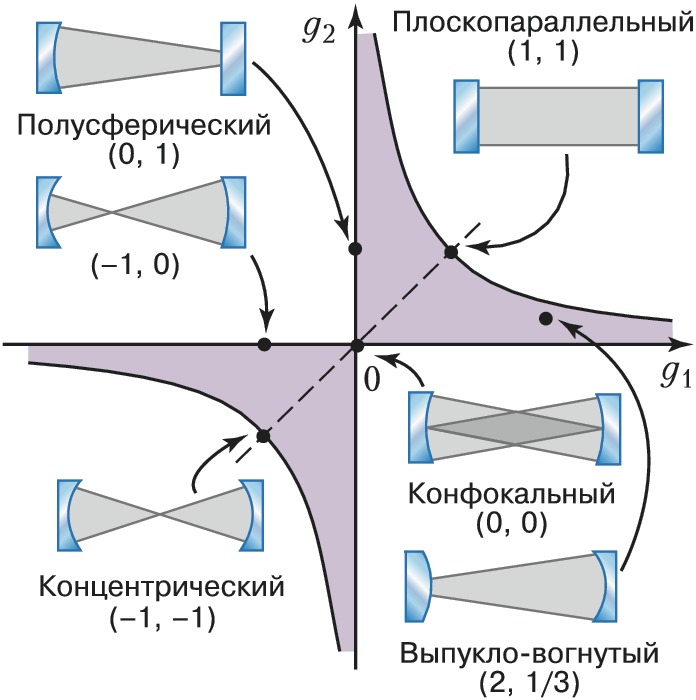
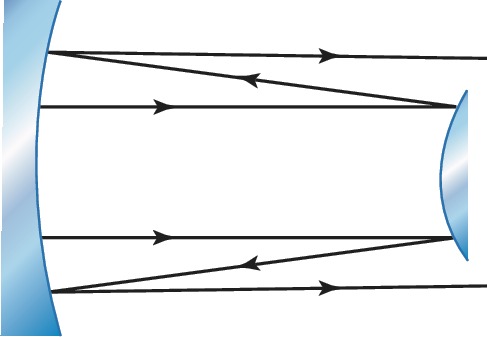
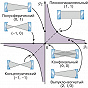
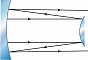
Ус­той­чи­вые мо­ды су­ще­ст­ву­ют лишь в об­лас­ти зна­че­ний па­ра­мет­ров, оп­ре­де­ляе­мой не­ра­вен­ст­ва­ми 

$$0 \leq (1-d/R_1)(1-d/R_2) \geq 1.$$ Ра­диу­сы кри­виз­ны счи­та­ют­ся по­ло­жи­тель­ны­ми для во­гну­тых зер­кал и от­ри­ца­тель­ны­ми для вы­пук­лых. На рис. 1 пред­став­ле­ны осн. ти­пы ус­той­чи­вых О. р. Плос­ко­па­рал­лель­ные О. р. с $R_1=R_2=\infty$ ис­поль­зу­ются в ин­тер­фе­ро­мет­рах и по­лу­про­водни­ко­вых ла­зе­рах. В кон­фо­каль­ных О. р. с $R_1=R_2=d$ дос­ти­га­ет­ся наи­мень­ший диа­метр пуч­ка для за­дан­ной дли­ны ре­зо­на­то­ра. В кон­цен­три­че­ских О. р. с $R_1=R_2=d/2$ пе­ре­тяж­ка пуч­ка рас­по­ло­же­на в цен­тре ре­зо­на­то­ра. У по­лу­сфе­ри­че­ско­го О. р. ра­ди­ус кри­виз­ны од­но­го из зер­кал ра­вен дли­не ре­зо­на­то­ра: $R_2=d$, $R_1=\infty$. В вы­пук­ло-во­гну­том О. р. с $R_1R_2 \lt 0$ пе­ре­тяж­ка пуч­ка, где по­ле мак­си­маль­но, рас­по­ло­же­на вне ре­зо­на­то­ра. Это свой­ст­во ис­поль­зу­ет­ся в мощ­ных ла­зе­рах. В них ино­гда при­ме­ня­ют­ся не­ус­той­чи­вые О. р., со­стоя­щие из ма­ло­го вы­пук­ло­го и боль­шо­го во­гну­то­го зер­кал (рис. 2). Вы­ход­ное из­лу­че­ние в этом слу­чае при­об­ре­та­ет фор­му труб­ча­то­го пуч­ка.

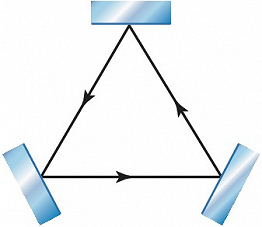
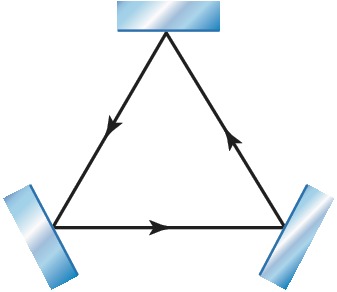
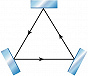
Ино­гда ис­поль­зу­ют­ся так­же трёх­зер­каль­ные О. р. (рис. 3). С их по­мо­щью соз­да­ют­ся коль­це­вые ла­зе­ры и ла­зер­ные ги­ро­ско­пы, ко­то­рые ис­поль­зу­ют эф­фект Сань­я­ка – по­яв­ле­ние фа­зо­во­го сдви­га встреч­ных све­то­вых волн во вра­щаю­щем­ся коль­це­вом ин­тер­фе­ро­мет­ре.

Доб­рот­ность ко­ле­ба­ний в О. р. за­ви­сит от по­терь энер­гии. Часть из­лу­че­ния вы­хо­дит из О. р. че­рез час­тич­но про­зрач­ное зер­ка­ло в сво­бод­ное про­стран­ст­во, часть энер­гии вол­но­во­го пуч­ка про­хо­дит ми­мо зер­ка­ла из-за ди­фрак­ции на его кра­ях. Та­кие ди­фрак­ци­он­ные по­те­ри тем вы­ше, чем боль­ше по­пе­реч­ные ин­дек­сы $m$ и $n$. Не­ко­то­рая часть из­лу­че­ния по­гло­ща­ет­ся на зер­ка­лах и в объ­ё­ме от­кры­то­го ре­зо­на­то­ра.

Все муз. ин­ст­ру­мен­ты и ряд аку­стич. и ра­дио­тех­нич. при­бо­ров (ре­зо­на­тор Гельм­голь­ца, ка­мер­тон, ан­тен­ные виб­ра­то­ры и др.) по прин­ци­пу дей­ст­вия пред­став­ля­ют со­бой О. р. Од­на­ко из­лу­че­ние этих уст­ройств су­ще­ст­вен­но не влия­ет на спектр их соб­ст­вен­ных час­тот, в то вре­мя как из­лу­че­ние выс­ших мод О. р. с зер­ка­ла­ми яв­ля­ет­ся осн. при­чи­ной раз­ре­же­ния спек­тра.