ОБЪЁМНЫЙ РЕЗОНА́ТОР

ОБЪЁМНЫЙ РЕЗОНА́ТОР элек­тро­маг­нит­ный, замк­ну­тая по­лость с от­ра­жаю­щи­ми стен­ка­ми, внут­ри ко­то­рой мо­гут со­вер­шать­ся сво­бод­ные элек­тро­маг­нит­ные ко­ле­ба­ния. Ана­ло­ги­чен ко­ле­ба­тель­но­му кон­ту­ру

и слу­жит для на­ко­п­ле­ния энер­гии за счёт ре­зо­нан­са. Наи­бо­лее час­то ис­поль­зу­ют О. р. пря­мо­уголь­ной, ци­лин­д­рич., сфе­рич. и то­рои­даль­ной форм. Пе­ри­од собств. ко­ле­ба­ний $Т=2π/ω$ ($ω$ – собств. кру­го­вая час­то­та) не пре­вы­ша­ет вре­ме­ни про­хо­ж­де­ния вол­ны ме­ж­ду наи­бо­лее уда­лён­ны­ми стен­ка­ми О. р.: $T$ ($l$– рас­стоя­ние ме­ж­ду стен­ка­ми, $с$ – ско­рость све­та). По­это­му в длин­но­вол­но­вом диа­па­зо­не О. р. ока­зы­ва­ют­ся слиш­ком гро­мозд­ки­ми ($l$по­ряд­ка дли­ны вол­ны $λ=cT$) и их при­ме­не­ние тех­ни­че­ски оп­рав­да­но толь­ко в СВЧ-диа­па­зо­не.

В ка­че­ст­ве О. р. мож­но ис­поль­зо­вать от­рез­ки по­лых ме­тал­ли­че­ских вол­но­во­дов

, за­кры­тые на тор­цах ме­тал­лич. пло­с­ки­ми крыш­ка­ми. Внут­ри та­ких О. р. собств. ко­ле­ба­ния мо­гут об­ра­зовы­вать трёх­мер­ные стоя­чие вол­ны двух ти­пов: мо­ды $Е$ (или $ТМ$) с про­доль­ной ком­по­нен­той элек­трич. по­ля $E_z$ и мо­ды $Н$ (или $ТЕ$) с осе­вой ком­по­нен­той маг­нит­но­го по­ля $Н_z$ (рис. 1). Ти­пы ко­ле­ба­ний ха­рак­тери­зу­ют­ся тре­мя ин­дек­са­ми $m$, $n$, $р$, пер­вые два из ко­то­рых от­но­сят­ся к струк­ту­ре по­ля в по­пе­реч­ном се­че­нии, а тре­тий ра­вен чис­лу по­лу­волн, ук­ла­ды­ваю­щих­ся по его дли­не: $p=2l/λ$. Струк­ту­ру по­лей и собств. час­то­ты мож­но рас­счи­тать, ре­шая чис­лен­но или ана­ли­ти­че­ски урав­не­ния Мак­свел­ла при оп­ре­де­лён­ных гра­нич­ных ус­ло­ви­ях на стен­ках. Напр., на по­верх­но­сти иде­аль­но­го про­вод­ни­ка тан­ген­ци­аль­ная ком­по­нен­та элек­трич. по­ля об­ра­ща­ет­ся в нуль.

В пря­мо­уголь­ном ре­зо­на­то­ре со сто­ро­на­ми $a$, $b$, $l$ про­фи­ли мод опи­сы­ва­ют­ся на­бо­ром функ­ций $Е$, $Н∼ exp(±i𝑘_xx±i𝑘_yy±i𝑘_zz)$, где $𝑘_x$, $𝑘_y$, $𝑘_z$ – про­ек­ции вол­но­во­го век­то­ра $\mathbf {𝑘}$ на со­от­вет­ст­вую­щие оси. Под­ста­нов­ка ис­ко­мо­го ре­ше­ния в урав­не­ния Мак­свел­ла и гра­нич­ные ус­ло­вия по­зво­ля­ют най­ти собств. час­то́­ты. Спек­тры $Е$- и $Н$-мод име­ют оди­на­ко­вый вид, хо­тя струк­ту­ра са­мих мод раз­лич­на (про­ис­хо­дит час­тот­ное вы­ро­ж­де­ние): $ω_{mnp}=\pi c \sqrt{m^2/a^2+n^2/b^2+p^2/l^2}.$При этом наи­низ­шей час­то­той собств. ко­ле­ба­ний с $р=0$ яв­ля­ет­ся $ω_{110}$.

В ци­лин­д­рич. ре­зо­на­то­ре радиусом $r_0$с про­доль­ным элек­трическим по­лем собственные час­то́­ты име­ют вид: $ω_{mnp}=c \sqrt {(_{mn}/r_0)^2+(p \pi/l)^2},$где $ν_{mn}$ – $n$-й ко­рень функ­ции Бес­се­ля $m$-го по­ряд­ка. Мо­да в ци­лин­д­рич. ре­зо­на­то­ре с про­доль­ным маг­нит­ным по­лем име­ет собств. час­то­ту $ω_{mnp}=c \sqrt{(\mu_{mn}/r_0)^2+(p \pi/l)^2}$ , где $μ_{mn} – n$-й ко­рень про­из­вод­ной функ­ции Бес­се­ля $m$-го по­ряд­ка. При $l< 2,04r_0$ глав­ным яв­ля­ет­ся ко­ле­ба­ние $E_{010}$ с соб­ственной час­то­той $ω_{010}= 2,04c/r_0$. С рос­том дли­ны ре­зо­на­то­ра при $l>2,04r_0$ осн. мо­дой ста­но­вит­ся $H111$ с час­то­той $ω111=c\sqrt{(1,84/r_0)^2+ \pi^2/l^2}.$

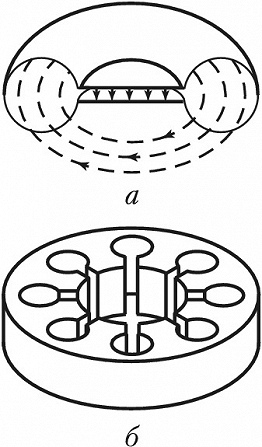
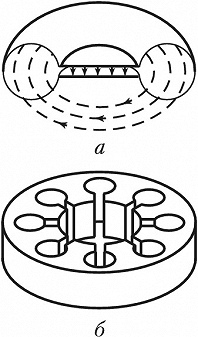
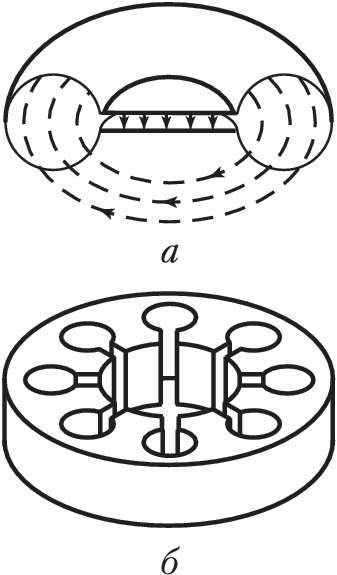
На прак­ти­ке при­ме­ня­ют­ся О. р. то­рои­даль­ной и бо­лее слож­ной форм. То­рои­даль­ный О. р. с ём­ко­ст­ным се­точ­ным за­зо­ром (рис. 2, а) при­ме­ня­ет­ся в ка­че­ст­ве ко­ле­ба­тель­ной сис­те­мы клис­тро­на

. Элек­трич. по­ле ло­ка­ли­зу­ет­ся в ём­ко­ст­ном за­зо­ре, маг­нит­ное – в то­рои­даль­ной по­лос­ти. Элек­тро­ны ус­ко­ря­ют­ся или тор­мо­зят­ся, про­ле­тая се­точ­ный за­зор. В маг­не­тро­нах

 >>

ис­поль­зу­ет­ся коль­це­вая ко­ле­ба­тель­ная сис­те­ма, со­стоя­щая из О. р. в ви­де ци­лин­д­рич. по­лос­тей внут­ри мас­сив­но­го ано­да (рис. 2, б).

О. р. из­го­тав­ли­ва­ют це­ли­ком из ме­тал­лов и их спла­вов с вы­со­кой элек­тро­про­вод­но­стью или по­кры­ва­ют по­лость из­нут­ри сло­ем та­ких ме­тал­лов. О. р. с очень вы­со­кой доб­рот­но­стью по­лу­ча­ют из сверх­про­во­дя­щих ме­тал­лов при низ­ких темп-рах. На­строй­ка О. р. на оп­ре­де­лён­ную час­то­ту про­из­во­дит­ся из­ме­нени­ем его объ­ё­ма пу­тём пе­ре­ме­ще­ния сте­нок или вве­де­ния в по­лость О. р. ме­тал­лич. порш­ней, пла­стин и др. на­стро­еч­ных эле­мен­тов. Связь с внеш­ни­ми элек­трич. це­пя­ми осу­ще­ст­в­ля­ет­ся обыч­но че­рез от­вер­стия в стен­ках О. р. с по­мо­щью пе­тель, шты­рей и др. эле­мен­тов свя­зи.

В О. р. су­ще­ст­ву­ют по­те­ри элек­тро­маг­нит­ной энер­гии из-за то­ков про­во­ди­мо­сти в ме­тал­лич. стен­ках, а так­же за счёт свя­зи с внеш­ни­ми элек­трич. це­пя­ми. От­но­ше­ние энер­гии, за­па­сён­ной в О. р., к сум­мар­ным по­те­рям энер­гии в нём за пе­ри­од ко­ле­ба­ний на­зы­ва­ет­ся доб­рот­но­стью О. р. Чем вы­ше доб­рот­ность, тем луч­ше ка­че­ст­во О. р. Доб­рот­ность О. р. мо­жет дос­ти­гать ве­ли­чин 10⁵ при ком­нат­ных темп-рах и 10⁷ при крио­ген­ных темп-рах.

Кро­ме ме­тал­ли­че­ских при­ме­ня­ют­ся ди­элек­трич. О. р., вы­пол­нен­ные из ди­элек­три­ков с вы­со­кой ди­элек­трич. про­ни­цае­мо­стью. Рас­пре­де­ле­ние по­ля в ди­элек­трич. О. р. близ­ко к рас­пре­де­ле­нию по­ля в ме­тал­лич. по­лых ре­зо­на­то­рах та­кой же фор­мы. В фо­тон­ных кри­стал­лах

мож­но соз­да­вать мик­ро­ре­зо­на­то­ры раз­ме­ром в од­ну ячей­ку пе­рио­дич. струк­ту­ры (по­ряд­ка дли­ны вол­ны). Вы­со­кую доб­рот­ность обес­пе­чи­ва­ет эф­фект пол­но­го от­ра­же­ния от ок­ру­жаю­щих яче­ек в зо­не не­про­зрач­но­сти на оп­ре­де­лён­ных час­то­тах.

О. р. ши­ро­ко ис­поль­зу­ют­ся в тех­ни­ке в ка­че­ст­ве ко­ле­ба­тель­ных сис­тем ге­не­ра­то­ров и уси­ли­те­лей, фильт­ров, эта­ло­нов час­то­ты, из­ме­рит. кон­ту­ров, для ис­сле­до­ва­ния элек­тро­ди­на­мич. свойств разл. ве­ществ. Ме­тал­лич. О. р. при­ме­ня­ют­ся в диа­па­зо­не час­тот 10⁹–10¹¹ Гц. На бо­лее вы­со­ких час­то­тах доб­рот­ность О. р. па­да­ет, ре­зо­нанс­ные свой­ст­ва те­ря­ют­ся. Эти не­дос­тат­ки уст­ра­ня­ют­ся в от­кры­тых ре­зо­на­то­рах

, за­дер­жи­ваю­щих из­лу­че­ние толь­ко в од­ном на­прав­ле­нии с по­мо­щью зер­кал.