МЕТАЛЛИ́ЧЕСКИЙ ВОЛНОВО́Д

Рис. 1. Прямоугольный (а) и круглый (б) волноводы.

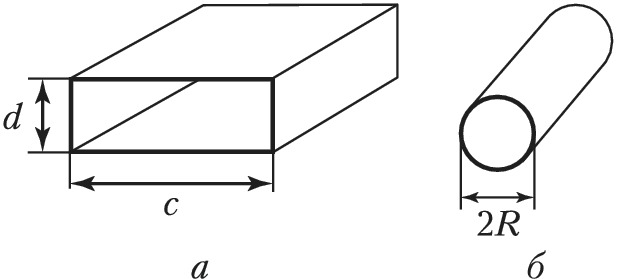
МЕТАЛЛИ́ЧЕСКИЙ ВОЛНОВО́Д, по­лая ме­тал­лич. тру­ба, внут­ри ко­то­рой рас­про­стра­ня­ет­ся элек­тро­маг­нит­ное из­лу­че­ние, ис­пы­ты­ваю­щее мно­го­крат­ное от­ра­же­ние от сте­нок. Обыч­но по­пе­реч­ное се­че­ние М. в. име­ет пря­мо­уголь­ную или круг­лую фор­му (рис. 1). Воз­мож­ность су­ще­ст­во­ва­ния волн внут­ри ме­тал­лич. тру­бы бы­ла тео­ре­ти­че­ски ус­та­нов­ле­на ещё Дж. Рэ­ле­ем в кон. 19 в. Ши­ро­кое раз­ви­тие вол­но­вод­ной тех­ни­ки свя­за­но с ос­вое­ни­ем сан­ти­мет­ро­во­го диа­па­зо­на длин волн для ра­дио­ло­ка­ции в 1930-х гг. Ны­не М. в. при­ме­ня­ют так­же для волн де­ци­мет­ро­во­го и мил­ли­мет­ро­во­го диа­па­зо­нов.

В М. в. мо­гут воз­бу­ж­дать­ся бе­гу­щие вол­ны, раз­ли­чаю­щие­ся час­то­той и струк­ту­рой элек­тро­маг­нит­но­го по­ля (см. Мо­ды), ко­то­рые оп­ре­де­ля­ют­ся ре­ше­ния­ми урав­не­ний Мак­свел­ла с учё­том гра­нич­ных ус­ло­вий на стен­ках вол­но­во­да. В от­ли­чие от по­пе­реч­ных волн в сво­бод­ном про­стран­ст­ве, мо­ды в М. в. обя­за­тель­но име­ют про­доль­ную со­став­ляю­щую элек­три­че­ско­го $E_z$ или маг­нит­но­го $H_z$ по­ля: $E_z=E_{mn}(x,y)\text{exp}[i(ωt-k_zz)]$ – вол­на ТМ-ти­па (от англ. transversal magnetic) или $H_z=H_{mn}(x, y)\text{exp}[i(ωt-k_z)]$ – вол­на ТЕ-ти­па (от англ. transversal electric). (Здесь $E_{mn}$ и $H_{mn}$ – ам­пли­ту­ды со­от­вет­ст­вую­щих волн, $ω$ – уг­ло­вая час­то­та, $t$ – вре­мя, $k_z$ – про­ек­ция вол­но­во­го век­то­ра $\bf{\it{k}}$ на про­доль­ное на­прав­ле­ние $z$.) Це­ло­чис­лен­ные ин­дек­сы $m$ и $n$ для прямо­уголь­но­го М. в. ука­зы­ва­ют чис­ло по­лу­волн, ук­ла­ды­ваю­щих­ся вдоль его сто­рон.

Рис. 2. Структура поля моды Н10 в прямоугольном (а) и Н11 в круглом (б) металлическом волноводе. Сплошными линиями изображены силовые линии электрического поля, штриховыми – магнитного.

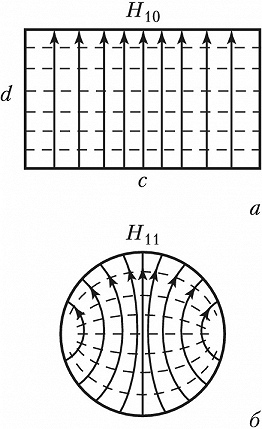
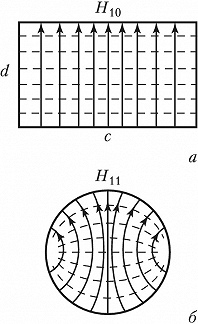
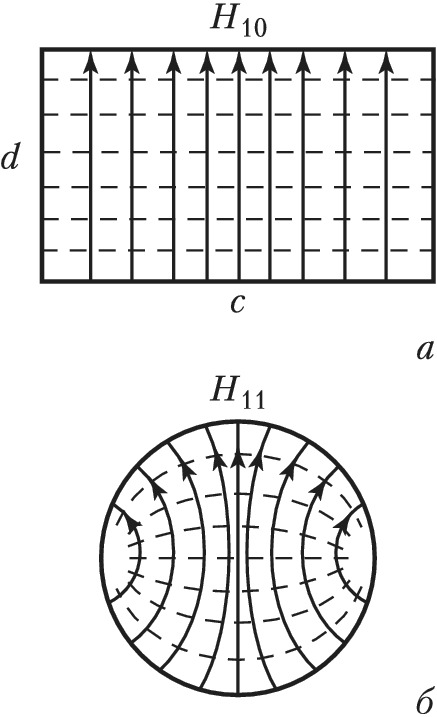
По пря­мо­уголь­но­му вол­но­во­ду с по­пе­реч­ны­ми раз­ме­ра­ми $c$ и $d$ мо­гут рас­про­стра­нять­ся толь­ко вол­ны, дли­на ко­то­рых мень­ше не­ко­то­рой кри­тич. ве­личи­ны $λ_{\text{кр}}=2/\sqrt{(n/c)^2=(m/d)^2}$. Из этой фор­му­лы сле­ду­ет, что один из ин­дек­сов дол­жен быть от­ли­чен от ну­ля и дли­на вол­ны про­хо­дя­ще­го из­лу­че­ния не мо­жет быть боль­ше уд­во­ен­ной ши­ри­ны М. в. Наи­боль­шую кри­тич. дли­ну вол­ны $λ_{\text{кр}}=2c$ име­ет мо­да $H_{10}$ (рис. 2, а), где $c$ – раз­мер ши­ро­кой стен­ки вол­но­во­да. Раз­мер $d$ не влия­ет ни на струк­ту­ру рас­пре­де­ле­ния по­лей, ни на кри­тич. час­то­ту этой мо­ды. Для ТМ-вол­ны низ­шей яв­ля­ет­ся мо­да $E_{11}$.

В М. в. с круг­лым се­че­ни­ем ра­диу­сом $R$ рас­пре­де­ле­ние по­ля опи­сы­ва­ет­ся в по­ляр­ных ко­ор­ди­на­тах $(r, φ)$ функ­ци­ей Бес­се­ля, ум­но­жен­ной на пе­рио­дич. функ­цию уг­ла: $J_n(ν_{nm}r/R)\cos(nφ)$, где $ν_{nm}$ – $m$-й ко­рень функ­ции Бес­се­ля по­ряд­ка $n$ или её про­из­вод­ной. Осн. ти­пом волн в та­ком М. в. яв­ля­ет­ся мо­да $H_{11}$ c наи­боль­шей кри­тич. дли­ной вол­ны $λ_{\text{кр}}=3,41R$ (рис. 2, б), а для волн ТМ-ти­па – мо­да $E_{01}$ с$λ_{\text{кр}}=2,61R$.

Дли­на вол­ны в М. в. $λ=2π/k_z=λ_0/\sqrt{1-(λ_0/λ_\text{кр})^2}$ боль­ше, чем дли­на вол­ны $λ_0$ в сво­бод­ном про­стран­ст­ве. Со­от­вет­ст­вен­но, фа­зо­вая ско­рость $u_\text{ф}$ вол­но­вод­ной мо­ды все­гда боль­ше ско­ро­сти све­та и за­ви­сит от час­то­ты, а груп­по­вая ско­рость $u_\text{гр}$, ха­рак­те­ри­зую­щая ско­рость рас­про­стра­не­ния энер­гии, мень­ше ско­ро­сти све­та. На кри­тич. час­то­те фа­зо­вая ско­рость уст­рем­ля­ет­ся к бес­ко­нечно­сти, а груп­по­вая ско­рость об­ра­ща­ет­ся в нуль – элек­тро­маг­нит­ное из­лу­че­ние не рас­про­стра­ня­ет­ся вдоль М. в. На мень­ших час­то­тах вол­на не мо­жет про­ник­нуть в вол­но­вод.

М. в. ши­ро­ко при­ме­ня­ют­ся в ка­че­ст­ве ли­ний пе­ре­да­чи в разл. уст­рой­ст­вах и при­бо­рах сан­ти­мет­ро­во­го и мил­ли­мет­ро­во­го диа­па­зо­нов длин волн: в ра­дио­ло­ка­ци­он­ных стан­ци­ях для пе­ре­да­чи сиг­на­ла от пе­ре­дат­чи­ка в пе­ре­даю­щую ан­тен­ну и от при­ни­маю­щей ан­тен­ны к при­ём­нику, для удер­жа­ния по­ля в ог­ра­ни­ченном про­стран­ст­ве в СВЧ-уси­ли­те­лях и СВЧ-ге­не­ра­то­рах, для под­во­да энер­гии от маг­не­тро­на в ра­бо­чую ка­ме­ру в мик­ро­вол­но­вой пе­чи и т. п. Для сни­же­ния по­терь внутр. стен­ки М. в. ино­гда по­кры­ва­ют тон­ким сло­ем се­реб­ра на глу­би­ну скин-слоя.