КОЛЕБА́ТЕЛЬНЫЙ КО́НТУР

Рис. 1. Последовательный (а) и параллельный (б) колебательные контуры с источником переменной эдс U=U0cosΩt.

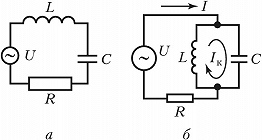
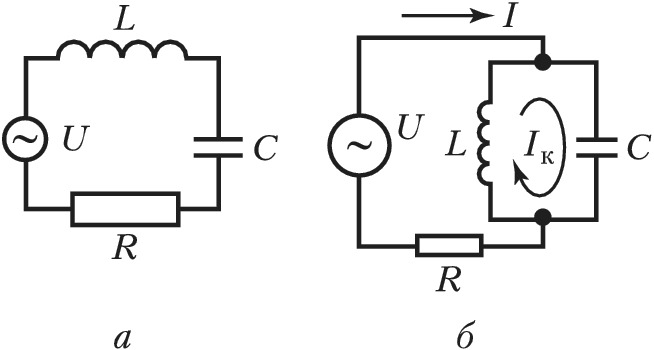
КОЛЕБА́ТЕЛЬНЫЙ КО́НТУР, замк­ну­тая элек­трич. цепь, со­дер­жа­щая ка­туш­ку ин­дук­тив­но­сти и кон­ден­са­тор, в ко­то­рой воз­бу­ж­да­ют­ся собств. ко­ле­ба­ния с час­то­той, оп­ре­де­ляе­мой па­ра­мет­ра­ми це­пи. Схе­мы про­стей­ше­го К. к. при­ве­де­ны на рис. 1 при по­сле­до­ва­тель­ном (а) и па­рал­лель­ном (б) вклю­че­нии внеш­не­го ис­точ­ни­ка пе­ре­мен­ной эдс. При от­сут­ст­вии по­терь (ак­тив­ное со­про­тив­ле­ние $R=0$) и внеш­не­го ге­не­ра­то­ра ($U=0$) в К. к. со­вер­ша­ют­ся гар­мо­нич. ко­ле­ба­ния на­пря­же­ния $V=V_0 \cos \omega_0t$ и то­ка $I=I_0\sin\omega_0t$ с час­то­той $\omega_0=1/ \sqrt {LC}$, где $L$ – ин­дук­тив­ность, $C$ – ём­кость кон­ден­са­то­ра. В К. к. два­ж­ды за пе­ри­од, рав­ный $T_0=2\pi \sqrt{LC}$, про­ис­хо­дит пе­ре­кач­ка энер­гии из элек­трич. по­ля кон­ден­са­то­ра в маг­нит­ное по­ле ка­туш­ки ин­дук­тив­но­сти и об­рат­но. В ре­аль­ных ус­ло­ви­ях за­па­сён­ная энер­гия по­сте­пен­но те­ря­ет­ся из-за на­ли­чия ак­тив­но­го со­про­тив­ле­ния. Ам­пли­ту­да та­ких ко­ле­ба­ний убы­ва­ет по за­ко­ну: $V=V_0e^{-\delta t} \cos \omega t$, где $\delta=R/2L$ – ко­эф. зату­ха­ния, $\omega=\sqrt{\omega_0^2-\delta^2}$ – час­то­та за­тухаю­щих ко­ле­ба­ний. С рос­том $δ$ пе­ри­од ко­ле­ба­ний уве­ли­чи­ва­ет­ся и при $\delta=\omega _0$ об­ра­ща­ет­ся в бес­ко­неч­ность, т. е. дви­же­ние пе­ре­ста­ёт быть пе­рио­ди­че­ским. В це­пи с $δ>ω_0$ ко­ле­ба­ния при раз­ряд­ке кон­ден­са­то­ра не на­блю­да­ют­ся (апе­рио­ди­че­ский про­цесс). Важ­ной ха­рак­те­ри­сти­кой К. к. слу­жит доб­рот­ность $Q=R^{-1}\sqrt{L/C}$.

Ес­ли вклю­чить в К. к. ге­не­ра­тор с пе­ре­мен­ной эдс $U=U_0\cos \Omega t$, то по­сле за­ту­ха­ния собств. ко­ле­ба­ний ус­та­нав­ли­ва­ют­ся вы­ну­ж­ден­ные ко­ле­ба­ния, ста­цио­нар­ная ам­пли­ту­да ко­то­рых оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем$$V_0=\frac{\omega_0^2 U_0}{\sqrt{(\omega_0^2-\Omega^2)^2+4 \delta^2 \Omega^2}}.$$

Рис. 2. Резонансные кривые колебательного контура при добротностях Q1>Q2>Q3.

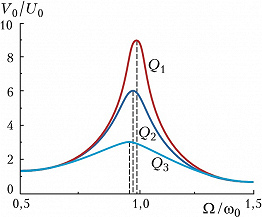
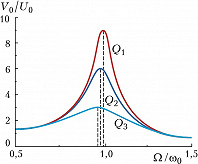
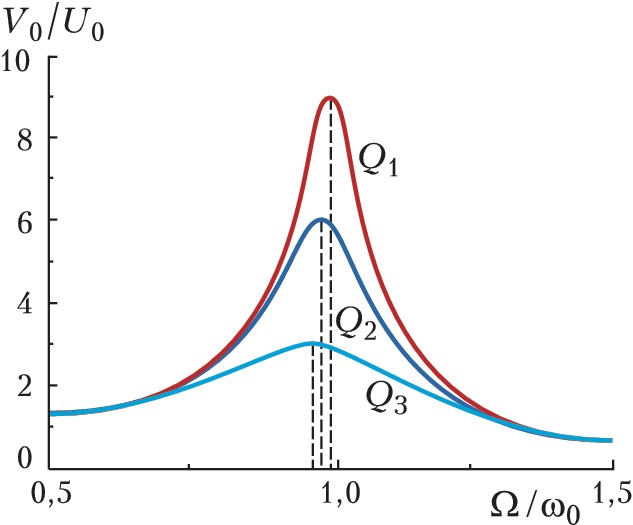
За­ви­си­мость ам­пли­ту­ды ко­ле­ба­ний от час­то­ты $Ω$ внеш­ней эдс (ре­зо­нанс­ная кри­вая) пред­став­ле­на на рис. 2. Чем вы­ше доб­рот­ность, тем ýже и вы­ше ре­зо­нанс­ная кри­вая и тем мень­ше она сме­ща­ет­ся в об­ласть низ­ких час­тот. При ре­зо­нан­се на­пря­же­ний в по­сле­до­ва­тель­ном К. к. ($Ω=ω_0$) ам­пли­ту­да ко­ле­ба­ний $V_{рез}$ в $Q$ раз пре­вы­ша­ет ам­пли­ту­ду внеш­ней эдс $U_0$. При ре­зо­нан­се то­ков в па­рал­лель­ном К. к. ам­пли­ту­да то­ка $I_к$ в кон­ту­ре пре­вы­ша­ет ам­пли­ту­ду то­ка $I$ во внеш­ней це­пи, $I_к=QI.$ Ши­ри­на ре­зо­нанс­ной кри­вой $ΔΩ=ω_0/Q$. Обыч­но $10\lt Q \lt 1000$, по­это­му К. к. по­зво­ля­ет вы­де­лить из мно­же­ст­ва внеш­них сиг­на­лов те, час­то­ты ко­то­рых близ­ки к $ω_0.$ Имен­но это из­бира­тель­ное свой­ст­во К. к. ис­поль­зу­ет­ся на прак­ти­ке.

Кро­ме ли­ней­ных К. к. с по­сто­ян­ны­ми $L$ и $C$, ис­поль­зу­ют­ся не­ли­ней­ные К. к., в ко­то­рых, напр., ём­кость кон­ден­са­то­ра $C $ за­ви­сит от при­ло­жен­но­го на­пря­же­ния. В та­ком К. к. ре­зо­нанс­ная кри­вая име­ет клю­во­об­раз­ную фор­му, т. е. присут­ст­ву­ет об­ласть не­од­но­знач­но­сти, в ко­то­рой на­блю­да­ют­ся скач­ки ам­пли­ту­ды при плав­ном из­ме­не­нии час­то­ты $Ω$ внеш­ней эдс.

К. к. обыч­но при­ме­ня­ют­ся в ка­че­ст­ве ре­зо­нанс­ной сис­те­мы ге­не­ра­то­ров и уси­ли­те­лей в диа­па­зо­не час­тот от 50 кГц до 250 МГц. На бо­лее вы­со­ких час­то­тах роль К. к. иг­ра­ют от­рез­ки двух­про­вод­ных и ко­ак­си­аль­ных ли­ний, а так­же объ­ём­ные ре­зо­на­то­ры. В оп­тич. диа­па­зо­не ре­зо­нанс­ны­ми свой­ст­ва­ми об­ла­да­ют от­кры­тые ре­зо­на­то­ры.