ЗЕ́ЕМАНА ЭФФЕ́КТ

ЗЕ́ЕМАНА ЭФФЕ́КТ, рас­ще­п­ле­ние уров­ней энер­гии, а сле­до­ва­тель­но, и спек­траль­ных ли­ний ато­мов, мо­ле­кул и кри­стал­лов в маг­нит­ном по­ле. З. э. на­блю­да­ет­ся как на спек­траль­ных ли­ни­ях ис­пус­ка­ния, так и на ли­ни­ях по­гло­ще­ния (в этом слу­чае его час­то на­зы­ва­ют об­рат­ным З. э.). Впер­вые об­на­ру­жен в 1896 П. Зее­ма­ном при ис­сле­до­ва­нии спек­тров па­ров на­трия; пер­вую тео­рию на ос­но­ве клас­сич. элек­тро­ди­на­ми­ки раз­ра­бо­тал Х. Ло­ренц (1897), пол­ная тео­рия З. э. соз­да­на на ос­но­ве кван­то­вой ме­ха­ни­ки.

Простой эффект Зеемана: а – спектральная линия частоты ν0, наблюдаемая при отсутствии магнитного поля; б – зеемановский триплет, наблюдаемый в направлении, перпендикулярном напряжённост...

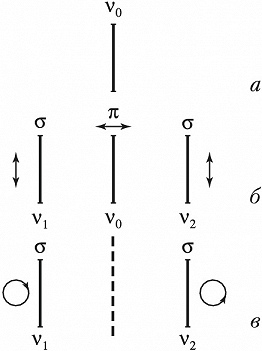
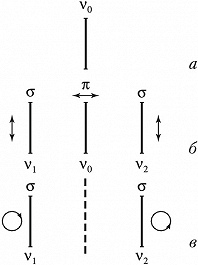
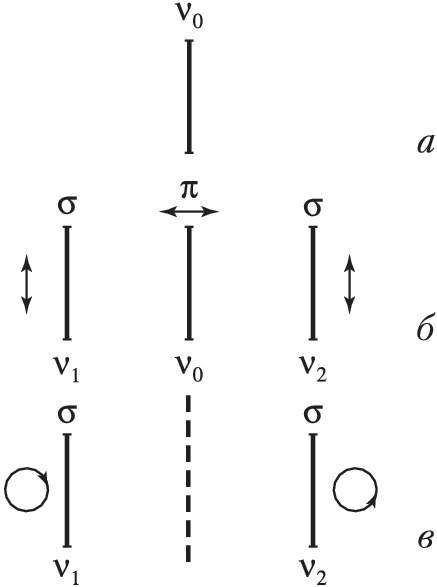
Спек­траль­ная ли­ния в маг­нит­ном по­ле рас­ще­п­ля­ет­ся на неск. по­ля­ри­зо­ван­ных т. н. зее­ма­нов­ских ком­по­нент (зее­ма­нов­ское рас­ще­п­ле­ние), при­чём ха­рак­тер рас­ще­п­ле­ния и по­ля­ри­за­ция ком­по­нент за­ви­сят от на­прав­ле­ния на­блю­де­ния (рис.). В слу­чае т. н. про­сто­го, или нор­маль­но­го, З. э. в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном на­прав­ле­нию на­пря­жён­но­сти маг­нит­но­го по­ля, на­блю­да­ет­ся зее­ма­нов­ский три­плет – три ли­ней­но по­ля­ри­зо­ван­ные ком­по­нен­ты: не­сме­щён­ная от­но­си­тель­но пер­вич­ной ли­нии $π$-ком­по­нен­та, по­ля­ри­зо­ван­ная вдоль по­ля, и две сим­мет­рич­но от неё рас­по­ло­жен­ные $σ$-ком­по­нен­ты, по­ля­ри­зо­ван­ные пер­пен­ди­ку­ляр­но по­лю. При на­блю­де­нии вдоль на­прав­ле­ния на­пря­жён­но­сти маг­нит­но­го по­ля по­лу­ча­ет­ся дуб­лет – две ком­по­нен­ты с кру­го­вой по­ля­ри­за­ци­ей, на­прав­лен­ной в про­ти­во­по­лож­ные сто­ро­ны. Кар­ти­на про­сто­го зее­ма­нов­ско­го рас­щеп­ле­ния на­блю­да­ет­ся для оди­ноч­ных спек­траль­ных ли­ний или в силь­ных маг­нит­ных по­лях (Па­ше­на – Ба­ка эф­фект). В об­щем слу­чае реа­ли­зу­ет­ся слож­ный (ано­маль­ный) З. э.: по­яв­ля­ют­ся груп­пы рав­но­от­стоя­щих ли­ний, при­чём об­щая кар­ти­на сим­мет­рич­на от­но­си­тель­но пер­вич­ной не­сме­щён­ной ли­нии. Чис­ло ком­по­нент слож­но­го З. э. мо­жет дос­ти­гать не­сколь­ких де­сят­ков. Ве­ли­чи­на рас­щеп­ле­ния ма­ла; для маг­нит­ных по­лей с на­пря­жён­но­стью $H$ по­ряд­ка 1,5·10⁶ А/м она со­став­ля­ет со­тые до­ли нм.

З. э. обу­слов­лен на­ли­чи­ем у кван­то­вой сис­те­мы (напр., ато­ма) маг­нит­но­го мо­мен­та $μ$ , ко­то­рый свя­зан с её ме­ха­нич. мо­мен­том $\boldsymbol M$ и мо­жет ори­ен­ти­ро­вать­ся в про­стран­ст­ве лишь оп­ре­де­лён­ным об­ра­зом. Чис­ло воз­мож­ных ори­ен­та­ций $μ$ рав­но сте­пе­ни вы­ро­ж­де­ния уров­ня энер­гии. В маг­нит­ном по­ле атом с энер­ги­ей $ℰ$  и пол­ным маг­нит­ным мо­мен­том $μ$ при­об­ре­та­ет до­пол­нит. энер­гию $Δℰ = –μ_HH$, где $μ_H = gμ_БHm$ – про­ек­ция маг­нит­но­го мо­мен­та ато­ма на на­прав­ле­ние $\boldsymbol H$, ко­то­рая при­ни­ма­ет разл. зна­че­ния, $μ_Б$ – маг­не­тон Бо­ра, $m$ – маг­нит­ное кван­то­вое чис­ло, $g$ – мно­жи­тель Лан­де. Вы­ро­ж­де­ние уров­ня энер­гии сни­ма­ет­ся, и он рас­ще­п­ля­ет­ся на по­ду­ров­ни, чис­ло ко­то­рых рав­но сте­пе­ни вы­ро­ж­де­ния. Рас­ще­п­ле­ние спек­траль­ной ли­нии оп­ре­де­ля­ет­ся ха­рак­те­ром рас­ще­п­ле­ния уров­ней энер­гии, ме­ж­ду ко­то­ры­ми про­ис­хо­дит кван­то­вый пе­ре­ход, со­от­вет­ст­вую­щий ис­сле­дуе­мой ли­нии, а так­же от­бо­ра пра­ви­лам для маг­нит­но­го кван­то­во­го чис­ла $m$. Ес­ли рас­ще­п­ле­ние этих уров­ней энер­гии оди­на­ко­во, то на­блю­да­ет­ся зее­ма­нов­ский три­плет, в про­тив­ном слу­чае име­ет ме­сто слож­ная кар­ти­на рас­ще­п­ле­ния, при­чём для $Δm = 0$ по­лу­ча­ют­ся $π$-ком­по­нен­ты, для $Δm = ±1$ – $σ$-ком­по­нен­ты.

З. э. на­блю­да­ет­ся и в мо­ле­ку­ляр­ных спек­трах (обыч­но на вра­ща­тель­ных ли­ни­ях в ра­дио­диа­па­зо­не), од­на­ко его кар­ти­на слож­на и её рас­шиф­ров­ка пред­став­ля­ет боль­шие труд­но­сти. Для кри­стал­лов, имею­щих вы­ра­жен­ную дис­крет­ную струк­ту­ру спек­тров, обыч­но изу­ча­ют об­рат­ный эф­фект Зее­ма­на.

Изу­че­ние кар­ти­ны З. э. по­зво­ля­ет оп­ре­де­лять ха­рак­те­ри­сти­ки уров­ней энер­гии ато­мов и, сле­до­ва­тель­но, ин­тер­пре­ти­ро­вать атом­ные спек­тры. Кро­ме кван­то­вых пе­ре­хо­дов ме­ж­ду зее­ма­нов­ски­ми по­ду­ров­ня­ми, при­над­ле­жа­щи­ми раз­ным уров­ням энер­гии, про­ис­хо­дят пе­ре­хо­ды ме­ж­ду зее­ма­нов­ски­ми по­ду­ров­ня­ми од­но­го уров­ня. Час­то­ты та­ких пе­ре­хо­дов, как пра­ви­ло, ле­жат в СВЧ-диа­па­зо­не элек­тро­маг­нит­ных волн, они при­во­дят к из­би­ра­тель­но­му по­гло­ще­нию ра­дио­волн в па­ра­маг­нит­ных ве­ще­ст­вах, по­ме­щён­ных в маг­нит­ное по­ле, – элек­трон­но­му па­ра­маг­нит­но­му ре­зо­нан­су (ЭПР). На ос­но­ве ЭПР соз­да­ны при­бо­ры кван­то­вой элек­тро­ни­ки, в т. ч. кван­то­вые маг­ни­то­мет­ры для из­ме­ре­ния сла­бых маг­нит­ных по­лей в ла­бо­ра­тор­ных ус­ло­ви­ях и в кос­мо­се.