ВАВИ́ЛОВА – ЧЕРЕНКО́ВА ИЗЛУЧЕ́НИЕ

Рубрика: Физика
В книжной версии

Том 4. Москва, 2006, стр. 484-485
Скопировать библиографическую ссылку:

Книжная версия:

Электронная версия:

Авторы: И. М. Франк

ВАВИ́ЛОВА – ЧЕРЕНКО́ВА ИЗЛУЧЕ́НИЕ (Вавилова – Черенкова эффект, Черенкова – Вавилова излучение), излучение света электрически заряженной частицей при её движении в среде со скоростью, превышающей фазовую скорость света в этой среде. Обнаружено в 1934 П. А. Черенковым

при исследовании люминесценции растворов как слабое голубое свечение жидкостей под действием гамма-излучения. Эксперименты, осуществлённые Черенковым по инициативе и при участии С. И. Вавилова

, выявили характерные особенности обнаруженного явления: свечение наблюдается у всех чистых прозрачных жидкостей, причём яркость его слабо зависит от химич. состава жидкости, оно направлено под острым углом к первичному излучению и обладает характерной поляризацией, при этом не наблюдаются процессы тушения, присущие люминесценции. На основании результатов исследований Вавилов сделал основополагающее утверждение: обнаружен новый тип излучения, которое испускают движущиеся в жидкости быстрые электроны; такие электроны генерируются в веществе под действием гамма-излучения в результате Комптона эффекта

. (Свечение жидкостей под действием гамма-излучения наблюдалось ещё в 1920-х гг., однако не были установлены его особенности и не была доказана новизна явления.)

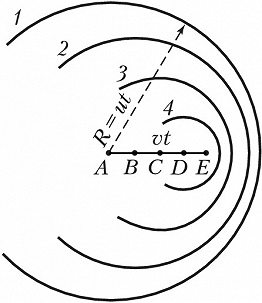
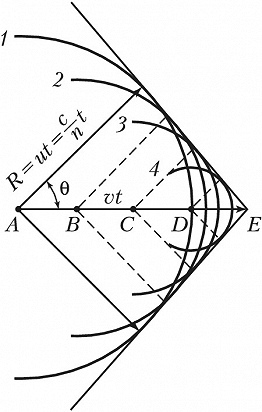
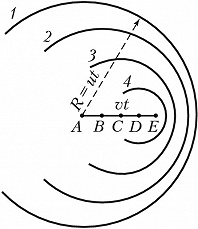
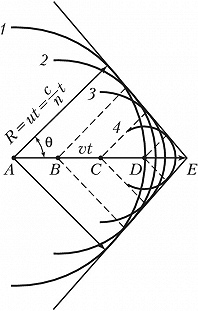
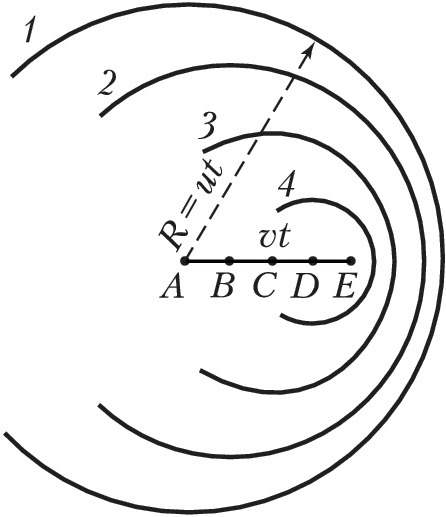
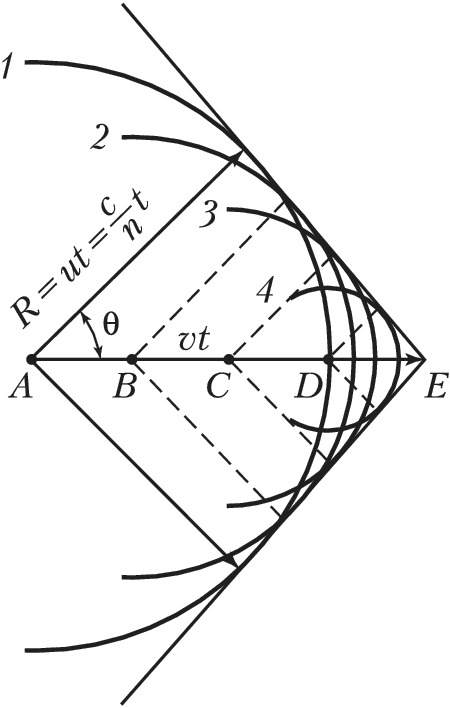
Количественная и качественная теория В.–Ч. и., основанная на уравнениях классич. электродинамики, предложена в 1937 И. Е. Таммом

и И. М. Франком

, квантовую теорию разработал в 1940 В. Л. Гинзбург

. Условия возникновения В.–Ч. и. и его направленность могут быть пояснены с помощью Гюйгенса – Френеля принципа

. Каждая точка траектории заряженной частицы (напр., точки

$A, B, C, D$ на рис. 1 и 2), согласно этому принципу, является источником волны, возникающей в момент прохождения через неё заряженной частицы. В оптически изотропной среде такие волны будут сферическими, т. к. они распространяются во все стороны с одинаковой скоростью

$u=c/n$ , где

$c$ - скорость света в вакууме,

$n$ - показатель преломления среды. Если частица, движущаяся со скоростью

$v$ , находится в момент наблюдения в точке

$E$ , то за

$t$ секунд до этого она находилась в точке

$A$ , т. е. на расстоянии от

$E$ , равном

$vt$ . Следовательно, волна, испущенная из точки

$A$ , к моменту наблюдения будет представлять собой сферу радиуса

$R=ut$ (окружность

$1$ на рис. 1). Волны, испущенные из точек

$B, C, D$ , в момент времени

$t$ будут представлены окружностями

$2, 3, 4$ . По принципу Гюйгенса такие парциальные волны в результате интерференции гасят друг друга всюду, за исключением их огибающей, которой соответствует волновая поверхность, распространяющаяся в среде.

Рис. 1. Движение заряженной частицы в среде со скоростью

${v \lt u}$ . Окружности

${1, 2, 3, 4}$ - положения парциальных волн, испущенных частицей из точек

${A, B, C, D}$ соответственно.

Если скорость частицы $v$ меньше скорости света $u$ в данной среде, то парциальные волны общей огибающей не имеют (рис. 1), т. к. они с течением времени всё больше обгоняют частицу. В этом случае электрич. заряд, двигаясь равномерно и прямолинейно, электромагнитное излучение не испускает.

В случае когда

$v\gt u=c/n, или\;\beta n\gt1\qquad(1)$

Рис. 2. Движение заряженной частицы в среде со скоростью

$v \gt u$ ;

$\theta$ – угол между направлением волнового вектора возникающего излучения и скоростью частицы.

(где $\beta = v/c$ ), т. е. когда частица движется быстрее, чем распространяются световые волны в среде, соответствующие им сферы пересекаются (рис. 2) и их общая огибающая (волновая поверхность) образует конус с вершиной в точке $E$ , где в данный момент находится частица. Нормаль к образующим конуса определяет волновые векторы, т. е. направление распространения испускаемого частицей излучения. Угол между волновым вектором и направлением движения частицы удовлетворяет соотношению:

$\cos \theta = u/v=c/(nv)=1/(\beta n).\qquad(2)$

(Для оптически анизотропных сред излучение возникает под двумя разл. углами к направлению движения частицы, соответствующими обыкновенному и необыкновенному лучам.) В оптически изотропной среде частица с зарядом $e$ , прошедшая расстояние в 1 см со скоростью $v \gt u$ , излучает энергию

$E=(e/c)^2 \int\limits_{\beta n(\omega) \gt 1} \, \omega[1-1/{\{ \beta n(\omega)\}}^2] d\omega \qquad(3)$

(где $\omega = 2nc/\lambda$ – циклическая частота излучения, $\lambda$ – его длина волны в вакууме). Подынтегральное выражение описывает распределение энергии в спектре В.–Ч. и., а область интегрирования ограничена условием $(1)$ .

В.–Ч. и. возникает при движении любой заряженной частицы в среде, если для неё выполняется условие $(1)$ . Для электронов это условие выполняется уже при энергиях порядка 10⁵ эВ (такими энергиями обладают мн. электроны радиоактивных процессов). Более тяжёлые частицы должны иметь более высокую энергию, напр. протон – энергию порядка 10⁸ эВ.

На основе В.–Ч. и. разработаны эксперим. методы для регистрации частиц и изучения их природы (см. Черенковский счётчик

). Измерение угла

$\theta$ в среде с известным

$n$ позволяет установить по формуле

$(1)$ или

$(2)$ скорость частицы. Определив скорость и энергию частицы, можно по отклонению её траектории в магнитном поле рассчитать массу частицы (так была установлена масса антипротона при его открытии). Для очень быстрых частиц условие

$(1)$ начинает выполняться уже в сжатых газах (газовые черенковские счётчики). В.–Ч. и., возникающее при движении частиц космич. лучей в атмосфере, используется для их изучения.

В.–Ч. и. в чистом виде может наблюдаться только в том случае, когда частица движется с постоянной скоростью в неограниченной однородной среде. При пересечении границ сред возникает переходное излучение

. При изменении скорости частицы возникает тормозное излучение

. В 1940 Э. Ферми

внёс в теорию В.–Ч. и. существенные уточнения, приняв во внимание способность реальной среды поглощать свет, по крайней мере, в некоторых областях спектра.

В.–Ч. и. – пример оптики «сверхсветовых» скоростей. Оно экспериментально изучено в разл. средах, теоретически рассмотрено излучение электрич. и магнитных диполей и мультиполей. Ожидаемые свойства излучения движущегося магнитного заряда использовались для поисков магнитного монополя. Рассмотрено излучение частицы в канале среды (напр., в волноводе). При В.–Ч. и. новые особенности приобретает Доплера эффект

в среде: появляются т. н. аномальный и сложный эффекты Доплера. Можно полагать, что всякая система частиц, способная взаимодействовать с электромагнитным полем, будет излучать свет за счёт своей кинетич. энергии, если её скорость превышает фазовую скорость света. Теоретич. представления, лежащие в основе В.–Ч. и., тесно связаны с др. проблемами совр. физики – волнами Маха в акустике, вопросами устойчивости движения частиц в плазме и генерации в ней волн, генерацией и усилением электромагнитных волн и т. д.

За открытие и создание теории В.– Ч. и. в 1958 И. Е. Тамм, И. М. Франк и П. А. Черенков удостоены Нобелевской пр. В.–Ч. и. в зарубежной лит-ре называют черенковским излучением.

Библиография

Лит.: Черенков П. А. Видимое свечение чистых жидкостей под действием γ-радиации // Доклады АН СССР. 1934. Т. 2. № 8; Вавилов С. И. О возможных причинах синего γ-свечения жидкостей // Там же; Тамм И. Е., Франк И. М. Когерентное излучение быстрого электрона в среде // Там же. 1937. Т. 14. № 3; Черенков П. А., Тамм И. Е., Франк И. М. Нобелевские лекции. М., 1960.

Иллюстрации

Рис. 1. Движение заряженной частицы в среде со скоростью ${v \lt u}$ . Окружности ${1, 2, 3, 4}$ - положения парциальных волн, испущенных частицей из точек ${A, B, C, D}$ соответственно.
Рис. 2. Движение заряженной частицы в среде со скоростью $v \gt u$ ; $\theta$ – угол между направлением волнового вектора возникающего излучения и скоростью частицы.

prev next

Вернуться к началу

ВАВИ́ЛОВА – ЧЕРЕНКО́ВА ИЗЛУЧЕ́НИЕ

Ссылка на статью на E-mail

Спасибо!

Подписка на рассылку новостей