КО́МПТОНА ЭФФЕ́КТ

КО́МПТОНА ЭФФЕ́КТ (ком­пто­нов­ское рас­сея­ние), рас­сея­ние жё­ст­ко­го (ко­рот­ко­вол­но­во­го) элек­тро­маг­нит­но­го из­лу­че­ния на сво­бод­ных за­ря­жен­ных час­ти­цах, со­про­во­ж­даю­щее­ся из­ме­не­ни­ем дли­ны вол­ны рас­се­ян­но­го из­лу­че­ния. От­крыт А. Комп­то­ном в 1922 при рас­сея­нии жё­ст­ких рент­ге­нов­ских лу­чей в гра­фи­те, атом­ные элек­тро­ны ко­то­ро­го, рас­сеи­ваю­щие из­лу­че­ние, мо­гут с хо­ро­шей точ­но­стью рас­смат­ри­вать­ся как сво­бод­ные (по­сколь­ку час­то­та рент­ге­нов­ских лу­чей на­мно­го пре­вос­хо­дит ха­рак­тер­ные час­то­ты дви­же­ния элек­тро­нов в лёг­ких ато­мах). Со­глас­но из­ме­ре­ни­ям Ком­пто­на, пер­во­на­чаль­ная дли­на вол­ны рент­ге­нов­ско­го из­лу­че­ния $λ_0 $ при рас­сея­нии его на угол $\theta$ уве­ли­чи­ва­лась и ока­зы­ва­лась рав­ной$λ′=λ_0+λ_C (1-\cos \theta) \tag 1, $ где $λ_C$ – по­сто­ян­ная для всех ве­ществ ве­ли­чи­на, на­зван­ная ком­пто­нов­ской дли­ной вол­ны элек­тро­на. (Бо­лее час­то упот­реб­ля­ет­ся ве­ли­чи­на $\bar\lambda_C$=$λ/2π=3,86159268·10^{–11} $см.) К. э. рез­ко про­ти­во­ре­чит клас­сич. вол­но­вой тео­рии све­та, со­глас­но ко­то­рой дли­на вол­ны элек­тро­маг­нит­но­го из­лу­че­ния не долж­на ме­нять­ся при его рас­сея­нии на сво­бод­ных элек­тро­нах. По­это­му от­кры­тие К. э. яви­лось од­ним из важ­ней­ших фак­тов, ука­зав­ших на двой­ст­вен­ную при­ро­ду све­та (см. Кор­пус­ку­ляр­но-вол­но­вой дуа­лизм). Объ­яс­не­ние эф­фек­та, дан­ное Ком­пто­ном и, не­за­ви­си­мо от него, П. Де­ба­ем, за­клю­ча­ет­ся в том, что $\gamma$-квант с энер­ги­ей $ℰ=ℏω$ и им­пуль­сом $\boldsymbol p=ℏ \boldsymbol k$, стал­ки­ва­ясь с элек­тро­ном, пе­ре­да­ёт ему в за­ви­си­мо­сти от уг­ла рас­сея­ния часть сво­ей энер­гии. (Здесь $\hbar$ – по­сто­ян­ная План­ка, $\omega$ – цик­ли­че­ская час­то­та элек­тро­маг­нит­ной вол­ны, $\boldsymbol k$  – её вол­но­вой век­тор $\boldsymbol{|k|}=\omega/c$, свя­зан­ный с дли­ной вол­ны со­от­но­ше­ни­ем $\lambda= 2\pi / \boldsymbol {|k|}$.) Со­глас­но за­ко­нам со­хра­не­ния энер­гии и им­пуль­са, энер­гия $γ$-кван­та, рас­се­ян­но­го на по­коя­щем­ся элек­тро­не, рав­на$$ℰ'=\frac{ℰ}{1+ℰ/mc^2(1-\cos \theta)}, \tag 2 $$что пол­но­стью со­от­вет­ст­ву­ет дли­не вол­ны рас­се­ян­но­го из­лу­че­ния $λ′$. При этом ком­пто­нов­ская дли­на вол­ны элек­тро­на вы­ра­жа­ет­ся че­рез фун­дам. по­сто­ян­ные: мас­су элек­тро­на $m_e$, ско­рость све­та с и по­сто­ян­ную План­ка $\hbar:\bar\lambda_C=\hbar/m_ec$. Пер­вым ка­че­ст­вен­ным под­твер­жде­ни­ем та­кой ин­тер­пре­та­ции К. э. бы­ло на­блю­де­ние в 1923 Ч. Т. Р. Виль­со­ном элек­тро­нов от­да­чи при об­лу­че­нии воз­ду­ха рент­ге­нов­ски­ми лу­ча­ми в изо­бре­тён­ной им ка­ме­ре (ка­ме­ре Виль­со­на). Под­роб­ные ко­ли­че­ст­вен­ные ис­сле­до­ва­ния К. э. бы­ли про­ве­де­ны Д. В. Ско­бель­цы­ным, ис­поль­зо­вав­шим в ка­че­ст­ве ис­точ­ни­ка γ-кван­тов вы­со­ких энер­гий ра­дио­ак­тив­ный пре­па­рат RaC (²¹⁴Bi), а в ка­че­ст­ве де­тек­то­ра – ка­ме­ру Виль­со­на, по­ме­щён­ную в маг­нит­ное по­ле. Дан­ные Ско­бель­цы­на бы­ли в даль­ней­шем ис­поль­зо­ва­ны для про­вер­ки кван­то­вой элек­тро­ди­на­ми­ки. В ре­зуль­та­те этой про­вер­ки швед. фи­зик О. Клейн, япон. фи­зик Й. Ни­ши­на и И. Е. Тамм уста­но­ви­ли, что эф­фек­тив­ное се­че­ние К. э. убы­ва­ет с рос­том энер­гии γ-кван­тов (т. е. с умень­ше­ни­ем дли­ны вол­ны элек­тро­маг­нит­но­го из­лу­че­ния), а при дли­нах волн, зна­чи­тель­но пре­вы­шаю­щих ком­пто­нов­скую, стре­мит­ся к пре­де­лу $\sigma_T=(8\pi/3)r_e^2=0, 6652459\cdot 10^{24}$ см², ука­зан­но­му Дж. Дж. Том­со­ном на ос­но­ве вол­но­вой тео­рии ($r_e=e^2/m_ec^2 $— клас­сич. ра­ди­ус элек­тро­на).

К. э. на­блю­да­ет­ся при рас­сея­нии $γ$ -кван­тов не толь­ко на элек­тро­нах, но и на др. час­ти­цах с боль­шей мас­сой, од­на­ко эф­фек­тив­ное се­че­ние при этом на неск. по­ряд­ков мень­ше.

В слу­чае ко­гда $γ$-квант рас­сеи­ва­ет­ся не на по­коя­щем­ся, а на дви­жу­щем­ся (в осо­бен­но­сти на ре­ля­ти­ви­ст­ском) элек­тро­не, воз­мож­на пе­ре­да­ча энер­гии от элек­тро­на $γ$-кван­ту. Это яв­ле­ние на­зы­ва­ют об­рат­ным эф­фек­том Комп­то­на.

Зависимость коэффициента полного поглощения (μ) γ-излучения в свинце (Pb) и алюминии (Al) от энергии γ-квантов (сплошные кривые). Штриховые линии – отдельные вклады, вносимые фото...

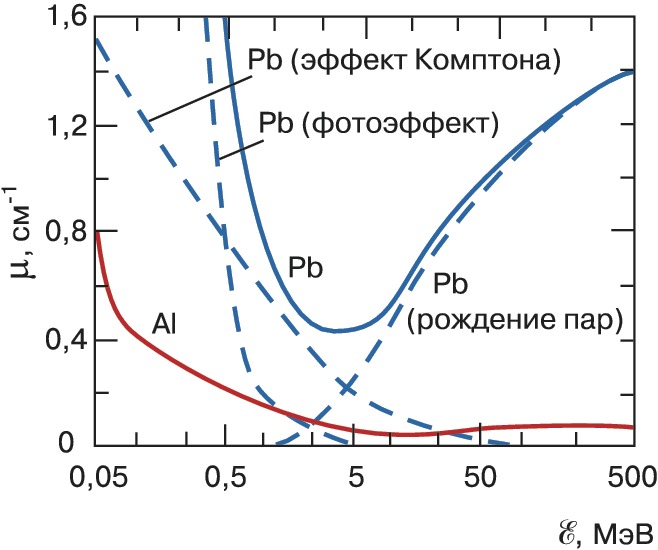
К. э., на­ря­ду с фо­то­эф­фек­том и ро­ж­де­ни­ем элек­трон-по­зи­трон­ных пар, яв­ля­ет­ся осн. ме­ха­низ­мом по­гло­ще­ния жё­ст­ко­го элек­тро­маг­нит­но­го из­лу­че­ния в ве­ще­ст­ве. От­но­сит. роль К. э. за­ви­сит от атом­но­го но­ме­ра эле­мен­та и энер­гии $γ$-кван­тов. В свин­це, напр., К. э. да­ёт осн. вклад в по­те­рю фо­то­нов в об­лас­ти энер­гий 0,5–5 МэВ, в алю­ми­нии – в диа­пазо­не 0,05–15 МэВ (рис.). В этой об­лас­ти энер­гий ком­пто­нов­ское рас­сея­ние ис­поль­зу­ет­ся для де­тек­ти­ро­ва­ния $γ$-кван­тов и из­ме­ре­ния их энер­гии.

Важ­ную роль К. э. иг­ра­ет в ас­т­ро­фи­зи­ке и кос­мо­ло­гии. Напр., он оп­ре­де­ля­ет про­цесс пе­ре­но­са энер­гии фо­то­на­ми из центр. об­лас­тей звёзд (где про­ис­хо­дят тер­мо­ядер­ные ре­ак­ции) к их по­верх­но­сти, т. е. в ко­неч­ном счё­те све­ти­мость звёзд и темп их эво­лю­ции. Све­то­вое дав­ле­ние, вы­зы­вае­мое рас­сея­ни­ем, оп­ре­де­ля­ет кри­ти­че­скую све­ти­мость звёзд, на­чи­ная с ко­то­рой обо­лоч­ка звез­ды на­чи­на­ет рас­ши­рять­ся.

В ран­ней рас­ши­ряю­щей­ся Все­лен­ной ком­пто­нов­ское рас­сея­ние под­дер­жи­ва­ло рав­но­вес­ную темп-ру ме­ж­ду ве­ще­ст­вом и из­лу­че­ни­ем в го­ря­чей плаз­ме из про­то­нов и элек­тро­нов вплоть до об­ра­зо­ва­ния из этих ча­стиц ато­мов во­до­ро­да. Бла­го­да­ря это­му уг­ло­вая ани­зо­тро­пия ре­лик­то­во­го из­лу­че­ния да­ёт ин­фор­ма­цию о пер­вич­ных флук­туа­ци­ях ве­ще­ст­ва, при­во­дя­щих к об­ра­зо­ва­нию круп­но­мас­штаб­ной струк­ту­ры Все­лен­ной. Об­рат­ным К. э. объ­яс­ня­ют су­ще­ст­во­ва­ние рент­ге­нов­ской ком­по­нен­ты фо­но­во­го га­лак­тич. из­лу­че­ния и $γ$-из­лу­че­ния не­ко­то­рых кос­мич. ис­точ­ни­ков. При про­хо­ж­де­нии ре­лик­то­во­го из­лу­че­ния че­рез об­ла­ка го­ря­че­го га­за в да­лё­ких га­лак­ти­ках бла­го­да­ря об­рат­но­му К. э. воз­ни­ка­ют ис­ка­же­ния в спек­тре ре­лик­то­во­го из­лу­че­ния, даю­щие важ­ную ин­фор­ма­цию о Все­лен­ной (см. Сю­няе­ва – Зель­до­ви­ча эф­фект).

Об­рат­ный К. э. по­зво­ля­ет по­лу­чать ква­зи­мо­но­хро­ма­тич. пуч­ки $γ$-кван­тов вы­со­кой энер­гии пу­тём рас­сея­ния ла­зер­но­го из­лу­че­ния на встреч­ном пуч­ке ус­ко­рен­ных ульт­ра­ре­ля­ти­ви­ст­ских элек­тро­нов. В не­ко­то­рых слу­ча­ях об­рат­ный К. э. пре­пят­ст­ву­ет осу­ще­ст­в­ле­нию тер­мо­ядер­ных ре­ак­ций син­те­за в зем­ных ус­ло­ви­ях.