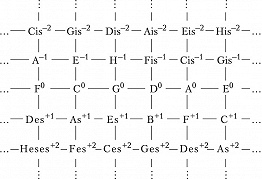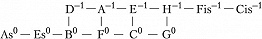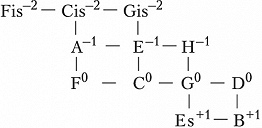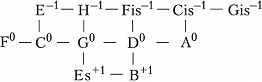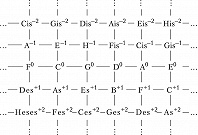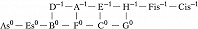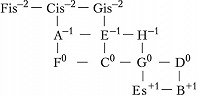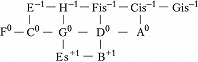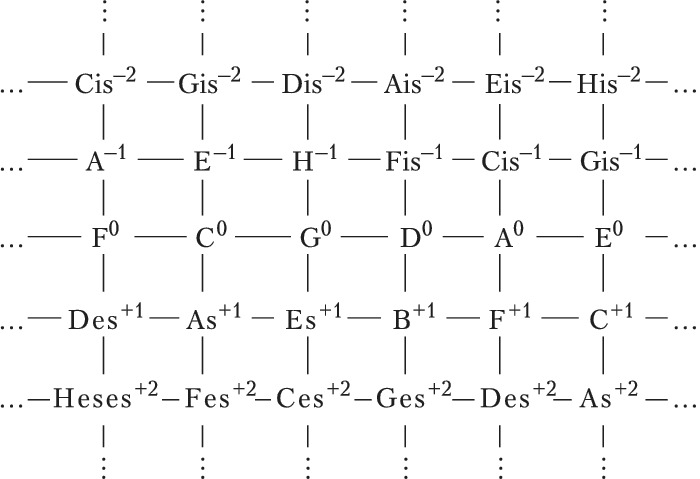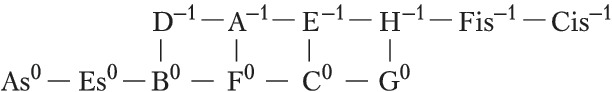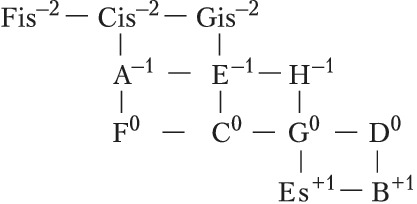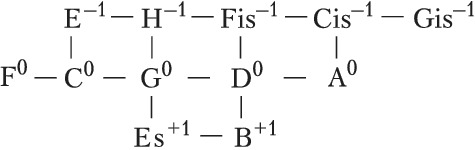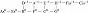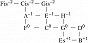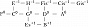ЧИСТЫЙ СТРОЙ

Рис. 1.

ЧИ́СТЫЙ СТРОЙ (нем. reine Stimmung, англ. just intonation, pure intonation), строй му­зы­каль­ный, по­ро­ж­дае­мый ин­тер­ва­ла­ми, от­но­ше­ния час­тот зву­ков ко­то­рых вы­ра­жа­ют­ся от­но­ше­ния­ми не­боль­ших на­ту­раль­ных чи­сел. Та­кие по­ро­ж­даю­щие строй ин­тер­ва­лы не да­ют бие­ний, т. е. яв­ля­ют­ся аку­сти­че­ски чис­ты­ми. Обыч­но чис­тым на­зы­ва­ют квин­то-тер­цо­вый строй, по­ро­ж­дён­ный ок­та­вой (2:1), чис­той квин­той (3:2) и чис­той боль­шой тер­ци­ей (5:4). Его схе­ма в ви­де квад­ратной ре­шёт­ки, вос­хо­дя­щая к Л. Эй­ле­ру (1773), при­ве­де­на на рис. 1.

Б. Рамос де Пареха (1482)

Л. Фольяно (1529, 2-й вариант)

И. Кеплер (1619, 1-й вариант)   Рис. 2.

Здесь изо­бра­же­ны сту­пе­ни с точ­но­стью до ок­та­вы; го­ри­зон­таль­ные рёб­ра со­от­вет­ст­ву­ют чис­тым квин­там, вер­ти­каль­ные – чис­тым боль­шим тер­ци­ям; це­лое чис­ло в над­строч­ном ин­дек­се обо­зна­ча­ет ко­ли­че­ст­во син­то­ни­че­ских комм, на ко­то­рое по­вы­ша­ет­ся или по­ни­жа­ет­ся сту­пень от­но­си­тель­но сво­его по­ло­же­ния в не­ко­то­рой фик­си­ро­ван­ной це­пи чис­тых квинт, при­ни­мае­мой за «ну­ле­вой» уро­вень от­счё­та (т. н. но­та­ция К. Ай­ца, англ. С. Eitz’s notation). Схе­ма от­ра­жа­ет аб­ст­ракт­но-ма­те­ма­тич. струк­ту­ру Ч. с., в ко­то­рой ко­ли­че­ст­во сту­пе­ней в ок­та­ве мыс­лит­ся бес­ко­неч­ным; на прак­ти­ке рас­смат­ри­ва­ют­ся ко­неч­ные об­лас­ти ука­зан­ной ре­шёт­ки. Так, ис­то­ри­че­ские 12-сту­пен­ные строи (ка­ж­дый из ко­то­рых пред­став­ля­ет со­бой ва­ри­ант ко­неч­но­го Ч. с.) со­от­вет­ст­ву­ют разл. ко­неч­ным связ­ным её об­лас­тям (рис. 2).

Та­кие об­лас­ти, ох­ва­ты­ваю­щие ма­лое чис­ло сту­пе­ней, от­ли­ча­ют­ся не­од­но­род­но­стью сво­ей струк­ту­ры (в ча­ст­но­сти, квин­ты ти­па G⁰–D^–1, B⁺¹–F⁰ от­ли­ча­ют­ся от чис­тых на ком­му и зву­чат чрез­вы­чай­но рез­ко) и по­это­му тре­бу­ют тем­пе­ра­ции. Вме­сте с тем бо́льшие об­лас­ти мо­гут быть су­ще­ст­вен­но од­но­род­нее: та­ко­ва, напр., 53-сту­пен­ная об­ласть спец. ви­да, впер­вые де­таль­но рас­смот­рен­ная С. Та­на­кой (1890). В ней, в ча­ст­но­сти, при­сут­ст­ву­ют ин­тер­ва­лы ти­па Cis^–1–As⁰ (на­зы­вае­мые схиз­ма­ти­че­ски­ми квин­та­ми, см. в ст. Схиз­ма и ди­ас­хиз­ма), аку­сти­че­ски не­от­ли­чи­мые от квинт рав­но­мер­но-тем­пе­ри­ро­ван­но­го строя. Cтрой, опи­сан­ный Та­на­кой, чрез­вы­чай­но бли­зок к 53-сту­пен­но­му рав­но­мер­но­му строю. 53-сту­пен­ные строи бы­ли реа­ли­зо­ва­ны в не­ко­то­рых экс­пе­рим. муз. ин­ст­ру­ментах с не­стан­дарт­ны­ми кла­виа­ту­ра­ми разл. ди­зай­на (напр., кла­виа­ту­ра Л. Хэн­со­на, 1942). В совр. аку­сти­ке по­ня­тие Ч. с. обоб­ща­ет­ся до по­ня­тия «чис­то­го строя пре­де­ла p» (англ. p-limit just intonation), где p – про­стое чис­ло. От­но­ше­ния час­тот зву­ков всех ин­тер­ва­лов та­ко­го строя вы­ра­жа­ют­ся чис­ла­ми, про­стые де­ли­те­ли ко­то­рых не пре­вос­хо­дят p. В этой тер­ми­но­ло­гии пи­фа­го­ров строй – это Ч. с. пре­де­ла 3, квин­то-тер­цо­вый строй – Ч. с. пре­де­ла 5. Су­ще­ст­ву­ют экс­пе­рим. муз. ин­ст­ру­мен­ты (в т. ч. элек­трон­ные) для иг­ры в чис­тых стро­ях бо­лее вы­со­ких пре­де­лов.