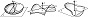ПОВЕ́РХНОСТЕЙ ТЕО́РИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ПОВЕ́РХНОСТЕЙ ТЕО́РИЯ, раздел дифференциальной геометрии, в котором изучаются свойства поверхностей. В классич. П. т. рассматриваются свойства поверхностей, не меняющиеся при их движении. Одна из осн. задач классич. П. т. – задача измерений на поверхности – возникла в геодезии, т. е. связана с измерениями на поверхности Земли. Совокупность фактов, связанных с измерениями на поверхности, составляет внутреннюю геометрию поверхности. К внутренней геометрии поверхностей относятся такие понятия, как длина линии, угол между двумя направлениями, площадь области, а также геодезич. линии, геодезич. кривизна линии и мн. др.
Внутреннюю геометрию определяет первая квадратичная форма поверхности $$ds^2=Edu^2+2Fdudv+Gdv^2\tag1$$ (здесь $E= (r_u,r_u), F= (r_u,r_v), G=(r_v,r_v), r_u=∂r/∂u, r_v=∂r/∂v, r=r(u,v)$ – радиус-вектор точки поверхности, $u,v$ – её криволинейные координаты, $(·,·)$ означает скалярное произведение), выражающая квадрат дифференциала дуги линии на поверхности. Если известны функции $E=E(u,v), F=F(u,v), G=G(u,v)$, то, зная внутренние уравнения линии $u=u(t), v=v(t)$ и интегрируя $ds$, можно определить длину этой линии; кроме того, существуют формулы, которые при данных $E, F, G$ выражают угол между двумя линиями и площадь области по внутренним уравнениям этих линий и по внутреннему уравнению контура области.
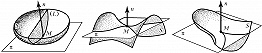
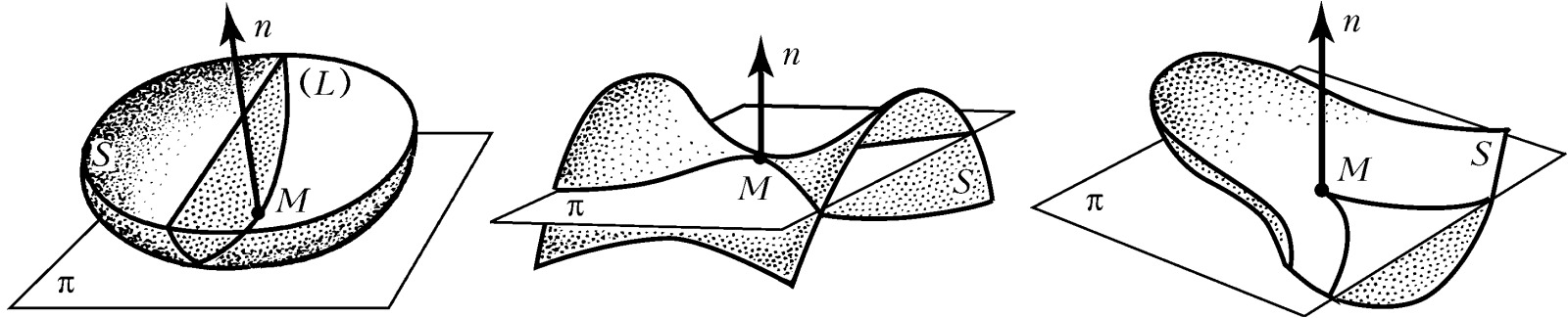
Изучение пространственного строения окрестности точки на поверхности производится при помощи второй квадратичной формы поверхности $$2h=Ldu^2+2Mdudv+Ndv^2\tag2$$ (здесь $L=(r_{uu},n), M=(r_{uv},n), N =(r_{vv},n), n=[r_u,r_v]/ ∣ [r_u,r_v] ∣$ – единичный вектор нормали к поверхности, $[·,·]$ означает векторное произведение). Величина $h$ с точностью до малых более высокого порядка относительно $du$, $dv$ равна расстоянию от точки $M′$ поверхности с координатами $u+du, v+dv$ до касательной плоскости $π$ в точке $M$ с координатами $u, v$, причём расстояние берётся со знаком, зависящим от того, с какой стороны от $π$ расположена точка $M$. Если форма (2) знакоопределённая, то поверхность в достаточно малой окрестности точки $M$ располагается по одну сторону от касательной плоскости $π$, и в этом случае точка $M$ поверхности называется эллиптической (рис. 1). Если форма (2) знакопеременная, то поверхность в окрестности точки $M$ располагается по разные стороны от плоскости $π$, и точка $M$ тогда называется гиперболической (рис. 2). Если форма (2) – знакоопределённая, но принимает нулевые значения (при не равных одновременно нулю $du$ и $dv$), то точка $M$ называется параболической (на рис. 3 показан один из примеров строения поверхности в окрестности параболич. точки).
Более точная характеристика пространственной формы поверхности может быть получена с помощью исследования геометрич. свойств линий на поверхности. Пусть $M$ – некоторая точка на поверхности $S$ и $n$ – единичный вектор нормали к поверхности в $M$. Линия $L$ пересечения $S$ с плоскостью, проходящей через $n$ в направлении $dr=r_udu+r_vdv$, называется нормальным сечением в этом направлении, а её кривизна – нормальной кривизной. Нормальная кривизна $1/R$ вычисляется по формуле $$\frac{1}{R}=\frac{Ldu^2+2Mdudv+Ndv^2}{Edu^2+2Fdudv+Gdv^2}.$$
Экстремальные значения нормальной кривизны в данной точке называются главными кривизнами, а соответствующие направления на поверхности – главными направлениями. Если главные кривизны в точке $M$ различны, то в этой точке существуют два главных направления. Линии, направления которых в каждой точке являются главными, называются линиями кривизны. Направления, в которых нормальная кривизна равна нулю, называются асимптотическими, а линии, имеющие в каждой точке асимптотич. направление, – асимптотич. линиями. Поверхность, состоящая из эллиптич. точек (напр., сфера), не имеет асимптотич. линий. Поверхность, состоящая из гиперболич. точек, имеет два семейства асимптотич. линий (напр., две системы прямолинейных образующих однополостного гиперболоида). Поверхность, состоящая из параболич. точек, имеет одну систему асимптотич. линий – систему прямолинейных образующих.
Дальнейшее изучение свойств произвольных линий на поверхности (в первую очередь кривизн линий) тесно связано с кривизнами нормальных сечений. Кривизна в данной точке произвольной линии на поверхности может быть вычислена через кривизну нормального сечения с помощью формулы Мёнье (см. Мёнье теорема), а кривизна произвольного нормального сечения в данной точке связана простым соотношением (Эйлера формулой) с главными кривизнами.
Поверхности, между точками которых можно установить такое взаимно однозначное соответствие, что длины соответствующих линий равны, называются изометричными. Изометричные поверхности имеют одинаковую геометрию, но их пространственное строение может быть различным, и главные кривизны в соответствующих точках у них могут быть также различными (напр., окрестность точки на плоскости изометрична некоторой окрестности точки на цилиндре, но имеет иную пространственную структуру). Однако произведение $K$ главных кривизн $1/R_1$ и $1/R_2$ не меняется при изометричных преобразованиях поверхности (теорема Гаусса, 1827) и поэтому может служить внутр. мерой искривлённости поверхности в данной точке. Величина $K$ называется полной или гауссовой кривизной поверхности в точке $M$ и выражается формулой $$K=\frac{LN-M^2}{EG-F^2};\tag3$$ полная кривизна в соответствии с теоремой Гаусса может быть выражена только через коэффициенты первой квадратичной формы и их производные. Приведённая выше классификация точек регулярной поверхности может быть сопоставлена со значениями полной кривизны: в эллиптич. точках она положительна, в гиперболических – отрицательна, в параболических – равна нулю.
Важное значение в П. т. имеет вопрос о возможности изгибания поверхности, который можно сформулировать следующим образом: можно ли включить данную регулярную поверхность в однопараметрич. семейство изометричных неконгруэнтных регулярных поверхностей (конгруэнтные поверхности – поверхности, совмещаемые движением)? При этом рассматриваются как сама возможность изгибания, так и изгибания спец. вида.
Задача изгибания поверхностей тесно связана с задачей определения поверхности по заданным основным квадратичным формам. Поскольку значение полной кривизны $K$ поверхности может быть выражено через коэффициенты первой квадратичной формы, то уравнение (3) является одним из соотношений, связывающих коэффициенты первой (1) и второй (2) форм. Другие два соотношения $$\frac{\partial\Delta}{\partial v}-\frac{\partial\Delta'}{\partial u}+Γ^{2}_{22}\Delta-2Γ^2_{12}\Delta'+Γ^2_{11}\Delta''=0, \\ \frac{\partial\Delta''}{\partial u}-\frac{\partial\Delta'}{\partial v}+Γ^{1}_{22}\Delta-2Γ^1_{12}\Delta'+Γ^1_{11}\Delta''=0,\tag4$$
где $\Delta=\frac{L}{\sqrt{EG-F^2}}, \Delta'=\frac{M}{\sqrt{EG-F^2}}, \Delta''=\frac{N}{\sqrt{EG-F^2}}, Γ^i_{jk}$ – т. н. символы Кристоффеля второго рода, были установлены К. М. Петерсоном (1853). Справедливо и обратное утверждение: если коэффициенты двух форм, одна из которых положительно определённая, удовлетворяют уравнениям (3) и (4), то существует определённая с точностью до движения и зеркального отражения поверхность, для которой указанные формы будут первой и второй квадратичными формами (теорема Боннэ).
С нач. 20 в. в классич. П. т. появляется новое направление, в котором исследуется поверхность «в целом» по данным свойствам окрестностей её точек. Важные результаты в этой области получены Л. А. Люстерником и Л. Г. Шнирельманом, которыми утвердительно была решена проблема существования трёх замкнутых геодезических линий на регулярных замкнутых поверхностях, гомеоморфных сфере. Принципиально новые результаты были получены А. Д. Александровым и А. В. Погореловым в теории выпуклых поверхностей. Александров предложил новый метод исследования выпуклых поверхностей, основанный на приближении выпуклых поверхностей многогранниками. Н. В. Ефимов получил фундам. результаты по теории поверхностей отрицательной кривизны.
Рассмотренные свойства поверхностей не меняются при любых изометрич. преобразованиях всего пространства, т. е. они относятся к т. н. метрической П. т. Изучаются также свойства поверхностей, инвариантные по отношению к др. группам преобразований пространства, напр. к группе аффинных или проективных преобразований. Аффинная П. т. рассматривает свойства поверхностей, неизменные при эквиаффинных преобразованиях (аффинные преобразования, сохраняющие объём). Проективная П. т. рассматривает проективно инвариантные свойства поверхностей.