МЁНЬЕ́ ТЕОРЕ́МА

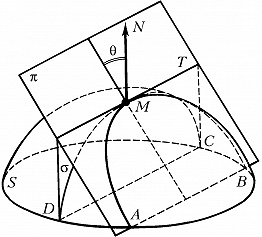
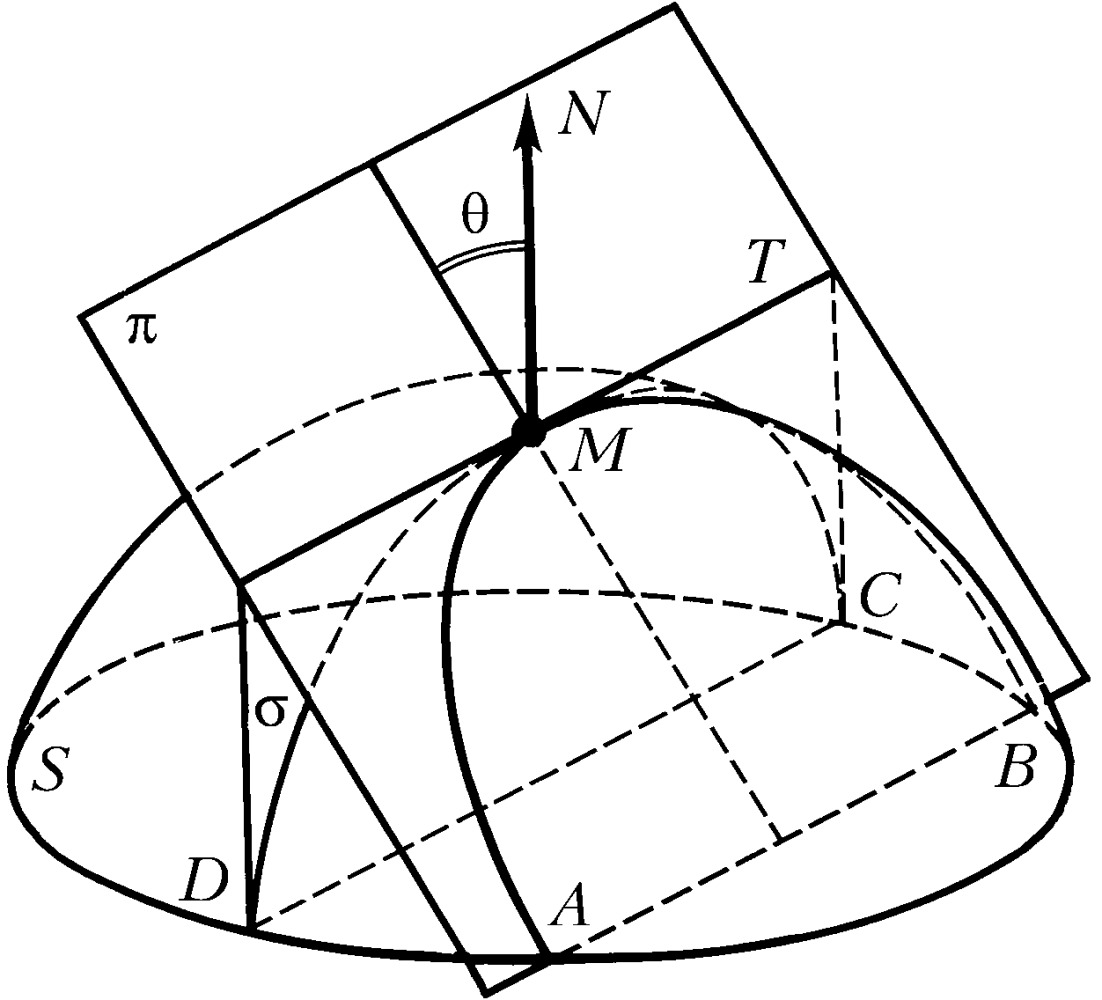
МЁНЬЕ́ ТЕОРЕ́МА, тео­ре­ма диф­фе­рен­ци­аль­ной гео­мет­рии, свя­зы­ваю­щая кри­виз­ны пло­ских се­че­ний по­верх­но­сти (см. Кри­виз­на). Пусть $π$ – про­из­воль­ная плос­кость, про­ве­дён­ная че­рез ка­са­тель­ную $MT$ к по­верх­но­сти $S$ в точ­ке $M$ (рис.), $θ$ – её угол с нор­ма­лью $MN$ к по­верх­но­сти, $^1/_R$ – кри­виз­на в точ­ке $M$ кри­вой $DMC$, по ко­то­рой по­верх­ность $S$ пе­ре­се­ка­ет­ся плос­ко­стью $σ$, про­хо­дя­щей че­рез нор­маль $MN$ и пря­мую $MT$ ($DMC$ – т. н. нор­маль­ное се­че­ние по­верх­но­сти). То­гда кри­виз­на $^1/_ρ$ в точ­ке $M$ кри­вой $AMB$, по ко­то­рой по­верх­ность $S$ пе­ре­се­ка­ет­ся плос­ко­стью $σ$ , свя­за­на с кри­виз­ной $^1/_R$ нор­маль­но­го се­че­ния со­от­но­ше­ни­ем

$\frac{1}{\rho }cos\:\Theta =\frac{1}{R},$

на­зы­вае­мым фор­му­лой Мё­нье. Эта тео­ре­ма ус­та­нов­ле­на Ж. Мё­нье в 1776 (опубл. в 1785).