ФРЕНЕ́ЛЯ ФО́РМУЛЫ

ФРЕНЕ́ЛЯ ФО́РМУЛЫ, оп­ре­де­ля­ют от­но­ше­ния ам­пли­ту­ды, фа­зы и со­стоя­ния по­ля­ри­за­ции пре­лом­лён­ной и от­ра­жён­ной пло­ских элек­тро­маг­нит­ных волн при про­хо­ж­де­нии их че­рез пло­скую гра­ни­цу раз­де­ла двух про­зрач­ных сред. Ус­та­нов­ле­ны О. Фре­не­лем

в 1823. Ф. ф. сле­ду­ют так­же из Мак­свел­ла урав­не­ний

 >>

с учё­том ус­ло­вий не­раз­рыв­но­сти не­ко­то­рых со­став­ляю­щих элек­тро­маг­нит­но­го по­ля.

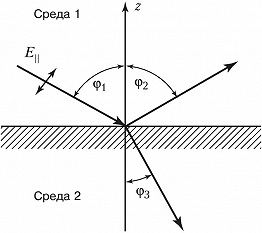
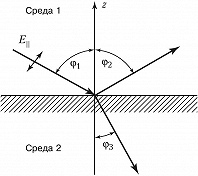
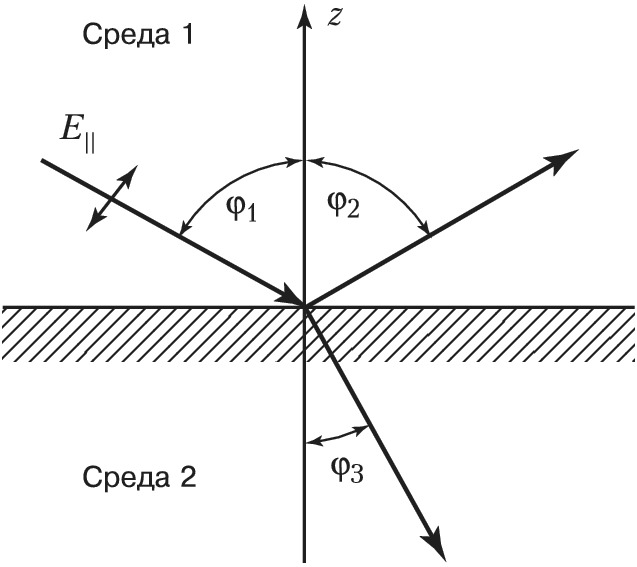
При па­де­нии пло­ской све­то­вой вол­ны под уг­лом $φ_1$ на гра­ни­цу раз­де­ла двух про­зрач­ных сред об­ра­зу­ют­ся от­ра­жён­ная вол­на под уг­лом $φ_2$ и пре­лом­лён­ная вол­на под уг­лом $φ_3$ (рис.). Ес­ли век­тор элек­трич. по­ля $\boldsymbol E$ вол­ны ле­жит в плос­ко­сти па­де­ния и нор­ма­ли к гра­ни­це раз­де­ла сред (по­ля­ри­за­ция в плос­ко­сти па­де­ния, $E≡E_{||}$), то ам­пли­туд­ный ко­эф. от­ра­же­ния ра­вен $r_{||}=\text{tg}(φ_1-φ_3)/\text{tg}(φ_1+φ_3)$. Ес­ли век­тор $\boldsymbol E$ пер­пен­ди­ку­ля­рен плос­ко­сти па­де­ния, то $r_{⊥}=-\sin(φ_1-φ_3)/\sin(φ_1+φ_3)$. Знак ми­нус пе­ред ко­эф. от­ра­же­ния оз­на­ча­ет, что при от­ра­же­нии от бо­лее плот­ной сре­ды (с бо́ль­шим по­ка­за­те­лем пре­лом­ле­ния) к фа­зе от­ра­жён­ной вол­ны до­бав­ля­ет­ся сдвиг на $π$ по от­но­ше­нию к фа­зе па­даю­щей вол­ны. Фа­за пре­лом­лён­ной вол­ны все­гда рав­на фа­зе па­даю­щей.

Со­стоя­ние по­ля­ри­за­ции при от­ра­же­нии и пре­лом­ле­нии в об­щем слу­чае из­ме­ня­ет­ся. При па­де­нии под уг­лом Брю­сте­ра ($r_{||}=0$) от­ра­жён­ная вол­на пол­но­стью по­ля­ри­зо­ва­на (см. Брю­сте­ра за­кон

).

При пол­ном внут­рен­нем от­ра­же­нии

ам­пли­ту­да про­шед­шей вол­ны экс­по­нен­ци­аль­но за­ту­ха­ет с ха­рак­тер­ной глу­би­ной про­ник­но­ве­ния (см. На­ру­шен­ное пол­ное внут­рен­нее от­ра­же­ние

 >>

), а ко­эф. от­ра­же­ния ра­вен еди­ни­це.

Ф. ф. спра­вед­ли­вы в слу­чае глад­кой гра­ни­цы раз­де­ла двух изо­троп­ных про­зрач­ных ди­элек­три­ков, ко­гда угол от­ра­же­ния ра­вен уг­лу па­де­ния, а угол пре­лом­ле­ния оп­ре­де­ля­ет­ся Снел­ла за­ко­ном

. Для не­ров­ной по­верх­но­сти с ха­рак­тер­ны­ми раз­ме­ра­ми не­ров­но­стей по­ряд­ка дли­ны вол­ны пре­об­ла­да­ет диф­фуз­ное от­ра­же­ние. Ф. ф. при­ме­ня­ют­ся в ли­ней­ной оп­ти­ке, ко­гда по­ка­за­те­ли пре­лом­ле­ния сред не за­ви­сят от ин­тен­сив­но­сти све­та. В не­ли­ней­ной оп­ти­ке и для ме­та­ма­те­риа­лов

 >>

они не вы­пол­ня­ют­ся.