НАРУ́ШЕННОЕ ПО́ЛНОЕ ВНУ́ТРЕННЕЕ ОТРАЖЕ́НИЕ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
НАРУ́ШЕННОЕ ПО́ЛНОЕ ВНУ́ТРЕННЕЕ ОТРАЖЕ́НИЕ (НПВО), частичное проникновение электромагнитного излучения (в частности, света или радиоволн) из оптически плотной среды 1 с показателем преломления $n_1$ в слой конечной толщины $D$ граничащей с ней менее плотной среды 2 с показателем преломления $n_2$ в условиях полного внутреннего отражения (ПВО) на границе сред ($n_1>n_2$). Если показатели преломления сред не зависят от длины волны излучения, то необходимое условие ПВО выполняется при наклонном падении излучения под достаточно большим углом $γ$ к нормали к границе сред: $γ>γ_{\text{кр}}$ (критич. угол $γ_{\text{кр}}$ определяется из условия $\text{sin}\gamma_{\text{кр}}=n_2/n_1$).
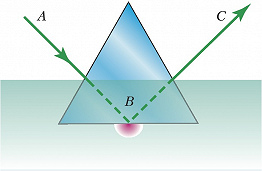
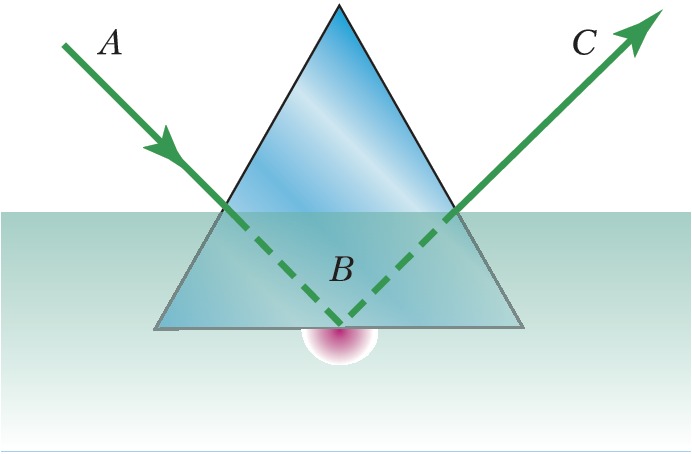
В 1908 рос. физик А. А. Эйхенвальд впервые теоретически показал, что даже при выполнении этого условия падающая волна не обрывается на границе сред, а частично проникает в прозрачную среду 2; при этом её амплитуда ослабевает экспоненциально внутри среды 2 на глубине $d$, равной нескольким длинам волн. Это затухание, никак не связанное с поглощением волны, имеет волновую природу и не может быть описано как «отражение лучей» в геометрич. оптике. Этот вывод вскоре был подтверждён опытом Л. И. Мандельштама и П. Селени (рис. 1). Свет падает через боковую стенку призмы в направлении $AB$ на её нижнюю грань, погружённую во флуоресцирующую жидкость, под углом, бо́льшим, чем угол ПВО $γ_{\text{кр}}$. Отражённый свет распространяется в направлении $BC$. В тонком слое жидкости, прилегающем к нижней грани призмы, видно свечение флуоресценции, ослабевающее в глубине жидкости.
Эффект НПВО наблюдается, если толщина $D$ соизмерима с глубиной затухания $d$; при этом внутр. отражение волны становится неполным, часть энергии волны проходит через слой, нарушая ПВО. Нарушения ПВО не видно, если $D≫d$.
НПВО может наблюдаться и при нормальном падении, если $n_2$ зависит от частоты волны (дисперсия света). Так, при нормальном падении волны с частотой $ω$ на плоский слой газовой плазмы толщиной $d$, показатель преломления которой $n=(1-ω^2_{\text{пл}}/ω^2)^{1/2}$ ($ω_{\text{пл}}$ – плазменная частота, зависящая от плотности плазмы), слой прозрачен лишь для частот выше плазменной ($ω>ω_{\text{пл}}$). Для частот меньше $ω_{\text{пл}}$ показатель преломления становится мнимой величиной, и волны с частотой $ω<ω_{\text{пл}}$ не проходят через плазму, а полностью отражаются; однако при соответствующих значениях параметров $d$ и $D$ возможно возникновение НПВО. В частности, эффект НПВО приводит к частичному просачиванию (туннелированию) радиоволн через плотные слои ионосферной плазмы. Эффект НПВО в микроскопии ближнего поля позволяет понять, как информация о субволнах передаётся в дальнее поле. Методы НПВО широко используются при изучении поверхностных электромагнитных волн, структуры тонких слоёв, абсорбционных явлений и др.
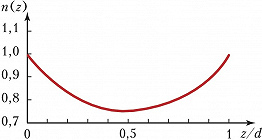
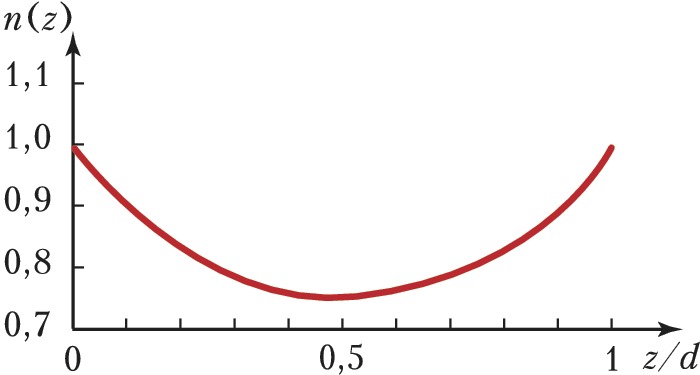
В связи с появлением градиентных наноматериалов интересен особый случай НПВО – безотражательное туннелирование для частот $ω<ω_{\text{пл}}$, при котором энергия электромагнитной волны эффективно переносится через плёнку диэлектрика, показатель преломления которой распределён поперёк слоя по определённому закону (рис. 2). Для такой градиентной плёнки, созданной с помощью нанотехнологии, возникает т. н. частота отсечки $Ω$, определяемая толщиной слоя $d$ и профилем показателя преломления; при толщинах порядка 100 нм частота $Ω$ лежит в области видимых и ближних ИК-частот. Для некоторых волн с частотой $ω<Ω$ , которые формально не могут пройти через плёнку, в результате интерференции отражённых от границ слоя волн происходит гашение отражённого сигнала, приводящее к эффекту НПВО с безотражательным переносом до 100% энергии волны. Такие наноплёнки толщиной в неск. раз меньше длины волны представляют интерес для создания миниатюрных поляризаторов, частотных фильтров и безотражательных покрытий.
Эффекты НПВО возможны и для волн др. физич. природы, напр. для звука в диспергирующих средах.