РАЗМЕ́РНЫЕ ЭФФЕ́КТЫ

РАЗМЕ́РНЫЕ ЭФФЕ́КТЫ, на­блю­да­ют­ся в ус­ло­ви­ях, ко­гда гео­мет­рич. раз­ме­ры объ­ек­та срав­ни­мы с од­ной из длин, оп­ре­де­ляю­щих про­те­ка­ние фи­зи­ко-хи­мич. про­цес­сов (напр., дли­ной сво­бод­но­го про­бе­га но­си­те­ля за­ря­да, дли­ной вол­ны де Брой­ля). Раз­ли­ча­ют клас­сич. и кван­то­вые Р. э. Пер­вые про­яв­ля­ют­ся, напр., в за­ви­си­мо­сти ки­не­тич. ко­эф­фи­ци­ен­тов (элек­тро­про­вод­но­сти, те­п­ло­про­вод­но­сти и др.) тон­ких ме­тал­лич. и по­лу­про­вод­ни­ко­вых плё­нок, про­во­лок, ни­те­вид­ных кри­стал­лов от од­но­го из гео­мет­рич. раз­ме­ров d, ко­гда он со­из­ме­рим с дли­ной сво­бод­но­го про­бе­га l ква­зи­ча­стиц (элек­тро­нов про­во­ди­мо­сти, фо­но­нов, маг­но­нов и др.). Так, при умень­ше­нии d удель­ное элек­трич. со­про­тив­ле­ние мо­но­тон­но воз­рас­та­ет, что обу­слов­ле­но до­пол­нит. рас­сея­ни­ем ква­зи­ча­стиц гра­ни­цей об­раз­ца. Р. э. мо­гут воз­ни­кать во внеш­нем силь­ном маг­нит­ном по­ле, ко­гда d срав­ним с раз­ме­ра­ми ор­би­ты элек­тро­нов про­во­ди­мо­сти в этом по­ле.

Зависимость удельного электрического сопротивления ρ плёнок Вi от толщины d при различных температурах Т. С ростом d и Т осцилляции затухают.

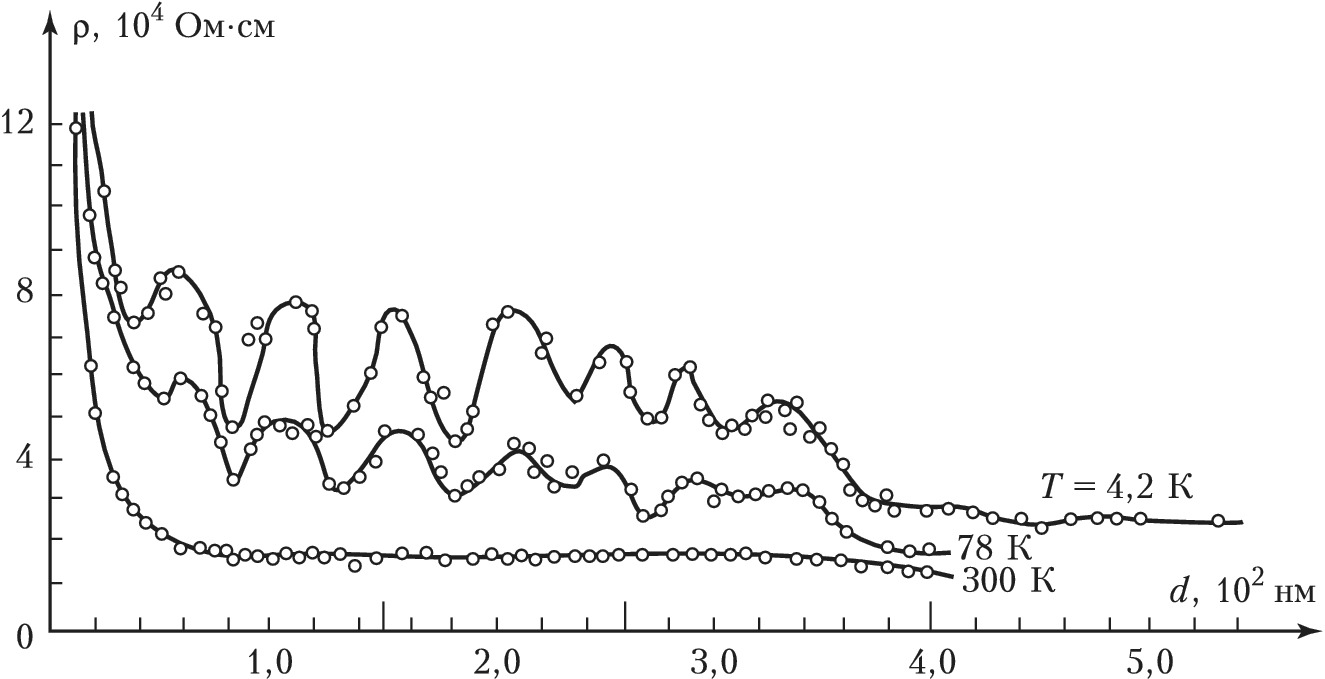
Кван­то­вые Р. э. воз­ни­ка­ют, ко­гда d со­из­ме­рим с дли­ной вол­ны де Брой­ля λ_Б элек­тро­на. Они обу­слов­ле­ны кван­то­ва­ни­ем дви­же­ния элек­тро­на в на­прав­ле­нии, в ко­то­ром d срав­ним с λ_Б (т. н. раз­мер­ное кван­то­ва­ние). В мас­сив­ном иде­аль­ном кри­стал­ле со­стоя­ние элек­тро­на оп­ре­де­ля­ет­ся за­да­ни­ем че­ты­рёх кван­то­вых чи­сел: n – но­ме­ра энер­ге­тич. зо­ны и трёх про­ек­ций его ква­зи­им­пуль­са р на ко­ор­ди­нат­ные оси (p_x, p_y, p_z), ко­то­рые мо­гут при­нимать лю­бые зна­че­ния. В кри­стал­лич. плён­ке тол­щи­ной d, нор­маль к ко­то­рой на­прав­ле­на по оси z, дви­же­ние элек­тро­на в плос­ко­сти плён­ки ос­та­ёт­ся сво­бод­ным, т. е. p_x и p_y мо­гут при­ни­мать лю­бые зна­че­ния. Ве­ли­чи­на p_z мо­жет при­ни­мать толь­ко дис­крет­ный ряд зна­че­ний, что свя­за­но с тем, что вол­но­вая функ­ция элек­тро­на на по­верх­но­стях плён­ки долж­на об­ра­щать­ся в 0. Это оз­на­ча­ет, что на тол­щи­не d долж­но ук­ла­ды­вать­ся це­лое чис­ло n=1, 2,... по­лу­волн де Брой­ля: λ_Б/2=pℏ/|p_z|. От­сю­да сле­ду­ет кван­то­ва­ние про­ек­ции ква­зи­им­пуль­са p_z и энер­гии ℰ_n по­пе­реч­но­го дви­же­ния элек­тро­на. Раз­мер­ное кван­то­ва­ние при­во­дит к ра­ди­каль­ной пе­ре­строй­ке плот­но­сти элек­трон­ных со­стоя­ний g(ℰ). В мас­сив­ном кри­стал­ле g(ℰ) име­ет плав­ный мо­но­тон­ный ха­рак­тер, и, сле­до­ва­тель­но, элек­трон­ные свой­ст­ва под влия­ни­ем внеш­них воз­дей­ст­вий из­ме­ня­ют­ся пре­им. плав­но. В тон­кой плён­ке плот­ность со­стоя­ний яв­ля­ет­ся сту­пен­ча­той функ­ци­ей энер­гии, и её скач­ко­об­раз­ное из­ме­не­ние долж­но при­во­дить к ос­цил­ли­рую­щей за­ви­симо­сти от d ря­да фи­зич. па­ра­мет­ров, напр. удель­но­го элек­трич. со­про­тив­ле­ния (рис.), кон­стан­ты Хол­ла (см. Кван­то­вый эф­фект Хол­ла) и маг­ни­то­со­про­тив­ле­ния (см. Галь­ва­но­маг­нит­ные яв­ле­ния), а так­же к осо­бен­но­стям фи­зич. свойств плё­нок Pb, Mg, Au, Ag, обу­слов­лен­ных тун­не­ли­ро­ва­ни­ем элек­тро­нов.

Р. э. на­блю­да­ют­ся в ма­те­риа­лах и сис­те­мах, со­стоя­щих из час­тиц, раз­ме­ры ко­то­рых не пре­вы­ша­ют 100 нм (см. Нано­ст­рук­ту­ры). К осн. кван­то­во­раз­мер­ным струк­ту­рам от­но­сят­ся струк­ту­ры с дву­мер­ным элек­трон­ным га­зом (эпи­так­си­аль­ные плён­ки, МДП-струк­ту­ры, ге­те­ро­ст­рук­ту­ры), струк­ту­ры с од­но­мер­ным га­зом (кван­то­вые про­во­ло­ки), струк­ту­ры с нуль­мер­ным га­зом (кван­то­вые точ­ки).