КВА́НТОВЫЙ ЭФФЕ́КТ ХО́ЛЛА

Рис. 1. Пример зависимостей ρхх и ρху от напряжённости магнитного поля Н для целочисленного квантового эффекта Холла.

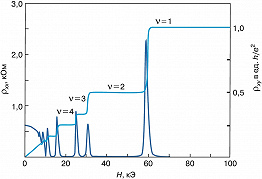
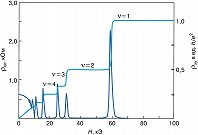
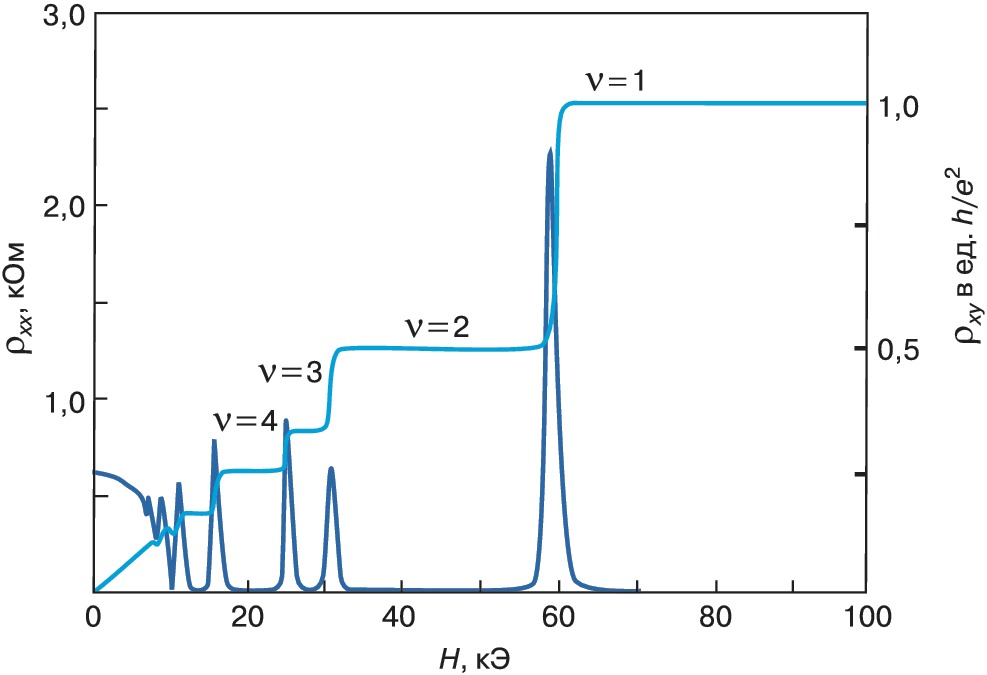
КВА́НТОВЫЙ ЭФФЕ́КТ ХО́ЛЛА, мак­ро­ско­пич. кван­то­вый эф­фект, про­яв­ляю­щий­ся в кван­то­ва­нии хол­лов­ско­го со­про­тив­ле­ния $\rho_{xy}$ (см. Хол­ла эф­фект) и ис­чез­но­ве­нии удель­но­го со­про­тив­ле­ния $\rho_{xx}$. К. э. X. на­блю­да­ет­ся при низ­ких темп-pax $T$ в дву­мер­ном слое но­си­те­лей за­ря­да в по­лу­про­вод­ни­ках, по­ме­щён­ных в маг­нит­ное по­ле на­пря­жён­но­стью $\boldsymbol H$, пер­пен­ди­ку­ляр­ной плос­ко­сти $xy$. В от­ли­чие от клас­сич. эф­фек­та Хол­ла, при ко­то­ром $\rho_{xy}$ мо­но­тон­но за­ви­сит от $H$ или кон­цен­тра­ции но­си­те­лей за­ря­да $n$ ($\rho_{xy}=H/nec$, где $e$ – за­ряд элек­тро­на, $c$ – ско­рость све­та), в слу­чае К. э. X. $\rho_{xy}$ при­ни­ма­ет дис­крет­ные зна­че­ния, а ком­по­нен­та $\rho_{xx}$ ста­но­вит­ся ис­че­заю­ще ма­лой по срав­не­нию со сво­им зна­че­ни­ем при $H=0$: $$\rho_{xy}=(2\pi \hbar)/(\nu e^2),\\ \rho_{xx} \to 0. \quad\tag{1}$$Здесь $2 \pi \hbar/e^2=25812,8$ Ом, $\hbar$ – по­сто­ян­ная План­ка, $\nu=p/q$ – це­лые или дроб­ные ра­цио­наль­ные чис­ла ($p$, $q$ – це­лые чис­ла). Со­от­но­ше­ния (1) вы­пол­ня­ют­ся для ря­да ин­тер­ва­лов кон­цен­тра­ции но­си­те­лей за­ря­да $n$ при по­сто­ян­ном $H$ или для ря­да ин­тер­ва­лов $H$ при по­сто­ян­ной кон­це­нт­ра­ции $n$ (рис. 1).

К. э. X. с це­ло­чис­лен­ны­ми $\nu=1,2,\dots$ (це­ло­чис­лен­ный К. э. X.) от­крыт К. фон Клит­цин­гом в 1980. К. э. X. с дроб­ны­ми $\nu=$¹/₃, ²/₃, ⁴/₃, ⁵/₃, ⁷/₃, ⁸/₃, ¹/₅, ²/₅, ³/₅, ⁴/₅ и т. д. (дроб­ный К. э. X.) от­крыт Д. Цуи и X. Стор­ме­ром в 1982. К. э. X. на­блю­да­ет­ся в дву­мер­ных сло­ях $n$- и $p$-ти­па в крем­ние­вых МДП-струк­ту­рах (ме­талл – ди­элек­трик – по­лу­про­вод­ник), а так­же в ге­те­ро­пе­ре­хо­дах GaAs/AlGaAs, Si/SiGe и др. в силь­ных маг­нит­ных по­лях и при низ­ких темп-pax $T \ll \hbar \omega_c$ ($\omega_c=eH/m^*c$ – цик­ло­трон­ная час­то­та, $m^*$ – эф­фек­тив­ная мас­са элек­тро­на). При по­вы­ше­нии темп-ры уве­ли­чи­ва­ет­ся со­про­тив­ле­ние в ми­ни­му­ме $\rho_{xx}$, умень­ша­ет­ся ши­ри­на пла­то $\rho_{xy}$ и уве­ли­чи­ва­ет­ся его на­клон.

Ком­по­нен­ты $\rho_{xy}$ и $\rho_{xx}$ тен­зо­ра со­про­тив­ле­ния из­ме­ря­ют на пря­мо­уголь­ных об­раз­цах с че­тырь­мя или бо­лее кон­так­та­ми к ин­вер­си­он­но­му слою, про­пус­кая по­сто­ян­ный или пе­ре­мен­ный ток $I_x$. Раз­ность по­тен­циа­лов ме­ж­ду кон­так­та­ми – вдоль то­ка $V_x$ и по­пе­рёк то­ка $V_y$ – по­зво­ля­ет оп­ре­де­лить ком­по­нен­ты тен­зо­ра удель­но­го cопротивления $\rho$ и про­во­ди­мо­сти $\sigma$: $$\rho_{xx}=W/L(V_x/I_x);\\ \rho_{xy}=V_y/I_x;\\ \sigma_{xx}=\rho_{xx}/(\rho_{xx}^2+\rho_{xy}^2);\\ \sigma_{xy}=\rho_{xy}/(\rho_{xx}^2+\rho_{xy}^2). \quad\tag{2}$$Здесь $W$ – ши­ри­на дву­мер­но­го слоя, $L$ – рас­стоя­ние ме­ж­ду кон­так­та­ми вдоль то­ка. Вид­но, что $\rho_{xx} \to0$ и $\sigma_{xx} \to 0$ од­но­вре­мен­но, в то вре­мя как хол­лов­ская ком­по­нен­та про­во­ди­мо­сти $\sigma_{xy} \to 1/\rho_{xy}$ и так­же яв­ля­ет­ся кван­то­ван­ной ве­ли­чи­ной.

Це­ло­чис­лен­ный К. э. X. объ­яс­ня­ет­ся на ос­но­ве од­но­час­тич­ных пред­став­ле­ний (не­взаи­мо­дей­ст­вую­щие элек­тро­ны); но­си­те­ли за­ря­да рас­смат­ри­ва­ют­ся как дву­мер­ный элек­трон­ный газ. В маг­нит­ном по­ле на­пря­жён­но­стью $\boldsymbol H$, пер­пен­ди­ку­ляр­ной плос­ко­сти слоя, энер­ге­тич. спектр элек­тро­нов из не­пре­рыв­но­го ста­но­вит­ся дис­крет­ным. При дос­та­точ­ной ве­ли­чи­не $H$ спектр со­сто­ит из отд. эк­ви­ди­стантных не­пе­ре­кры­ваю­щих­ся Лан­дау уров­ней. Энер­гия $j$-го уров­ня $$\mathscr E_j=(j+1/2)\hbar \omega_c, j=0,1,2,\dots \quad\tag{3}$$Плот­ность раз­ре­шён­ных со­стоя­ний на ка­ж­дом из уров­ней Лан­дау $n_H$ рав­на плот­но­сти кван­тов маг­нит­но­го по­то­ка Φ, про­ни­зы­ваю­ще­го дву­мер­ный слой: $$n_H=Ф/Ф_0=eH(2\pi \hbar c),\quad\tag{4}$$где $Ф_0=2\pi \hbar c/e$ – квант маг­нит­но­го по­тока.

Рис. 2. Связь между плотностью состояний g(ℰ) для двумерной системы и зависимостью σxx и σху от концентрации электронов n/nH; ℰF – уровень Ферми.

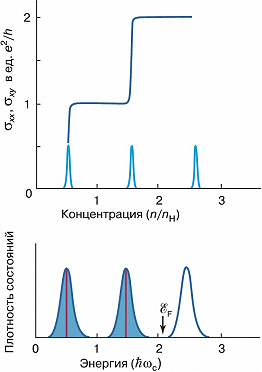
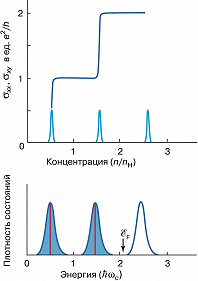
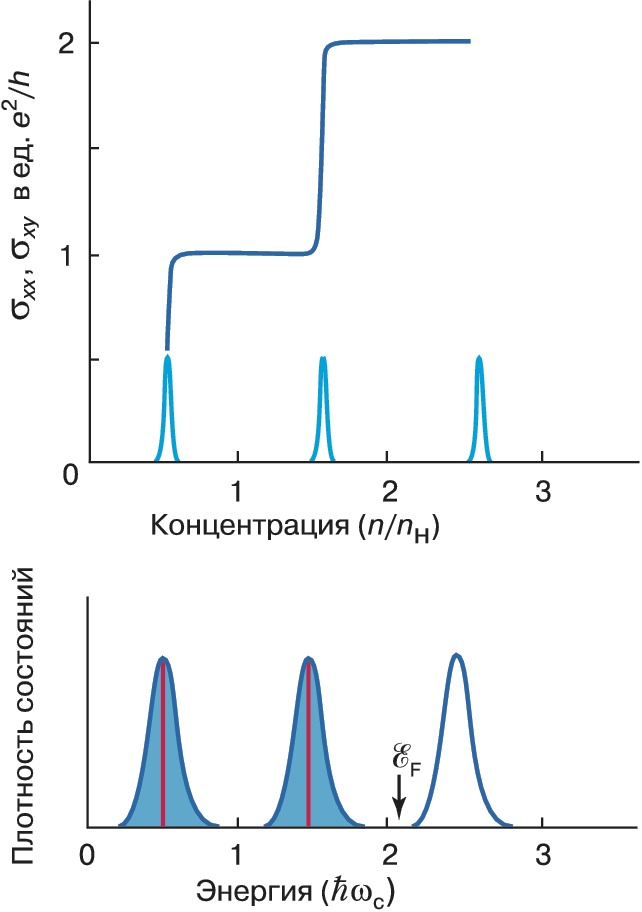
При из­ме­не­нии кон­цен­тра­ции но­си­те­лей $n$ в слое или на­пря­жён­но­сти $H$ маг­нит­но­го по­ля из­ме­ня­ет­ся по­ло­же­ние уров­ня Фер­ми $\mathscr E_F$ от­но­си­тель­но сис­те­мы уров­ней Лан­дау. Ес­ли $\mathscr E_F$ на­хо­дит­ся в об­лас­ти ме­ж­ду дву­мя со­сед­ни­ми уров­ня­ми Лан­дау $(j,j+1)$, где энер­ге­тич. плот­ность со­стоя­ний $g(\mathscr E)$ ма­ла, то при $T \to 0$ все со­стоя­ния на уров­нях Лан­дау, ле­жа­щих ни­же уров­ня $j$, пол­но­стью за­пол­не­ны. Это­му ус­ло­вию от­ве­ча­ет кон­цен­тра­ция но­си­те­лей, рав­ная $$n=jn_H=jeH/(2\pi \hbar c). \quad\tag{5}$$Под­ста­нов­ка (5) в фор­му­лу для обыч­ного эф­фек­та Хол­ла да­ёт со­от­но­ше­ние (1) с це­ло­чис­лен­ным зна­че­ни­ем $\nu=j=n/n_H$, имею­щим смысл при­ве­дён­ной кон­цен­т­ра­ции. Т. о., се­ре­ди­нам пла­то $\rho_{xy}$ со­от­вет­ст­ву­ет рас­по­ло­же­ние $\mathscr E_F$ по­се­ре­ди­не ме­ж­ду уров­ня­ми Лан­дау, а пе­ре­ход­ный уча­сток ме­ж­ду дву­мя со­сед­ни­ми пла­то со­от­вет­ст­ву­ет на­хо­ж­де­нию $\mathscr E_F$ в об­лас­ти мак­си­му­ма $g(\mathscr E)$, т. е. в цен­тре уров­ня Лан­дау (рис. 2).

Ши­ро­кие пла­то $\rho_{xy}$ и ми­ни­му­мы $\rho_{xx}$ свя­за­ны с су­ще­ст­во­ва­ни­ем на «крыль­ях» уров­ней Лан­дау ло­ка­ли­зо­ван­ных со­сто­я­ний элек­тро­нов. В про­во­ди­мо­сти уча­ст­ву­ют лишь де­ло­ка­ли­зо­ван­ные но­си­те­ли за­ря­да, ко­то­рые за­ни­ма­ют уз­кую по энер­гии по­лос­ку в се­ре­ди­нах уров­ней Лан­дау (рис. 2). Наи­бо­лее рас­про­стра­нён­ный ме­ха­низм воз­ник­но­ве­ния свя­зан­ных со­стоя­ний – ло­ка­ли­за­ция элек­тро­нов на флук­туа­ци­ях по­тен­циа­ла, ана­ло­гич­ная ан­дер­со­нов­ской ло­ка­ли­за­ции при от­сут­ст­вии маг­нит­но­го по­ля. Рис. 2 по­яс­ня­ет по­ве­де­ние $\sigma_{xx}$ и $\sigma_{xy}$ при из­ме­не­нии $n$ или $H$. Ко­гда $\mathscr E_F$ рас­по­ло­же­на в об­лас­ти ло­ка­ли­зо­ван­ных со­стоя­ний на кры­ле $j$-го уров­ня, то ло­ка­ли­зо­ван­ные но­си­те­ли не уча­ст­ву­ют в элек­тро­про­вод­но­сти и весь ток про­те­ка­ет толь­ко по об­лас­тям де­ло­ка­ли­зо­ван­ных со­стоя­ний. Т. к. эти со­стоя­ния рас­по­ло­же­ны по энер­гии ни­же $\mathscr E_F$, то кон­цен­тра­ция но­си­те­лей $n$ в них мак­си­маль­но воз­мож­ная (5) и $\rho_{xy}$ име­ет кван­то­ван­ное зна­че­ние (1). При уве­ли­че­нии $n$ до­бав­ляе­мые в дву­мер­ный слой но­вые но­си­те­ли за­ря­да по­па­да­ют в об­лас­ти ло­ка­ли­зо­ван­ных но­си­те­лей. Кон­цен­тра­ция де­ло­ка­ли­зо­ван­ных но­си­те­лей при этом не из­ме­ня­ет­ся и, сле­до­ва­тель­но, не из­ме­ня­ет­ся зна­че­ние $\rho_{xy}$. Так про­дол­жа­ет­ся до тех пор, по­ка $\mathscr E_F$ не вый­дет за пре­де­лы об­лас­ти ло­ка­ли­зо­ван­ных со­стоя­ний и не по­па­дёт в об­ласть де­ло­ка­ли­зо­ван­ных со­стоя­ний на $j+1$ уро­вень. При этом кон­цен­тра­ция де­ло­ка­ли­зо­ван­ных но­си­те­лей нач­нёт из­ме­нять­ся со­от­вет­ст­вен­но из­ме­не­нию $\mathscr E_F$; это­му со­от­вет­ст­ву­ет пе­ре­ход­ный уча­сток ме­ж­ду дву­мя со­сед­ни­ми пла­то $\sigma_{xy}$ (рис. 2). Т. о., со­от­но­ше­ние (1) вы­пол­ня­ет­ся в ин­тер­ва­ле энер­гий, рав­ном ще­ли в спек­тре де­ло­ка­ли­зо­ван­ных со­стоя­ний.

Не­обыч­ные мо­ди­фи­ка­ции К. э. X. на­блю­да­ют­ся в трёх­мер­ных ор­га­нич. ма­те­риа­лах с рез­ко ани­зо­троп­ной про­во­ди­мо­стью (в фа­зе вол­ны спи­но­вой плот­но­сти) и в гра­фе­не (мо­но­атом­ные слои гра­фи­та). В пер­вом слу­чае уро­вень Фер­ми мо­жет на­хо­дить­ся толь­ко в об­лас­ти энер­ге­тич. ще­лей, и по­это­му пе­ре­хо­ды ме­ж­ду пла­то яв­ля­ют­ся скач­ко­об­раз­ны­ми фа­зо­вы­ми пе­ре­хо­да­ми 1-го ро­да. В гра­фе­не, вви­ду бес­ще­ле­во­го ли­ней­но­го спек­тра но­си­те­лей за­ря­да, по­ло­же­ния пла­то сдви­ну­ты на ¹/₂ от це­ло­чис­лен­ных фак­то­ров за­пол­не­ния (1), а ве­ли­чи­на энер­ге­тич. ще­ли ока­зы­ва­ет­ся столь ве­ли­ка, что К. э. X. на­блю­да­ет­ся вплоть до ком­нат­ных темп-р.

Дроб­ный К. э. X. яв­ля­ет­ся су­гу­бо мно­го­час­тич­ным эф­фек­том, след­ст­ви­ем силь­но­го ку­ло­нов­ско­го взаи­мо­дей­ст­вия и кор­ре­ля­ций ме­ж­ду ква­зи­ча­сти­ца­ми.

Для на­блю­де­ния К. э. X. по­ми­мо низ­ких темп-р и силь­ных маг­нит­ных по­лей не­об­хо­ди­мы об­раз­цы с дос­та­точ­но вы­со­кой под­виж­но­стью но­си­те­лей за­ря­да (т. е. с ма­лой ши­ри­ной уров­ней Лан­дау).

На ос­но­ве це­ло­чис­лен­но­го К. э. Х. осу­ще­ст­в­ля­ет­ся вос­про­из­ве­де­ние еди­ни­цы элек­трич. со­про­тив­ле­ния (ом).