ПЛА́НКА ЗАКО́Н ИЗЛУЧЕ́НИЯ

ПЛА́НКА ЗАКО́Н ИЗЛУЧЕ́НИЯ, опи­сы­ва­ет спек­траль­ное рас­пре­де­ле­ние энер­гии элек­тро­маг­нит­но­го из­лу­че­ния, на­хо­дя­ще­го­ся в те­п­ло­вом рав­но­ве­сии с ве­ще­ст­вом при за­дан­ной тем­пе­ра­ту­ре. Идеа­ли­зи­ро­ван­ной мо­де­лью рав­но­вес­но­го из­лу­че­ния слу­жит элек­тро­маг­нит­ное по­ле внут­ри по­лос­ти, рас­по­ло­жен­ной в на­гре­том ве­ще­ст­ве, при ус­ло­вии, что стен­ки ве­ще­ст­ва не­про­зрач­ны для из­лу­че­ния. Спектр та­ко­го рав­но­вес­но­го из­лу­че­ния на­зы­ва­ют спек­тром из­лу­че­ния аб­со­лют­но чёр­но­го те­ла

. Объ­ём­ная плот­ность энер­гии из­лу­че­ния $u_ω$, при­хо­дя­щей­ся на еди­нич­ный ин­тер­вал час­тот $ω$, вы­ра­жа­ет­ся т. н. фор­му­лой План­ка: $$u_ω=\frac{ω^2}{π^2 c^2}\cdot\frac{\hbar ω}{e^{\hbar ω/kT}-1},$$ где $T$ – аб­со­лют­ная темп-ра, $k$ – по­сто­ян­ная Больц­ма­на, $c$ – ско­рость све­та, $\hbar$  – по­сто­ян­ная План­ка. Т. о., по спек­тру из­лу­че­ния аб­со­лют­но чёр­но­го те­ла мож­но оп­ре­де­лить его тер­мо­ди­на­мич. темп-ру. Эта фор­му­ла бы­ла вы­ве­де­на М. План­ком

 >>

в 1900 в ре­зуль­та­те рас­смот­ре­ния ба­лан­са об­ме­на энер­ги­ей ме­ж­ду дву­мя ви­да­ми ос­цил­ля­то­ров: час­ти­ца­ми ве­ще­ст­ва, по­гло­щаю­щи­ми и ис­пус­каю­щи­ми из­лу­че­ние на час­то­те $ω$, и ос­цил­ля­то­ра­ми, пред­став­ляю­щи­ми элек­тро­маг­нит­ное по­ле той же час­то­ты. Планк пред­по­ло­жил, что та­кие ос­цил­ля­то­ры мо­гут на­хо­дить­ся толь­ко в со­стоя­ни­ях с дис­крет­ной энер­ги­ей и об­ме­ни­ва­ют­ся ме­ж­ду со­бой кван­та­ми энер­гии ве­ли­чи­ной $Δ\mathscr {E}=\hbar ω$. Зна­че­ние ко­эф. про­пор­цио­наль­но­сти $\hbar$ ме­ж­ду час­то­той ос­цил­ля­то­ра и ве­ли­чи­ной кван­та энер­гии Планк ус­та­но­вил ис­хо­дя из экс­пе­рим. дан­ных: $\hbar$=1,054·10^–34 Дж·с. Пред­по­ло­же­ние о дис­крет­ном на­бо­ре воз­мож­ных зна­че­ний энер­гии ос­цил­ля­то­ров по­ля ($0, \hbar ω, 2\hbar ω, 3\hbar ω, ...$) ста­ло впо­след­ст­вии ос­но­ва­ни­ем для вве­де­ния по­ня­тия кван­та элек­тро­маг­нит­но­го из­лу­че­ния (фо­то­на

 >>

).

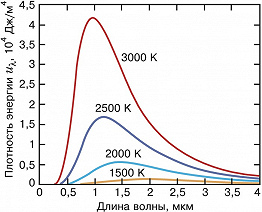
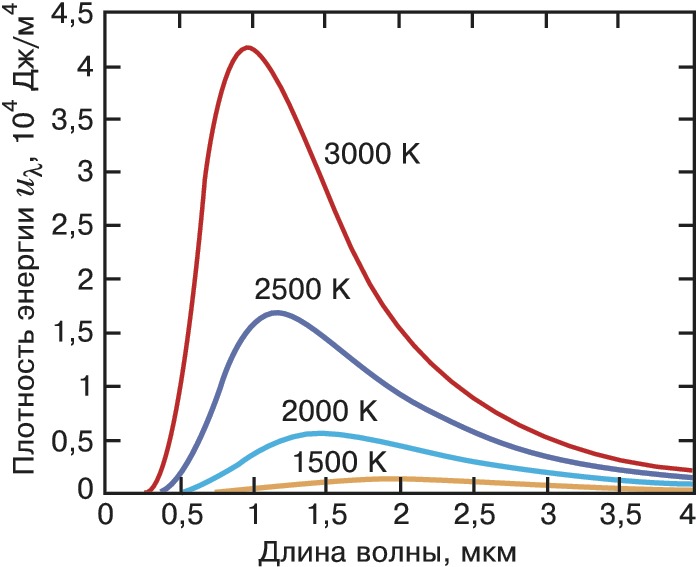
Спек­траль­ная плот­ность энер­гии мо­жет быть рас­счи­та­на так­же для др. ха­рак­те­ри­стик из­лу­че­ния – час­то­ты $ν=ω/2π$ или дли­ны вол­ны $λ=c/ν= 2πc/ω$. То­гда фор­му­ла План­ка при­об­ре­та­ет вид (здесь $h=2π\hbar$): $$u_v=\frac{8πhv^3}{c^3}\cdot\frac{1}{e^{hv/kT}-1}$$ или $$u_λ=\frac{8πhc}{λ^5}\cdot\frac{1}{e^{hc/λkT}-1}.$$ За­ви­си­мость спек­траль­ной плот­но­сти энер­гии от дли­ны вол­ны из­лу­че­ния пред­став­ле­на на ри­сун­ке.

Для вы­во­да фор­му­лы План­ка не­об­хо­дим под­счёт чис­ла ос­цил­ля­то­ров из­лу­че­ния, при­хо­дя­щих­ся на еди­нич­ный ин­тер­вал час­тот; эта ве­ли­чи­на для еди­нич­но­го объ­ё­ма со­став­ля­ет $ω/π^2c^3$. Ес­ли при­нять, что ср. энер­гия ос­цил­ля­то­ра по­ля рав­на $kT$, как это сле­ду­ет из Больц­ма­на рас­пре­де­ле­ния

 для не­пре­рыв­но­го на­бо­ра воз­мож­ных зна­че­ний энер­гии, то для плот­но­сти энер­гии из­лу­че­ния $u_ω$ по­лу­чит­ся фор­му­ла Рэ­лея – Джин­са (см. Рэ­лея – Джин­са за­кон из­лу­че­ния

 >>

): $$u_ω=\frac{ω^2}{π^2 c^3}\cdot kT.$$ Фор­му­ла Рэ­лея – Джин­са при­ме­ни­ма толь­ко для ма­лых час­тот ($\hbar ω≪kT$), т. к. она пред­ска­зы­ва­ет не­ог­ра­ни­чен­ный рост плот­но­сти энер­гии, а зна­чит, и пол­ной энер­гии из­лу­че­ния, с рос­том час­то­ты (т. н. ульт­ра­фио­ле­то­вая ка­та­ст­ро­фа), что на­хо­дит­ся в про­ти­во­ре­чии с экс­пе­рим. дан­ны­ми. Имен­но для сня­тия это­го про­ти­во­ре­чия М. Планк вы­дви­нул пред­по­ло­же­ние о дис­крет­ном на­бо­ре энер­гий ос­цил­ля­то­ра элек­тро­маг­нит­но­го по­ля; по­лу­чен­ная им фор­му­ла хо­ро­шо со­гла­су­ет­ся с экс­пе­рим. дан­ны­ми.

Фор­му­ла План­ка кон­кре­ти­зи­ру­ет весь­ма об­щее со­от­но­ше­ние для плот­но­сти энер­гии рав­но­вес­но­го из­лу­че­ния, ус­та­нов­лен­ное В. Ви­ном

(см. Ви­на за­кон сме­ще­ния

 >>

), и со­гла­су­ет­ся с ус­та­нов­лен­ным ра­нее Сте­фа­на – Больц­ма­на за­коном из­лу­че­ния

 >>

, ут­вер­ждаю­щим, что пол­ная (по всем час­то­там) плот­ность энер­гии про­пор­цио­наль­на чет­вёр­той сте­пе­ни темп-ры.

Хо­тя фор­му­ла План­ка вы­ве­де­на для опи­са­ния рав­но­вес­но­го из­лу­че­ния в по­лос­ти на­гре­то­го ве­ще­ст­ва, она ока­зы­ва­ет­ся при­год­ной и для опи­са­ния спек­траль­но­го рас­пре­де­ле­ния лу­чи­стой энер­гии, ис­пус­кае­мой ре­аль­ны­ми те­ла­ми в ок­ру­жаю­щее про­стран­ст­во. Ре­ги­ст­ра­ция спек­тров из­лу­че­ния звёзд и их со­пос­тав­ле­ние с фор­му­лой План­ка яв­ля­ет­ся осн. ме­то­дом ус­та­нов­ле­ния темп-ры их по­верх­но­сти. Этим спо­со­бом мож­но из­ме­рять так­же темп-ру на­гре­тых тел в зем­ных ус­ло­ви­ях, что осо­бен­но важ­но для рас­ка­лён­ных ме­тал­лов и ке­ра­мик, где не­при­ме­ни­мы тра­диц. дат­чи­ки темп-ры. П. з. и. ис­поль­зу­ют для опи­са­ния по­то­ков лу­чи­стой энер­гии в эта­ло­нах яр­ко­сти из­лу­че­ния, не­об­хо­ди­мых для аб­со­лют­ной ка­либ­ров­ки при­ём­ни­ков све­та.