ПАРАМЕТРИ́ЧЕСКИЕ НЕУСТО́ЙЧИВОСТИ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ПАРАМЕТРИ́ЧЕСКИЕ НЕУСТО́ЙЧИВОСТИ, самопроизвольное нарастание возмущений колебательных систем и волновых структур, возникающее в результате пространственно-временнóй модуляции параметров, характеризующих частоту собств. колебаний. Простейшие примеры П. н.: раскачка механич. колебаний маятника переменной длины, раскачка электрич. колебаний резонансного контура с переменной ёмкостью или индуктивностью. Если параметр осциллятора меняется по гармонич. закону, то колебания описываются уравнением Матье:$$\frac{d^2x}{dt^2}+\omega^2_0[1+m\cos(\omega_нt)]x=0,\tag1$$ где $x$ – пространственная координата, $t$ – время, $ω_0$ – собств. частота осциллятора, $m$ – глубина модуляции, $ω_н$ – частота накачки.
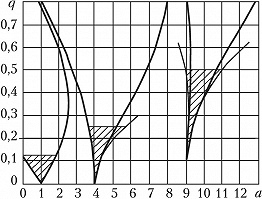
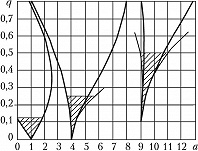
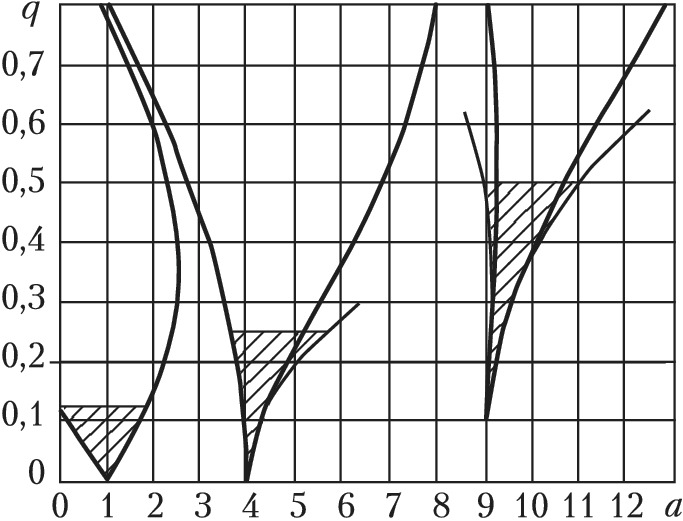
Уравнение (1) имеет решение $x=C_1x_M(ω_0t)e^{γt}+C_2x_M(–ω_0t)e^{–γt}$, где $γ$ – характеристич. показатель, $x_M(ω_0t)$ – ограниченная периодич. функция с периодом $π$ или $2π$, $C_1$ и $C_2$ – константы. Колебания раскачиваются, если $γ$ – действительная величина, и устойчивы, если $γ$ – мнимое число. На рис. 1 показана диаграмма П. н. (заштрихованные области) в координатах нормированной частоты $а=4ω_0^2/ω_н^2$ и индекса модуляции $q=mω_0^2/ω_н^2$. Колебания наименее устойчивы при параметрическом резонансе $a=1$, когда частота накачки в 2 раза превышает собств. частоту осциллятора: $ω_н=2ω_0$. Ширина резонанса и инкремент неустойчивости растут пропорционально глубине модуляции $m$. При наличии отстройки от резонансной частоты и поглощения П. н. проявляется, если $m$ превышает определённое пороговое значение; тогда возмущение начинает расти с уровня шумов (тепловых, квантовых и др.), отбирая энергию накачки. В нелинейном колебательном контуре модуляцию ёмкости можно осуществить, воздействуя мощным сигналом накачки на частоте $ω_н$ на включённый в цепь полупроводниковый диод.
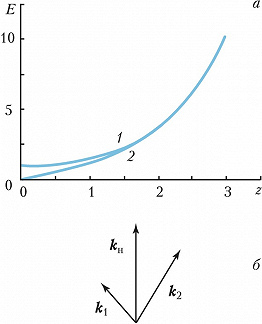
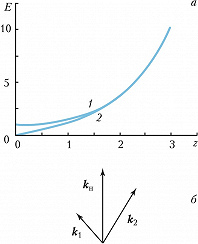
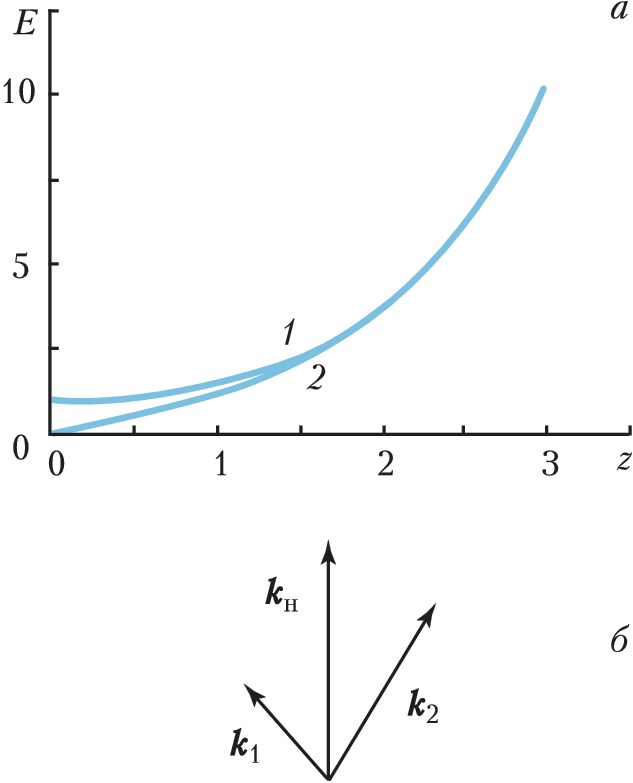
В нелинейных средах с распределёнными параметрами взаимодействуют волны и колебания разл. физич. природы. Напр., в плазме и диэлектриках интенсивная волна накачки осуществляет пространственно-временнýю модуляцию диэлектрич. или магнитной проницаемости по закону бегущей волны. Распространение слабых волн в среде с модулированным параметром описывается уравнением $$\frac{\partial^2 E}{\partial x^2}+\frac{\partial^2E}{\partial y^2}+\frac{\partial^2 E}{\partial z^2}+\frac{εμ}{c^2}\frac{\partial^2 [1+m\cos(ω_нt-k_нz)]E}{\partial t^2}=0,\tag2$$ где $E$ – напряжённость электрич. поля, $x$, $y$, $z$ – пространственные координаты, $ε$ – диэлектрич. проницаемость, $μ$ – магнитная проницаемость, $k_н$ – волновое число волны накачки. Решение уравнения (2) показывает, что в среде с квадратичной нелинейностью в поле волны накачки одновременно нарастают 2 волны (рис. 2, а) с частотами и волновыми векторами, удовлетворяющими условиям параметрич. резонанса (распадным условиям): $$ω_н=ω_1+ω_2,\quad \boldsymbol k_н=\boldsymbol k_1+\boldsymbol k_2.\tag3$$ Расположение волновых векторов при фазовом синхронизме (3) изображено на рис. 2, б. Для квазичастиц, обладающих энергией $\hbar ω$ и импульсом $\hbar \boldsymbol k$ ($\hbar$ – постоянная Планка), распадные условия можно интерпретировать как законы сохранения энергии и импульса при распаде кванта с энергией $\hbar ω_н$ и импульсом $\hbar \boldsymbol k_н$ на два других ($\hbar ω_1$, $\hbar \boldsymbol k_1$ и $\hbar ω_2$, $\hbar \boldsymbol k_2$). Т. к. при распаде энергия передаётся обоим образующимся квантам, они имеют меньшие частоты, чем квант волны накачки: $ω_1,ω_2<ω_н$. Если волна накачки и пробные волны (сигнальная и холостая) принадлежат одной и той же ветви дисперсионной кривой колебаний, то распадные условия выполняются не для всякой зависимости $ω(\boldsymbol k)$. Гораздо проще распадные условия выполняются, если в процесс П. н. вовлечены неск. ветвей колебаний. Это явление исследуется в физике плазмы, физике микроволн, нелинейной оптике и др.
П. н. волн лежат в основе вынужденных рассеяний. Сюда относится параметрическое рассеяние света, при котором происходит усиление квантовых и тепловых шумов и характерной особенностью которого является зависимость частоты рассеянного света от угла рассеяния (направления наблюдения). Это обусловлено тем, что при наклоне волновых векторов сигнальной и холостой волн появляется фазовая расстройка, которая компенсируется перестройкой частот $ω_1$ и $ω_2$. Т. о., углы, под которыми происходит рассеяние фотонов, зависят от дисперсионных свойств нелинейной среды – показателей преломления сигнальной и холостой волн. Рассеянный свет состоит из коррелированных попарно фотонов («бифотонов») и является «сжатым» (см. Сжатое состояние).
Другой пример – комбинационное рассеяние света, при котором роль холостой волны выполняют молекулярные колебания. Излучение, рассеянное с частотой, меньшей, чем у падающего света, называется стоксовым излучением, а излучение с большей частотой – антистоксовым.
При больших амплитудах накачки может возникнуть П. н. даже в отсутствие резонанса в случае, когда одна из волн, образующихся при распаде, не существует в среде в отсутствие накачки. Примером типичной нерезонансной П. н. является модуляционная неустойчивость. К П. н. относят и взрывную неустойчивость волн, возникающую в средах, где имеются волны с отрицательной энергией. Важную роль в параметрич. процессах в низкотемпературной плазме играет т. н. тепловая параметрич. неустойчивость.
П. н. может развиваться также в среде с кубич. нелинейностью при четырёхволновом взаимодействии в двух вариантах. В первом случае условие распадной неустойчивости выглядит как распад кванта накачки на 3 кванта: $$ω_н=ω_1+ω_2+ω_3,\quad \boldsymbol k_н=\boldsymbol k_1+\boldsymbol k_2+\boldsymbol k_3.$$ Во втором случае 2 кванта сливаются, а затем распадаются на 2 др. кванта: $$ω_н+ω_1=ω_2+ω_3,\quad \boldsymbol k_н+\boldsymbol k_1=\boldsymbol k_2+\boldsymbol k_3.\tag4$$
В вырожденном случае две частоты могут совпадать, и процесс становится трёхчастотным, как в среде с квадратичной нелинейностью, только с двухфотонной накачкой. Однако в среде с кубич. нелинейностью всегда присутствует самовоздействие: в соотношениях (4) все частоты и волновые векторы отвечают одной волне. Самовоздействие влияет на фазы волн и меняет характер параметрич. неустойчивости.