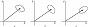СЖА́ТОЕ СОСТОЯ́НИЕ

СЖА́ТОЕ СОСТОЯ́НИЕ элек­тро­маг­нит­но­го по­ля, по­ле со спе­ци­фич. ха­рак­те­ри­сти­ка­ми, фор­ми­руе­мы­ми при его не­ли­ней­ном пре­об­ра­зо­ва­нии. По­ня­тие С. с. воз­ник­ло в 1960–70-х гг. при изу­че­нии ста­ти­стич. ха­рак­те­ри­стик из­лу­че­ния, де­таль­ном ис­сле­до­ва­нии не­обыч­ных свойств ла­зер­но­го из­лу­че­ния. Воз­мож­ны клас­сич. и кван­то­вые С. с. Клас­сич. С. с. яв­ля­ют­ся пе­рио­ди­че­ски не­ста­цио­нар­ны­ми слу­чай­ны­ми по­ля­ми с не­рав­ны­ми дис­пер­сия­ми квад­ра­тур­ных ком­по­нент (см. Кван­то­вая оп­ти­ка). Для кван­то­ван­ных по­лей в С. с. дис­пер­сия од­ной из ка­но­ни­че­ски со­пря­жён­ных ком­по­нент мень­ше дис­пер­сии в ко­ге­рент­ном со­стоя­нии.

Рис. 1. Изображение сжатых состояний электромагнитного поля на фазовой плоскости: а – произвольная ориентация эллипса сжатия (штриховая линия – область неопределённости когерентного состояния; вектор ...

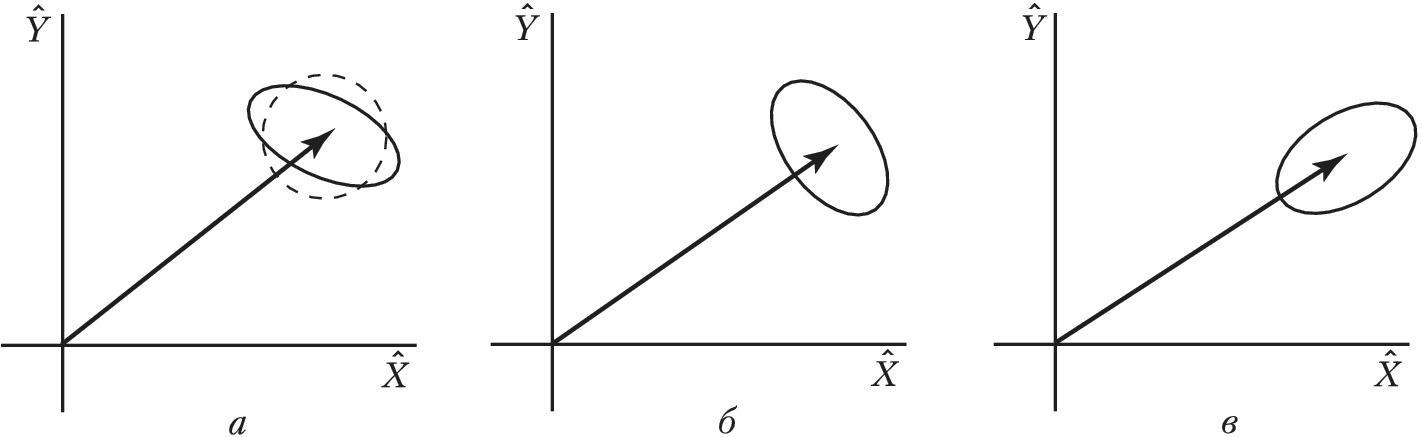
В кван­то­вой оп­ти­ке на­пря­жён­ность по­ля­ри­за­ци­он­ной ком­по­нен­ты од­но­мо­до­во­го элек­трич. по­ля опи­сы­ва­ет­ся опе­ра­то­ром $$\hat E = C[ \hat X \sin (ωt-kz) + \hat Y \cos(ωt-kz)],$$где $C=const$, $ω$ – час­то­та из­лу­че­ния, $k$ – вол­но­вое чис­ло, $z$ – на­прав­ле­ние рас­про­стра­не­ния из­лу­че­ния, $\hat X$ и $\hat Y$ – опе­ра­то­ры квад­ра­тур­ных ком­по­нент: $\hat X=(a^{+}+a)/2$, $\hat Y=i(a^{+}-a)/2$, $a(a^{+})$ – опе­ра­тор унич­то­же­ния (ро­ж­де­ния) фо­то­на. Опе­ра­то­ры квад­ра­тур удов­ле­тво­ря­ют ком­му­та­ци­он­но­му со­от­но­ше­нию $[\hat X,\hat Y] = \hat X \hat Y - \hat Y \hat X = i/2$, вслед­ст­вие че­го дис­пер­сии квад­ра­тур $σ_x^2$ и $σ_y^2$, рас­счи­тан­ные при усред­не­нии по со­стоя­нию по­ля, под­чи­ня­ют­ся со­от­но­ше­нию не­опре­де­лён­но­стей $σ_x^2σ_y^2 \geqslant 1/16$. В ко­ге­рент­ном и ва­ку­ум­ном со­стоя­ни­ях по­ля $σ_x^2=σ_y^2=1/4$. В кван­то­вом С. с. уро­вень од­ной из квад­ра­тур мень­ше $1/4$, а дру­гой – боль­ше $1/4$. При этом со­от­но­ше­ние не­опре­де­лён­но­стей не на­ру­ша­ет­ся. На фа­зо­вой плос­ко­сти квад­ра­тур­ных ком­по­нент С. с. со­от­вет­ст­ву­ет об­ласть не­оп­ре­де­лён­но­сти (дис­пер­сии) в ви­де эл­лип­са, ко­ге­рент­но­му со­стоя­нию – в ви­де кру­га (рис. 1, а).

Для ко­ге­рент­но­го со­стоя­ния по­ля ха­рак­тер­но пу­ас­со­нов­ское рас­пре­де­ле­ние фо­то­нов с дис­пер­си­ей $σ^2=\bar n$ ($\bar n$ – ср. чис­ло фо­то­нов). Для С. с. по­ля с по­дав­лен­ны­ми флук­туа­ция­ми чис­ла фо­то­нов $n$ и фа­зы $φ$ со­от­но­ше­ние не­оп­ре­де­лённо­стей име­ет вид $σ_n^2 σ_φ^2 ⩾ 1/4$. В за­ви­си­мо­сти от ори­ен­та­ции эл­лип­са сжа­тия при из­ме­ре­нии мо­жет быть по­дав­ле­ние флук­туа­ций числа фо­то­нов (рис. 1, б) или фа­зы (рис. 1, в). В пер­вом слу­чае диспер­сия $σ_n^2 < \bar n$, т. е. уро­вень флук­туа­ций фо­то­нов мень­ше, чем в ко­ге­рент­ном по­ле с пу­ас­со­нов­ской ста­ти­сти­кой фо­то­нов (т. н. суб­пу­ас­со­нов­ская ста­ти­сти­ка). При $σ_n^2=0$ флук­туа­ции фо­то­нов от­сут­ст­ву­ют (фо­ков­ское со­стоя­ние по­ля). При $σ_n^2 > \bar n$ го­во­рят о су­пер­пу­ас­со­нов­ской ста­ти­сти­ке фо­то­нов.

Рис. 2. Изображение когерентного (1) и поляризационно-сжатого (2) состояний на сфере Пуанкаре в стоксовом пространстве.

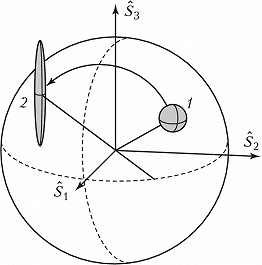
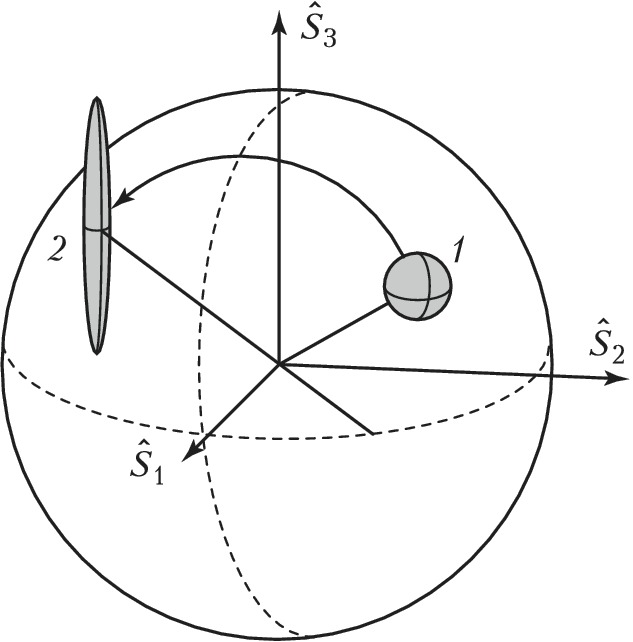
При кван­то­вом опи­са­нии по­ля­ри­за­ци­он­но­го со­стоя­ния по­ля ис­поль­зу­ют опе­ра­то­ры Сто­кса (их клас­сич. ана­ло­га­ми яв­ля­ют­ся па­ра­мет­ры Сто­кса): $$\hat S_0 = a_1^+ a_1 + a_2^+ a_2, \\ \hat S_1 = a_1^+ a_1 - a_2^+ a_2, \\ \hat S_2 = a_1^+ a_2 + a_2^+ a_1, \\ \hat S_3 = i(a_2^+ a_1 - a_1^+ a_2).$$ Здесь опе­ра­то­ры $a_1(a_1^+)$ и $a_2(a_2^+)$ от­но­сятся к ор­то­го­наль­ным по­ля­ри­за­ци­ям. Сто­ксо­вы опе­ра­то­ры под­чи­ня­ют­ся ком­му­та­ци­он­ным со­от­но­ше­ни­ям ал­геб­ры Ли груп­пы $SU(2)$. Ос­таль­ные ком­му­та­ци­он­ные со­от­но­ше­ния по­лу­ча­ют с по­мо­щью цик­лич. за­ме­ны ин­дек­сов. В ко­ге­рент­ном со­стоя­нии по­ля дис­пер­сии всех сто­ксо­вых па­ра­мет­ров оди­на­ко­вы $σ_j^2=〈S_0〉=\hat n_1 + \hat n_2 = \hat n_0$ $(j=0, 1, 2, 3)$, где $\hat n_0$ – ср. чис­ло фо­то­нов по­ля, не за­ви­ся­щее от ори­ен­та­ции по­ля­ри­за­ци­он­но­го ба­зи­са. По­ле, у ко­то­ро­го дис­пер­сия од­ной из сто­ксо­вых ком­по­нент мень­ше, чем в ко­ге­рент­ном со­стоя­нии, на­зы­ва­ют по­ля­ри­за­ци­он­но-сжа­тым. При этом об­ласть не­оп­ре­де­лён­но­сти сто­ксо­вых па­ра­мет­ров, имею­щая фор­му ша­ра, транс­фор­ми­ру­ет­ся, напр., в эл­лип­со­ид (рис. 2).

Осн. ме­то­да­ми по­лу­че­ния не­клас­сич. элек­тро­маг­нит­ных по­лей в С. с. яв­ля­ют­ся не­ли­ней­ные взаи­мо­дей­ст­вия: па­ра­мет­рич. про­цес­сы, са­мо­воз­дей­ст­вие, мно­го­фо­тон­ные про­цес­сы и т. п. Воз­мож­но так­же по­лу­че­ние С. с. в ла­зер­ных ис­точ­ни­ках из­лу­че­ния. Так, по­дав­лять фо­тон­ные флук­туа­ции в ла­зе­рах мож­но вве­де­ни­ем от­ри­ца­тель­ной об­рат­ной свя­зи ли­бо де­прес­си­ей флук­туа­ций на­кач­ки.

Элек­тро­маг­нит­ные по­ля в С. с. ис­поль­зу­ют для вы­со­ко­чув­ст­ви­тель­ных и вы­со­ко­точ­ных из­ме­ре­ний, для пе­ре­да­чи и об­ра­бот­ки кван­то­вой ин­фор­ма­ции (см. Кван­то­вая об­ра­бот­ка изо­бра­же­ний).