ПАРАМЕТРИ́ЧЕСКИЙ РЕЗОНА́НС
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
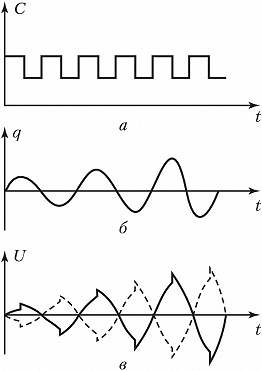
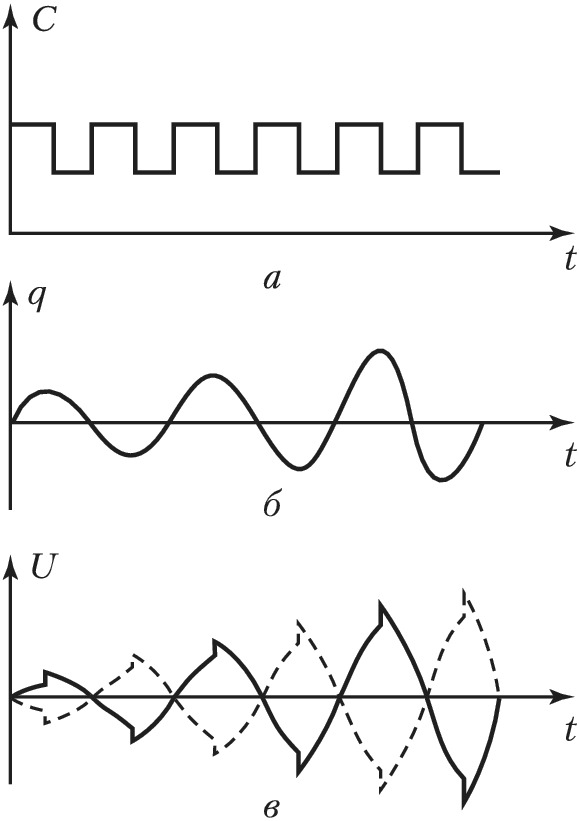
ПАРАМЕТРИ́ЧЕСКИЙ РЕЗОНА́НС, явление раскачки колебаний при периодич. изменении параметров тех элементов колебательной системы, в которых сосредоточена энергия колебаний (реактивные или энергоёмкие параметры). П. р. возможен в колебательных системах разл. физич. природы. Напр., в электрич. колебательном контуре реактивными параметрами являются ёмкость $C$ и индуктивность $L$, в которых запасены электрич. энергия $W_э=q^2/2C$ и магнитная энергия $W_м=LI^2/2$ (здесь $q$ – электрич. заряд на обкладках конденсатора, $I$ – ток в катушке индуктивности). Собств. колебания в контуре без потерь с постоянными $C$ и $L$ происходят с частотой $ω_0=1/\sqrt{LC}$. При этом полная энергия $W=W_э+W_м$, запасённая в контуре, остаётся неизменной; происходит лишь её периодич. трансформация из электрической в магнитную и обратно с частотой $2ω_0$. Изменение параметров $C$ и $L$, сопровождающееся работой внешних сил (накачка), приводит к изменению полной энергии системы. Если изменять, напр., ёмкость $C$ периодически в такт изменениям $W_э$ (обусловленным собств. колебаниями), уменьшая её в моменты, когда $q^2$ и $W_э$ максимальны, и увеличивая, когда эти величины равны нулю (рис. 1), то в среднем за период над системой совершается положительная работа и, следовательно, полная энергия и амплитуда колебаний будут монотонно нарастать.
П. р. наиболее эффективно проявляется при изменении параметров колебательной системы с периодом $T_н$, кратным полупериоду $T_0$ собств. колебаний системы:$$T_н≈nT_0/2,\quad ω_н=2ω_0/n,\qquad(1)$$ где $n$ – целое число, $ω_н=2π/T_н$ – частота накачки.
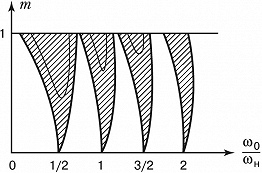
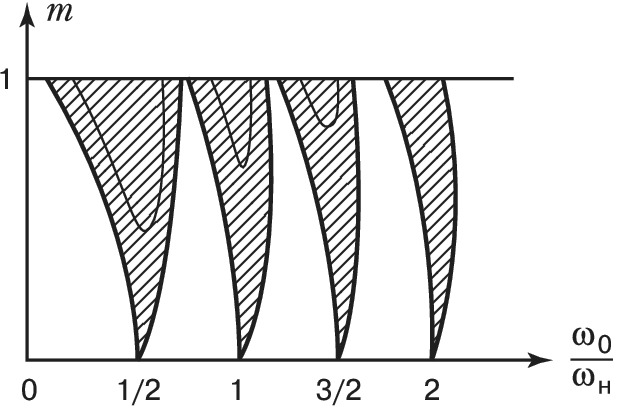
Нарастание колебаний возможно не только при точном выполнении соотношений (1), но и в некоторых конечных интервалах значений $ω_н$ вблизи $2ω_0/n$ (в т. н. зонах неустойчивости, рис. 2). Ширина зон тем больше, чем сильнее изменяются параметры $C$ и $L$. Изменение параметра, напр. ёмкости $C$, характеризуют величиной $$m=(C_{макс}-C_{мин})/(C_{макс}+C_{мин}),$$ называемой глубиной изменения параметра.
П. р. приводит к неустойчивости колебательной системы, т. е. к нарастанию малых начальных возмущений, напр. неизбежных во всякой системе флуктуаций, среди которых всегда найдётся составляющая с подходящей фазой по отношению к фазе изменения параметров. Если в системе имеются потери (напр., в контуре присутствует сопротивление $R$), то неустойчивость возникает только при достаточно больших изменениях $C$ или $L$, когда параметрич. накачка энергии превосходит потери. Зоны неустойчивости при этом соответственно уменьшаются или даже исчезают совсем (на рис. 2 эти зоны показаны тонкими линиями). Нарастание колебаний при П. р. не происходит беспредельно, а ограничивается при достаточно больших амплитудах разл. нелинейными эффектами. Напр., зависимость сопротивления от тока в контуре может приводить к увеличению потерь по мере возрастания амплитуды колебаний, а зависимость ёмкости от напряжения на ней – к изменению периода собств. колебаний $T_0$ и в результате к увеличению расстройки между значениями $ω_н$ и $2ω_0/n$. Равновесие наступает, когда параметрич. накачка энергии в среднем за период компенсируется потерями.
Пример механич. системы, в которой возможен П. р., – маятник в виде груза массы $M$, подвешенного на нити, длину $l$ которой можно изменять. Eсли уменьшать $l$ в нижнем и увеличивать в крайних положениях, то колебания могут раскачиваться. На П. р. основано самораскачивание на качелях, когда эффективная длина маятника периодически изменяется при приседаниях и вставаниях качающегося. П. р. учитывается в небесной механике при расчёте возмущений планетных орбит, вызванных влиянием др. планет.
В колебательных системах с несколькими степенями свободы (напр., в системе из двух связанных контуров или маятников) возможны собств. (нормальные) колебания (моды) с разл. частотами: $ω_1, ω_2,...$ Соответственно нарастание колебаний здесь возможно, напр., при изменении параметра с суммарной частотой: $ω_н=ω_1+ω_2$.
В системах с распределёнными параметрами (волновых системах), обладающих бесконечным числом степеней свободы, также возможно возбуждение нормальных колебаний в результате П. р. Классич. пример – опыт Мельде (1859), в котором наблюдалось возбуждение поперечных колебаний (стоячих волн) в струне, прикреплённой одним концом к ножке камертона, колебания которого периодически меняют натяжение струны с частотой, вдвое большей частоты собств. поперечных колебаний. Другой пример – опыт Фарадея (1831), в котором вертикальные колебания сосуда с водой приводят к возбуждению стоячей поверхностной волны с удвоенным периодом.
П. р. в волновых системах – это резонанс не только во времени, но и в пространстве. Напр., если накачка, изменяющая параметры среды, представляет собой бегущую волну с частотой $ω_н$ и волновым вектором $\boldsymbol k_н$, то возбуждение пары нормальных волн с частотами $ω_1$, $ω_2$ и волновыми векторами $\boldsymbol k_1$, $\boldsymbol k_2$ осуществляется, если выполняются условия: $$ω_н=ω_1+ω_2,\quad \boldsymbol k_н=\boldsymbol k_1+\boldsymbol k_2.\qquad(2)$$
На квантовом языке условия (2) означают, что при распаде кванта накачки на два др. кванта сохраняются как энергия $\hbar ω$, так и импульс $\hbar \boldsymbol k$ ($\hbar$ – постоянная Планка). Нарастание амплитуд волн во времени и в пространстве (распадная неустойчивость) также ограничивается нелинейными эффектами: если значит. часть энергии накачки израсходована на возбуждение волн, то возможен обратный процесс – рост энергии накачки за счёт ослабления волн на частотах $ω_1$, $ω_2$; в среде без потерь такой обмен энергией происходит периодически.
Параметрич. и нелинейные резонансные взаимодействия волн характерны, напр., для разл. типов волн в плазме, мощных световых волн (см. Параметрический генератор света), волн в электронных пучках и для др. волновых процессов.
-
Рис. 1. Связь между изменениями со временем t ёмкости С конденсатора (а), заряда q на его обкладках (б) и напряжения U (в) при параметрическом резонансе в колебательном контуре. -
Рис. 2. Области значений m, в которых возможен параметрический резонанс: ω0 – частота собственных колебаний; ωн – частота накачки (изменения параметра).
