ЛАНДА́У ТЕО́РИЯ СВЕРХТЕКУ́ЧЕСТИ

Спектр элементарных возбуждений в HeII, полученный в нейтронных экспериментах; ℰ – энергия квазичастицы, p – её импульс.

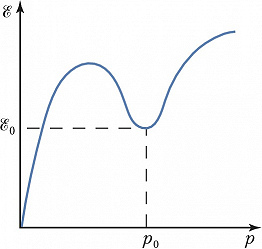
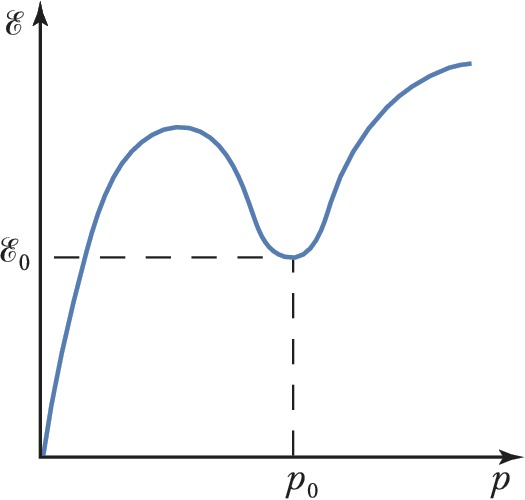
ЛАНДА́У ТЕО́РИЯ СВЕРХТЕКУ́ЧЕСТИ, объ­яс­ня­ет сверх­те­ку­чие свой­ст­ва кван­то­вой жид­ко­сти Не II при тем­пе­ра­ту­рах ни­же темп-ры т. н. $λ$-пе­ре­хо­да ($T_λ=2,17$К при дав­ле­нии на­сы­щен­ных па­ров ге­лия) (см. Сверх­те­ку­честь). Пред­ло­же­на Л. Д. Лан­дау в 1941 и по­лу­чи­ла назв. двух­жид­ко­ст­ной гид­ро­ди­на­ми­ки. Л. т. с. свя­зы­ва­ет сверх­те­ку­честь Не II (см. Ге­лий жид­кий) со свой­ст­ва­ми спек­тра его эле­мен­тар­ных воз­бу­ж­де­ний – ква­зи­ча­стиц. При $T=0$ К жид­кий ⁴Не на­хо­дит­ся в ос­новном со­стоя­нии. При температуpax, близ­ких к аб­со­лют­но­му ну­лю, жид­кость пе­ре­хо­дит в од­но из воз­бу­ж­дён­ных со­стоя­ний, ко­то­рые мож­но пред­ста­вить как со­во­куп­ность ква­зи­ча­стиц. Про­стей­ши­ми ква­зи­ча­сти­ца­ми в жид­ко­сти яв­ля­ют­ся ко­ле­бания её плот­но­сти – фо­но­ны. За­кон дис­пер­сии фо­но­нов, т. е. за­ви­си­мость их энер­гии $ℰ$ от им­пуль­са $p$, име­ет вид $ℰ=cp$, где $c$ – ско­рость зву­ка. Для объ­яс­не­ния тем­пе­ра­тур­но­го хо­да тер­мо­ди­на­мич. па­ра­мет­ров Не II Лан­дау по­сту­ли­ро­вал, что спектр эле­мен­тар­ных воз­бу­ж­де­ний Не II, кро­ме фо­нон­но­го уча­ст­ка, со­дер­жит уча­сток с за­ко­ном дис­пер­сии $ℰ=ℰ_0+(\boldsymbol p-\boldsymbol p_0)2/2m_{рт}$, и на­звал со­от­вет­ст­вую­щие ква­зи­ча­сти­цы ро­то­на­ми ($m_{рт}$ – эф­фек­тив­ная мас­са ро­то­на). Фор­ма спек­тра, пред­ло­жен­ная Лан­дау, впо­след­ст­вии бы­ла под­твер­жде­на в экс­пе­ри­мен­тах по не­уп­ру­го­му рас­сея­нию ней­тро­нов на Не II (рис.).

Кван­то­вая жид­кость с рас­смот­рен­ным Лан­дау спек­тром воз­бу­ж­де­ний при те­че­нии по тру­бе те­ря­ет им­пульс толь­ко за счёт воз­бу­ж­де­ний, воз­ни­каю­щих при ско­ро­стях те­че­ния $v>v_{кр}= \min[ℰ (p)/p]$. Т. о., кван­то­вые жид­ко­сти, спектр ко­то­рых удов­ле­тво­ря­ет ус­ло­вию $\min[ℰ (p)/p]≠ 0$, об­ла­да­ют сверх­те­ку­че­стью (кри­те­рий сверх­те­ку­че­сти Лан­дау). Спектр НеII удов­ле­тво­ря­ет это­му кри­те­рию при ско­ро­стях те­че­ния $v\lt v_{кр} \approx \mathscr E_0/p_0$. Од­на­ко зна­че­ние на­блю­дае­мой кри­тич. ско­ро­сти $v_{кр}$ при­мер­но на два по­ряд­ка ни­же ука­зан­ной ве­ли­чи­ны, что свя­за­но с рож­де­ни­ем в жид­ко­сти кван­то­ван­ных вих­рей – вих­ре­вых ли­ний, на ко­то­рых на­ру­ше­на сверх­те­ку­честь.

При $Т≠0$ К НеII со­сто­ит из двух ком­по­нент: нор­маль­ной и сверх­те­ку­чей. Со­глас­но Лан­дау, сверх­те­ку­чая ком­по­нен­та – иде­аль­ная жид­кость с по­тен­ци­аль­ным те­че­ни­ем – не об­ла­да­ет эн­тро­пи­ей $S$ и не ис­пы­ты­ва­ет со­про­тив­ле­ния при про­те­ка­нии сквозь уз­кие ка­пил­ля­ры. Её плот­ность $ρ_s$ при $T=0$ К сов­па­да­ет с пол­ной плот­но­стью жид­ко­сти $ρ$ и с рос­том $T$ умень­ша­ет­ся до ну­ля при $T=Т_λ$. Нор­маль­ная ком­по­нен­та – ос­таль­ная часть жид­ко­сти с плот­но­стью $ρ_n=ρ-ρ_s$ – ве­дёт се­бя как обыч­ная вяз­кая жид­кость. При темп-pax, близ­ких к аб­со­лют­но­му ну­лю, нор­маль­ная ком­по­нен­та пред­став­ля­ет со­бой газ воз­бу­ж­де­ний в иде­аль­ной жид­ко­сти (газ фо­но­нов и ро­то­нов). Ано­маль­но вы­со­кая те­п­ло­про­вод­ность НеII свя­за­на с тем, что те­п­ло­та в нём мо­жет пе­ре­но­сить­ся дви­же­ни­ем нор­маль­ной ком­по­нен­ты при от­сут­ст­вии пол­но­го по­то­ка мас­сы, ко­то­рый ком­пен­си­ру­ет­ся про­ти­во­то­ком сверх­те­ку­чей ком­по­нен­ты, не не­су­щей те­п­ло­ты. Бла­го­да­ря та­ко­му ме­ха­низ­му пе­ре­но­са те­п­ло­ты в НеII, кро­ме обыч­но­го (пер­во­го) зву­ка (волн плот­но­сти), су­ще­ст­ву­ет вто­рой звук – тем­пе­ра­тур­ные вол­ны.

Двух­жид­ко­ст­ная гид­ро­ди­на­ми­ка Лан­дау, кро­ме урав­не­ний, со­дер­жа­щих обыч­ные гид­ро­ди­на­мич. пе­ре­мен­ные (ρ , плот­ность по­то­ка час­тиц $j, S$), вклю­ча­ет в се­бя урав­не­ние для ско­ро­сти сверх­те­ку­чей ком­по­нен­ты: $$𝜕v_s/𝜕t=–∇μ,$$ где $μ$ – хи­мич. по­тен­ци­ал, $t$ – вре­мя. Это урав­не­ние оп­ре­де­ля­ет осн. свой­ст­во сверх­те­ку­че­го 4Не: для под­дер­жа­ния ста­цио­нар­но­го те­че­ния сверх­те­ку­чей ком­по­нен­ты не тре­бу­ет­ся раз­но­сти хи­мич. по­тен­циа­лов на кон­цах ка­на­ла, т. е. сверх­те­ку­чее дви­же­ние про­ис­хо­дит без пе­ре­па­да дав­ле­ния. Ина­че го­во­ря, вяз­кость сверх­те­ку­чей ком­по­нен­ты рав­на ну­лю. На­ли­чие раз­но­сти хи­мич. по­тен­циа­лов $(∇μ≠0)$ при­во­дит к ус­ко­ре­нию сверх­те­ку­чей ком­по­нен­ты. Двух­жид­ко­ст­ная мо­дель объ­яс­ня­ет боль­шин­ст­во эф­фек­тов, при­су­щих сверх­те­ку­чей жид­ко­сти: ме­ха­но­ка­ло­ри­че­ский эф­фект; тер­мо­ме­ха­ни­че­ский эф­фект; су­ще­ст­во­ва­ние кри­тич. ско­ро­сти те­че­ния, на­чи­ная с ко­то­рой сверх­те­ку­чая ком­по­нен­та ис­пы­ты­ва­ет тре­ние; су­ще­ст­во­ва­ние плён­ки на стен­ках со­су­да, бла­го­да­ря ко­то­рой вы­рав­ни­ва­ют­ся уров­ни НеII в со­су­дах, раз­де­лён­ных стен­кой; тре­тий звук, чет­вёр­тый звук и др. (см. Звук в сверх­те­ку­чем ге­лии).

Урав­не­ния двух­жид­ко­ст­ной гид­ро­ди­на­ми­ки Лан­дау, по­лу­чен­ные для НеII, по­слу­жи­ли ос­но­вой для по­строе­ния гид­ро­ди­на­ми­ки др. сверх­те­ку­чих жид­ко­стей (сме­сей ³Не-⁴Не, фаз ³Не) и жид­ких кри­стал­лов.

По совр. пред­став­ле­ни­ям, кри­те­рий Лан­дау не яв­ля­ет­ся оп­ре­де­ляю­щим для ре­ше­ния во­про­са о сверх­те­ку­че­сти кван­то­вой жид­ко­сти. Име­ют­ся при­ме­ры сверх­те­ку­чих сис­тем, где кри­те­рий Лан­дау за­ве­до­мо на­ру­шен (бес­ще­ле­вые сверх­про­вод­ни­ки, сверх­те­ку­чая А-фа­за ³Не).