ГА́ММА-ЛА́ЗЕР

ГА́ММА-ЛА́ЗЕР, ис­точ­ник ко­ге­рент­но­го элек­тро­маг­нит­но­го из­лу­че­ния $γ$-диа­па­зо­на. Час­то ис­поль­зу­ют­ся со­кра­ще­ния «гра­зер» или «га­зер», от англ. фра­зы «Gamma Ray Amplification by Stimulated Emission of Radiation» («уси­ле­ние $γ$-из­лу­че­ния с по­мо­щью вы­ну­ж­ден­но­го из­лу­че­ния»). По­ка ге­не­ра­ция вы­ну­ж­ден­но­го из­лу­че­ния в $γ$-диа­па­зо­не не осу­ще­ст­в­ле­на. По­лу­че­ние ге­не­ра­ции в рент­ге­нов­ском и $γ$-диа­па­зо­нах от­кры­ло бы но­вые пер­спек­ти­вы в рент­ге­нов­ском струк­тур­ном ана­ли­зе

, ли­то­гра­фии, ядер­ной фи­зи­ке (воз­дей­ст­вие на те­че­ние ядер­ных ре­ак­ций) и др.

Идея Г.-л. воз­ник­ла в свя­зи с по­яв­ле­ни­ем оп­тич. ла­зе­ра

и от­кры­ти­ем Мёсс­бау­эра эф­фек­та

 >>

. От­кры­тие ис­пус­ка­ния $γ$-кван­тов без от­да­чи по­ста­ви­ло во­прос о реа­ли­за­ции вы­ну­ж­ден­но­го из­лу­че­ния сис­те­мой воз­бу­ж­дён­ных ядер. Впер­вые на эту воз­мож­ность ука­зал рос. фи­зик Л. А. Рив­лин в 1961. В 1961–65 од­но­вре­мен­но и не­за­ви­си­мо не­сколь­ко сов. и амер. групп фи­зи­ков за­ни­ма­лись раз­ра­бот­кой схем Г.-л. на эф­фек­те Мёс­сбау­эра. Для соз­да­ния ак­тив­ной сре­ды пред­по­ла­га­лось ис­поль­зо­вать ра­дио­хи­мич. ме­то­ды вы­де­ле­ния дол­го­жи­ву­щих ядер­ных изо­ме­ров с по­сле­дую­щим вве­де­ни­ем их в крис­тал­лич. мат­ри­цу или вы­ра­щи­ва­ни­ем из этих ядер ак­тив­ных крис­тал­лов.

Для воз­ник­но­ве­ния на­рас­таю­щей ла­ви­ны ко­ге­рент­ных $γ$-кван­тов не­об­хо­ди­мо: 1) соз­дать ин­вер­сию на­се­лён­но­стей

ра­бо­чих уров­ней; 2) ве­ро­ят­ность вы­нуж­ден­но­го из­лу­че­ния долж­на быть вы­ше ве­ро­ят­но­сти по­гло­ще­ния или рас­сея­ния $γ$-кван­тов в ак­тив­ной сре­де ла­зе­ра. Т. о., воз­ник­шее в сре­де $γ$-из­лу­че­ние (в ре­зуль­та­те спон­тан­но­го рас­па­да отд. ядер) бу­дет уси­ли­вать­ся, ес­ли плот­ность $N$ воз­бу­ж­дён­ных ядер пре­вы­ша­ет по­ро­го­вое зна­че­ние $N^*$, ко­то­рое оп­ре­де­ля­ет­ся из ус­ло­вия ра­вен­ст­ва ко­эф. $μ$ ре­зо­нанс­но­го вы­ну­ж­ден­но­го из­лу­че­ния (ко­эф. кван­то­во­го уси­ле­ния) и ко­эф. $δ$ не­ре­зо­нанс­ных по­терь энер­гии: $μ=δ$. Ко­эф. уси­ле­ния $μ$ оп­ре­де­ля­ет­ся фор­му­лой: $$\mu=\frac{\lambda^2}{2\pi} \frac{\hbar}{Γ \tau} \frac{\beta}{1+\alpha}N.\qquad (1)$$ Здесь $λ$ – дли­на вол­ны $γ$-из­лу­че­ния, $ℏ$ – по­сто­ян­ная План­ка, $Γ$ – спек­траль­ная ши­ри­на ре­зо­нанс­но­го пе­ре­хо­да яд­ра в кри­стал­ле, $τ$ – вре­мя жиз­ни яд­ра в изо­мер­ном со­стоя­нии, $α$ – ко­эф. кон­вер­сии внут­рен­ней

 >>

, $β$ – т. н. ко­эф. ветв­ле­ния, учи­ты­ваю­щий воз­мож­ность пе­ре­хо­да яд­ра на др. уров­ни, ле­жа­щие вы­ше ниж­не­го ра­бо­че­го, ес­ли ге­не­ра­ция идёт с бо­лее вы­со­ких уров­ней, чем пер­вый воз­бу­ж­дён­ный ($β=1$ для ге­не­ра­ции с пер­во­го воз­бу­ж­дён­но­го уров­ня яд­ра). Не­ре­зо­нан­с­ные по­те­ри в об­лас­ти энер­гий $γ$-кван­тов, в ко­то­рой ве­ро­ят­ность эф­фек­та Мёс­с­бау­эра ве­ли­ка, оп­ре­де­ля­ют­ся в осн. фо­то­эф­фек­том

 >>

. Для кри­стал­лич. мат­риц с $δ≈ 10 см^{–1}$, по­ла­гая в $(1) λ= 1 Å , α≈β≈ 1$, по­лу­чим $$N^*=1,3 \cdot10^{17} Γ \tau.\qquad (2)$$

Ес­ли ши­ри­на ли­нии $γ$-пе­ре­хо­да рав­на ес­те­ст­вен­ной, $Γτ=1$, то кри­тич. плот­ность воз­бу­ж­дён­ных изо­мер­ных ядер со­став­ля­ет не­зна­чит. часть плот­но­сти ато­мов в твёр­дом те­ле (по­ряд­ка 10²³ ато­мов/см³). Не мёс­сбау­эров­ский ва­ри­ант Г.-л. прак­ти­че­ски не­воз­мо­жен, по­сколь­ку для ядер с атом­ны­ми но­ме­ра­ми $Z$ из се­ре­ди­ны пе­рио­ди­че­ской сис­те­мы эле­мен­тов до­п­ле­ров­ское уши­ре­ние ли­нии $ΓD≈10^{13}$ Гц и уже при $τ=10^{–7}$ с по­ро­го­вая плот­ность изо­мер­ных ядер (2) вы­хо­дит за пре­де­лы плот­но­сти твёр­до­го те­ла.

Об­су­ж­да­ет­ся воз­мож­ность ис­поль­зо­ва­ния бо­зе-эйн­штей­нов­ско­го кон­ден­са­та в ка­че­ст­ве ра­бо­чей сре­ды Г.-л. Это, с од­ной сто­ро­ны, обес­пе­чи­ва­ет ма­лую ши­ри­ну ли­нии $γ$-пе­ре­хо­да, а с дру­гой – да­ёт воз­мож­ность раз­ви­тия схем со скры­той ин­вер­си­ей на­се­лён­но­стей.

Ве­ро­ят­ность эф­фек­та Мёс­сбау­эра близ­ка к 1 толь­ко при зна­че­ни­ях энер­гии пе­ре­хо­да $ℏω<150$ кэВ. Для кван­тов боль­шей энер­гии ве­ро­ят­ность из­лу­че­ния без от­да­чи рез­ко па­да­ет. Это ог­ра­ни­чи­ва­ет верх­нее зна­че­ние ве­ли­чи­ны энер­гии γ-кван­тов, дос­ти­жи­мое в Г.-л. на ядер­ных пе­ре­хо­дах. Ниж­нее зна­че­ние энер­гии ра­диац. пе­ре­хо­дов ядер, при­год­ных для ге­не­ра­ции γ-из­лу­че­ния, оп­ре­де­ля­ется бы­ст­рым рос­том се­че­ния фо­то­эф­фек­та с умень­ше­ни­ем энер­гии γ -кван­тов. По­это­му об­ласть при­год­ных энер­гий ра­диац. пе­ре­хо­дов ядер оп­ре­де­ля­ет­ся не­ра­вен­ст­ва­ми: $10\ кэВ<ℏω<150 \ кэВ$.

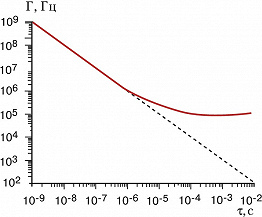
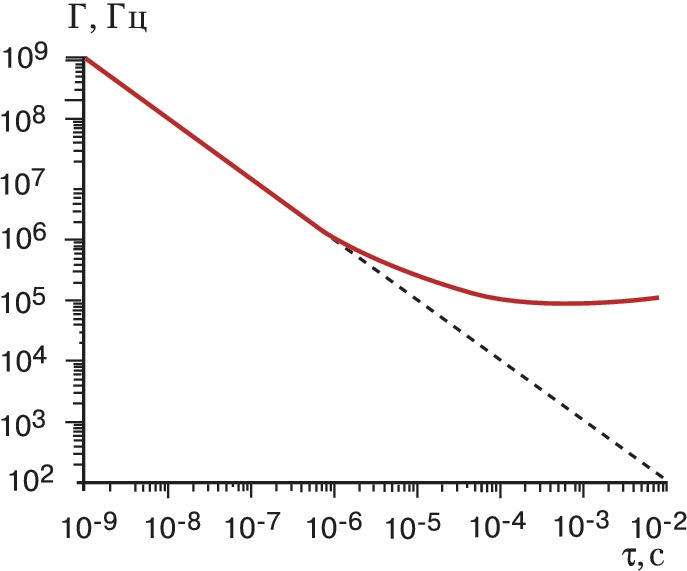
Мо­де­ли Г.-л. на ядер­ных пе­ре­хо­дах мож­но раз­де­лить на две груп­пы: Г.-л. на ко­рот­ко­жи­ву­щих ($τ⩽10^{–5}$ с) и дол­го­жи­ву­щих ($τ≫10^{–5}$ с) изо­ме­рах. Гра­нич­ное зна­че­ние $τ=10^{–5}$ с обу­слов­ле­но тем, что при $τ⩽10^{–5}$ с ши­ри­на мёс­сбау­эров­ской ли­нии $γ$-пе­ре­хо­да близ­ка к ес­те­ст­вен­ной ши­ри­не $Γτ≈1$. При $τ≫10^{–5}$ с ши­ри­на ли­нии не за­ви­сит от вре­ме­ни жиз­ни и рав­на при­бли­зи­тель­но $10^5$ Гц, а сле­до­ва­тель­но, $Γτ≫1$ (рис.). Это и оп­ре­де­ли­ло осн. труд­но­сти пер­вых мо­де­лей Г.-л. на дол­го­жи­ву­щих изо­ме­рах.

Не­из­беж­ные на­ру­ше­ния иде­аль­но­сти кри­стал­лич. ре­шёт­ки, хи­мич. и квад­ру­поль­ные сдви­ги ре­шёт­ки, а так­же маг­нит­ное ди­поль-ди­поль­ное взаи­мо­дей­ст­вие ядер при­во­дят к уши­ре­нию ли­нии $γ$-ре­зо­нан­са.

Про­гресс в раз­ра­бот­ке схем Г.-л. на дол­го­жи­ву­щих изо­ме­рах был дос­тиг­нут бла­го­да­ря ра­бо­там Р. В. Хох­ло­ва

с со­труд­ни­ка­ми, ко­то­рые пред­ло­жи­ли при­ме­нить ме­то­ды ЯМР-спек­тро­ско­пии твёр­дых тел (см. Ядер­ный маг­нит­ный ре­зо­нанс

 >>

) для су­же­ния ли­нии $γ$-ре­зо­нан­са. Спе­ци­аль­но по­доб­ран­ная по­сле­до­ва­тель­ность им­пуль­сов с час­то­той, со­от­вет­ст­вую­щей пе­ре­хо­дам ме­ж­ду маг­нит­ны­ми по­ду­ров­ня­ми ра­бо­чих уров­ней ядер, по­зво­ля­ет по­да­вить эти ме­ха­низ­мы уши­ре­ния ли­нии. Бы­ст­рая пе­ре­ори­ен­та­ция ядер ра­дио­час­тот­ным по­лем ос­лаб­ля­ет ди­поль-ди­поль­ное взаи­мо­дей­ст­вие, ус­ред­няя его ве­ли­чи­ну, имею­щую раз­ный знак при разл. ори­ен­та­ции спи­нов. Од­но­вре­мен­но ос­лаб­ля­ет­ся маг­нит­ное взаи­мо­дей­ст­вие ядер с со­сед­ни­ми ато­ма­ми и взаи­мо­дей­ст­вие элек­трич. квад­ру­поль­ных мо­мен­тов ядер с внут­ри­кри­стал­лич. элек­трич. по­ля­ми. Ана­ло­гич­но по­дав­ля­ет­ся т. н. хи­мич. сдвиг. Т. о., ис­кусств. су­же­ние ли­нии $γ$-ре­зо­нан­са по­зво­ля­ет при­бли­зить­ся к соз­да­нию Г.-л. на дол­го­жи­ву­щих изо­ме­рах.

В схе­мах на ко­рот­ко­жи­ву­щих изо­ме­рах (В. И. Голь­дан­ский

, Ю. М. Ка­ган

 >>

) осн. про­бле­ма – ме­ха­низм воз­бу­ж­де­ния (на­кач­ка) ядер. На­кач­ка долж­на быть ин­тен­сив­ной и се­лек­тив­ной. Эф­фек­тив­но воз­бу­ж­дая ра­бо­чие яд­ра, она долж­на ми­ни­маль­но воз­му­щать со­стоя­ние ре­шёт­ки кри­стал­ла. Наи­бо­лее близ­ки к вы­пол­не­нию этих тре­бо­ва­ний сле­дую­щие ви­ды воз­бу­ж­де­ния ядер: за­хват те­п­ло­вых ней­тро­нов (см. Ра­диа­ци­он­ный за­хват

 >>

), воз­бу­ж­де­ние из­лу­че­ни­ем (син­хро­трон­ным, ха­рак­те­ри­сти­че­ским, рент­ге­нов­ским и др.), а так­же воз­бу­ж­де­ние пуч­ком за­ря­жен­ных час­тиц.

Ис­сле­до­ва­лась так­же воз­мож­ность со­вме­ще­ния пре­иму­ществ двух схем: не­кри­тич­но­сти па­ра­мет­ров на­кач­ки в схе­ме на дол­го­жи­ву­щих изо­ме­рах и ма­ло­сти про­из­ве­де­ния $Γτ$ в схе­ме на ко­рот­ко­живу­щих изо­ме­рах. Это мож­но, напр., осу­ще­ст­вить при на­ли­чии двух близ­ко рас­по­ло­жен­ных ядер­ных уров­ней с разл. вре­ме­на­ми жиз­ни и раз­ни­цей энер­гий, со­от­вет­ст­вую­щей энер­гии кван­та оп­тич. или УФ-ла­зе­ра, ко­то­рый мо­жет сти­му­ли­ро­вать пе­ре­ход с дол­го­жи­ву­ще­го ядер­но­го по­ду­ров­ня на ко­рот­ко­жи­ву­щий. Т. о., на­кач­ка осу­ще­ст­в­ля­ет­ся на дол­го­жи­ву­щем пе­ре­хо­де, а ге­не­ра­ция – на ко­рот­ко­жи­ву­щем. Та­кие схе­мы на­зы­ва­ют­ся триг­гер­ны­ми.

Из-за низ­кой от­ра­жа­тель­ной спо­соб­но­сти ма­те­риа­лов в $γ$-диа­па­зо­не тра­диц. схе­ма оп­тич. ре­зо­на­то­ров не­при­год­на. Од­на­ко воз­мож­но ис­поль­зо­ва­ние ано­маль­но низ­ко­го по­гло­ще­ния $γ$-из­лу­че­ния по оп­ре­де­лён­ным на­прав­ле­ни­ям в кри­стал­ле, для ко­то­рых вы­пол­ня­ет­ся Брэг­га – Вуль­фа ус­ло­вие

(эф­фект Бор­ма­на). В этих на­прав­ле­ни­ях про­ис­хо­дит силь­ное от­ра­же­ние от атом­ных плос­ко­стей кри­стал­ла, в нём рас­про­стра­ня­ют­ся две пло­ские вол­ны под уг­лом друг к дру­гу, и на­пря­жён­ность ин­тер­фе­рен­ци­он­но­го элек­трич. по­ля в уз­лах ре­шёт­ки рав­на 0. По­это­му γ-кван­ты не те­ря­ют энер­гию на вы­ры­ва­ние элек­тро­нов и рез­ко по­ни­жа­ет­ся ве­ро­ят­ность по­гло­ще­ния $γ$-кван­тов. Соз­да­ние мно­го­слой­ных на­но­ст­рук­тур по­зво­ля­ет на­де­ять­ся на по­лу­че­ние от­ра­жаю­щих зер­кал для γ-диа­па­зо­на.

Ге­не­ра­ция ко­ге­рент­но­го $γ$-из­лу­че­ния воз­мож­на так­же при вы­ну­ж­ден­ной ан­ни­ги­ля­ции элек­трон­но-по­зи­трон­ных пар, при взаи­мо­дей­ст­вии вы­со­ко­энер­ге­тич. встреч­ных пуч­ков за­ря­жен­ных час­тиц с про­стран­ст­вен­но-пе­рио­ди­че­ски­ми струк­ту­ра­ми. Ме­ха­низ­мом ге­не­ра­ции ко­ге­рент­но­го $γ$-из­лу­че­ния мо­жет быть так­же т. н. сверх­из­лу­че­ние, ко­гда ко­ге­рент­ность ис­пу­щен­ных фо­то­нов яв­ля­ет­ся след­ст­ви­ем кор­ре­ля­ции со­стоя­ний от­дель­ных ядер-из­лу­ча­те­лей.