МОДУЛЯ́ЦИЯ КОЛЕБА́НИЙ И ВОЛН
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
МОДУЛЯ́ЦИЯ КОЛЕБА́НИЙ И ВОЛН, изменение во времени параметров колебаний и волн. Существует неск. видов модуляции: амплитудная (АМ), частотная (ЧМ) и фазовая (ФМ), когда медленно меняется соответственно амплитуда, частота и фаза колебаний. Для оптич. волн используется также поляризационная модуляция, когда меняется поляризация излучения.
Модуляцию сигнала $f(t)$ можно представить в виде $$f(t)=A(t) \cos [ω_0t+φ(t)], \qquad(1)$$ где $t$ – время, $ω_0$ – постоянная «несущая» частота, на которую накладывается низкочастотный модулирующий сигнал, $A$ – амплитуда, $φ$ – фаза колебаний, которые, как и частота $ω=ω_0+dφ/dt$, могут медленно (в масштабе периода несущей частоты $T=2π/ω_0$) изменяться во времени. В спектральном представлении выражение (1) определяет колебание с узким по сравнению с несущей частотой частотным спектром. В более общем случае модулированное колебание можно представить в виде $f(t)=A(t) \cos θ(t)$, где $θ$ – полная фаза, так что частота $ω (t)=dθ /dt$ может меняться медленно, но сколь угодно сильно; при этом спектр колебаний может быть широким. Модулирующие сигналы могут иметь сложную форму, напр. состоять из закодированных последовательностей импульсов (см. Импульсная модуляция).
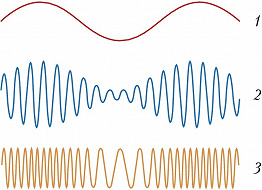
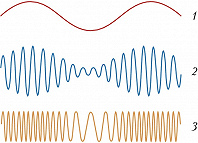
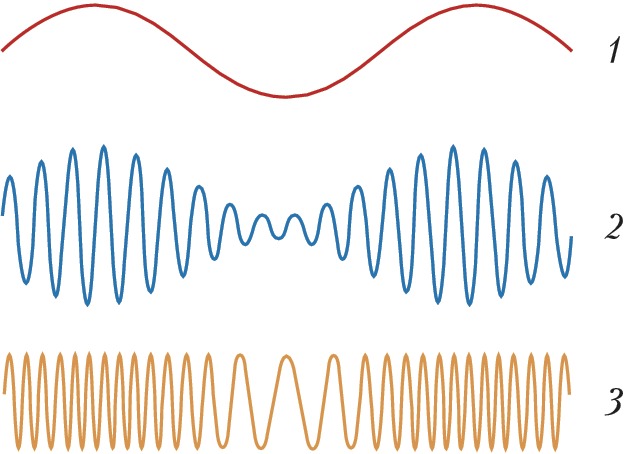
Способы М. к. и в. и модулирующие устройства – модуляторы – столь же разнообразны, как и устройства, в которых они применяются. Напр., в генераторе радиопередатчика управляющий сигнал модулирует на звуковых частотах амплитуду или частоту несущего колебания (рис. 1), которое излучается антенной как радиоволна. B приёмнике высокочастотное несущее колебание удаляется посредством детектирования, a модулирующий звуковой сигнал подаётся на громкоговоритель. В телевидении используются сложные широкополосные сигналы совместно с оптич. преобразователями. Для модуляции света в лазерах часто используют эффекты, приводящие к изменению показателя преломления материала под действием внешнего поля, напр. эффект Керра.
Для модулированных волн, амплитуда и фаза которых меняются не только во времени, но и в пространстве, вместо формулы (1) имеем:$$f(t, \boldsymbol {r})=A(t,\boldsymbol {r}) \cos [ω_0t-\boldsymbol {k}_0\boldsymbol {r}+φ(t,\boldsymbol {r})] \; \text {или} \; f(t,\boldsymbol {r})=A(t,\boldsymbol {r}) \cos θ(t,\boldsymbol {r}), \qquad (2)$$ где $\boldsymbol {r} $ – радиус-вектор точки в пространстве. Такая волна имеет как временной $T$, так и пространственный период $Λ=2π /|\boldsymbol {k}|$, где $\boldsymbol {k}$ – волновой вектор.
Модуляция волны может быть вызвана разл. причинами, напр. вариациями начальных условий во времени, граничных условий в пространстве или медленными изменениями параметров среды во времени и пространстве.
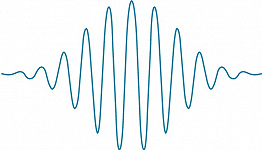
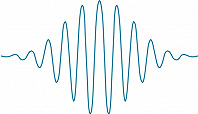
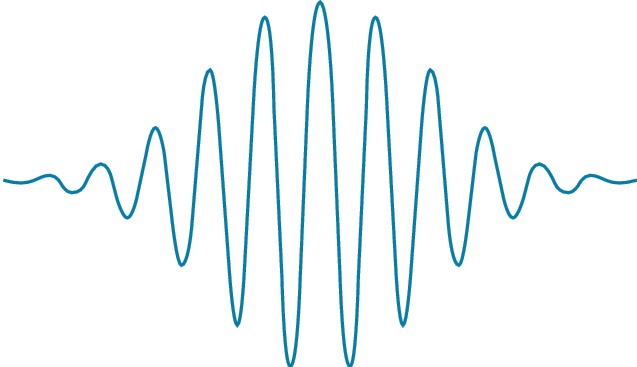
Типичный пример модулированной волны – волновой пакет (рис. 2), распространяющийся с групповой скоростью $c_r=dω /dk$; она может отличаться от фазовой скорости $c_{\text ф}=ω_0/k_0$, с которой перемещаются максимумы и минимумы пространственных осцилляций. Зависимость $ω(k)$, называемая дисперсией волн, определяется свойствами среды. Групповая и фазовая скорости равны только в недиспергирующих средах; напр., радиоволны и звук распространяются в воздухе почти без дисперсии, а волны на поверхности глубокой жидкости сильно диспергируют: их групповая скорость вдвое меньше фазовой. Если волновой пакет распространяется в диспергирующей среде достаточно долго, он постепенно расплывается, в итоге превращаясь в частотно-модулированную волну, в которой каждая группа (цуг) движется со своей групповой скоростью, определяемой соответствующей локальной частотой.
В нелинейных средах с дисперсией эволюция волны определяется «конкуренцией» между дисперсией, которая обычно приводит к расплыванию пакета, и нелинейностью, способной обострять волновой фронт. Эволюция таких волн может развиваться по разл. сценариям. Один из них – возникновение модуляционной неустойчивости в первоначально немодулированной, синусоидальной волне, в которой малые возмущения её амплитуды и фазы нарастают и формируется сильно модулированная волна. В др. случае модуляция не растёт, но обостряется профиль модулирующего возмущения (огибающей). В обоих случаях возможно формирование волн с неизменным профилем модуляции (стационарные волны огибающих), в т. ч. уединённых волновых пакетов (солитонов огибающей) и перепадов интенсивности (ударных волн огибающей). В нелинейной оптике известны «светлые» и «тёмные» солитоны, которые применяются для передачи сигналов в оптич. волокнах.
Понятие модуляции можно использовать и для негармонических сильно нелинейных колебаний и волн, параметры которых (период, амплитуда) медленно изменяются во времени и пространстве. При этом немодулированная волна имеет вид $F(ωt-kx, Q)$, где $F$ – периодич. функция, $Q$ – один или неск. параметров, характеризующих волну, напр. её амплитуда или период. Модулированная волна такого типа имеет вид $F[θ(x, t), Q(x, t)]$. С некоторой долей условности можно говорить о модуляции уединённой нелинейной волны в виде бегущего импульса – солитона, если его параметры (амплитуда и длина) медленно изменяются по мере распространения.
Математич. описание модулированных колебаний и волн основано на асимптотич. методах теории возмущений, которая применяется к дифференциальным (или более общим) уравнениям, содержащим к.-л. малый параметр. Хотя такие методы могут быть различными, практически во всех случаях закон модуляции находится из условия, что поправки к нему остаются малыми (нерезонансными) на достаточно протяжённых интервалах времени и пространства.