КВА́НТОВЫЕ ПАРАДО́КСЫ

КВА́НТОВЫЕ ПАРАДО́КСЫ, не­обыч­ное по­ве­де­ние кван­то­вых объ­ек­тов, про­ти­во­ре­ча­щее при­выч­ным пред­став­ле­ни­ям, ос­но­ван­ным на т. н. здра­вом смыс­ле. Па­ра­док­сы по­яв­ля­ют­ся в фи­зич. экс­пе­ри­мен­тах и мо­гут иг­рать по­ло­жи­тель­ную роль в раз­ви­тии фи­зич. тео­рии. Наи­бо­лее из­вест­ные па­ра­док­сы: Эйн­штей­на – По­доль­ско­го – Ро­зе­на па­ра­докс и па­ра­докс шрё­дин­ге­ров­ско­го ко­та. Па­ра­док­сы час­то воз­ни­ка­ли на ран­нем эта­пе раз­ви­тия кван­то­вой тео­рии.

Рис. 1. Схема интерференции Юнга: вероятность обнаружения одинокой частицы за экраном с двумя узкими щелями описывается гармонической функцией.

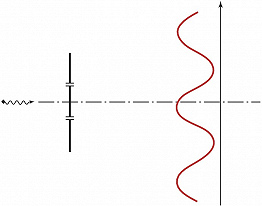
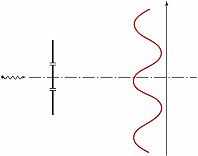
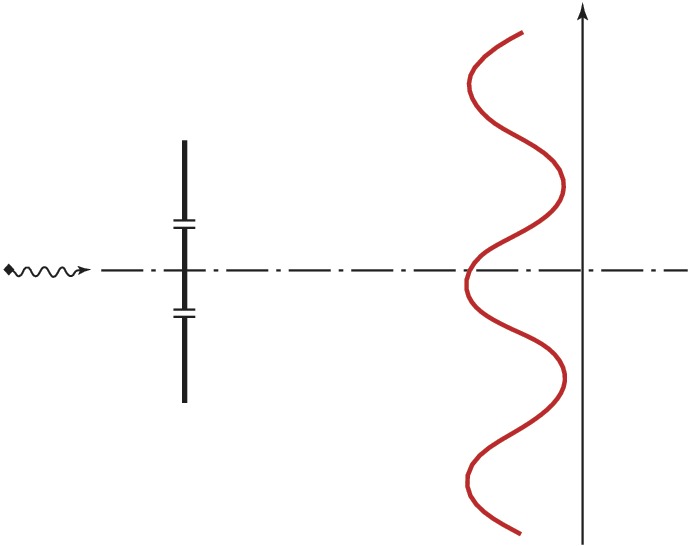
Не­де­ли­мая кван­то­вая час­ти­ца мо­жет прой­ти толь­ко че­рез од­ну из двух ще­лей не­про­зрач­но­го эк­ра­на (рис. 1), од­на­ко при мно­го­крат­ном её про­пус­ка­нии по­чер­не­ние чув­ст­ви­тель­ной фо­то­плас­тин­ки име­ет ха­рак­тер­ные ин­тер­фе­рен­ци­он­ные ми­ни­му­мы и мак­си­му­мы. Это оз­на­ча­ет, что, про­хо­дя че­рез од­ну из ще­лей, час­ти­ца как-то «уз­на­ёт» о су­ще­ст­во­ва­нии вто­рой ще­ли. В ос­но­ве объ­яс­не­ния это­го про­ти­во­ре­чия ле­жит один из гл. прин­ци­пов кван­то­вой ме­ха­ни­ки – кор­пус­ку­ляр­но-вол­но­вой дуа­лизм, в со­от­вет­ст­вии с ко­то­рым мик­ро­объ­ек­там од­но­вре­мен­но при­су­щи кор­пус­ку­ляр­ные и вол­но­вые свой­ст­ва. Как вол­на час­ти­ца мо­жет ис­пы­ты­вать ин­тер­фе­рен­цию, а как час­ти­ца она долж­на бы про­хо­дить толь­ко че­рез од­ну щель.

К. п. мо­гут быть так­же свя­за­ны с кван­то­вой не­ло­каль­но­стью, ко­то­рая яр­ко про­яв­ля­ет­ся при на­блю­де­нии за по­ве­де­ни­ем кор­ре­ли­ро­ван­ных час­тиц. Рас­смот­рим, напр., элек­трон-по­зи­трон­ную па­ру. Её ро­ж­де­ние из ва­куу­ма мо­жет про­ис­хо­дить под дей­ст­ви­ем ин­тен­сив­ных све­то­вых им­пуль­сов в силь­ном маг­нит­ном по­ле. Сум­мар­ный мо­мент ко­ли­че­ст­ва дви­же­ния час­тиц (спин) – ну­ле­вой, од­на­ко у ка­ж­дой из час­тиц он слу­ча­ен (+¹/₂ ли­бо –¹/₂), при­чём до мо­мен­та из­ме­ре­ния спи­на оп­ре­де­лён­но­го его зна­че­ния ап­ри­ор­но не су­ще­ст­ву­ет. Зна­че­ние из­ме­ряе­мой ве­ли­чи­ны по­яв­ля­ет­ся лишь в мо­мент её ре­ги­ст­ра­ции при взаи­мо­дей­ст­вии с из­ме­ри­те­лем. При этом вто­рая час­ти­ца мгно­вен­но по­лу­ча­ет оп­ре­де­лён­ное зна­че­ние спи­на про­ти­во­по­лож­но­го зна­ка, на ка­ком бы боль­шом рас­стоя­нии ни на­хо­ди­лись раз­ле­тев­шие­ся час­ти­цы па­ры. При та­ком не­обыч­ном по­ве­де­нии на­ру­ша­ют­ся т. н. не­ра­вен­ст­ва Бел­ла, что на­дёж­но под­тверж­де­но эк­спе­ри­мен­таль­но. Не­ра­вен­ст­ва Бел­ла – чис­ло­вые не­ра­вен­ст­ва, свя­зы­ваю­щие ста­ти­стич. ха­рак­те­ри­сти­ки из­ме­ря­е­мых ве­ли­чин, ко­то­рые рас­счи­ты­ва­ют­ся на ос­но­ве ло­каль­ной ве­ро­ят­но­ст­ной тео­рии, со­дер­жа­щей скры­тые па­ра­мет­ры. Ес­ли скры­тые па­ра­мет­ры су­ще­ст­ву­ют, то не­ра­вен­ст­ва вы­пол­ня­ют­ся. На­ру­ше­ние не­ра­венств оз­на­ча­ет не­ло­каль­ность эф­фек­та.

По­пыт­ки при­ме­нить кван­то­вый прин­цип су­пер­по­зи­ции со­стоя­ний к клас­сич. объ­ек­там при­во­дят к па­ра­док­сам ти­па шрё­дин­ге­ров­ско­го ко­та. Па­ра­докс с ко­том, сфор­му­ли­ро­ван­ный Э. Шрё­дин­ге­ром, за­клю­ча­ет­ся в сле­дую­щем. В не­про­зрач­ном ящи­ке на­хо­дят­ся кот и кол­ба с ядо­ви­тым га­зом и есть уст­рой­ст­во, ко­то­рое мо­жет опус­тить мо­ло­ток и раз­бить кол­бу, то­гда кот по­гиб­нет. Ра­бо­та уст­рой­ст­ва (дей­ст­вие мо­лот­ка) за­пус­ка­ет­ся в ре­зуль­та­те ра­дио­ак­тив­но­го рас­па­да яд­ра. В на­чаль­ном со­стоя­нии все яд­ра це­лы и кот жив. Ка­кое со­стоя­ние ко­та бу­дет че­рез вре­мя боль­шее, чем пе­ри­од по­лу­рас­па­да яд­ра? Су­ще­ст­ву­ют две воз­мож­но­сти. Ес­ли мо­ло­ток не упал и кол­ба не раз­би­та, то кот жив. Про­ти­во­по­лож­ный слу­чай – мо­ло­ток раз­бил кол­бу и кот мёртв. Па­ра­докс со­сто­ит в том, что кот (мак­ро­ско­пич. объ­ект) с кван­то­вой точ­ки зре­ния мо­жет од­но­вре­мен­но быть и жи­вым, и мёрт­вым (его со­стоя­ние мы уз­на­ем толь­ко по­сле от­кры­тия ящи­ка). Од­на­ко для мак­ро­ско­пич. объ­ек­та это не­обыч­ное су­пер­по­зи­ци­он­ное со­стоя­ние. Су­пер­по­зи­ци­ей яв­ля­ют­ся со­стоя­ния «не­раз­би­тая кол­ба, жи­вой кот» и «раз­би­тая кол­ба, мёрт­вый кот».

Рис. 2. Двухуровневая система (a); трёхуровневая конфигурация (б). Исходно атом находится в состоянии 1. Резонансное излучение на частоте перехода 1→2 может перевести атом в состояние 2, однако в...

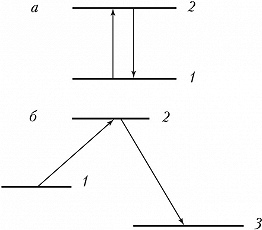
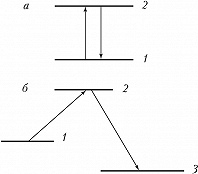
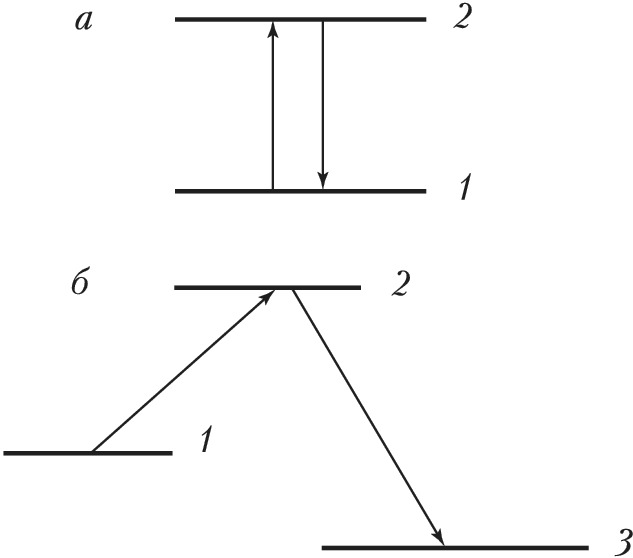
В тео­рии кван­то­вых из­ме­ре­ний воз­ни­ка­ет т. н. кван­то­вый па­ра­докс Зе­но­на. Эф­фект по­лу­чил на­зва­ние по ана­ло­гии с из­вест­ной апо­ри­ей Зе­но­на Элей­ско­го, со­глас­но ко­то­ро­му ис­пу­щен­ная из лу­ка стре­ла не мо­жет дос­тичь це­ли, по­сколь­ку в ка­ж­дый мо­мент вре­ме­ни она за­ни­ма­ет часть про­стран­ст­ва, рав­ную её раз­ме­ру, т. е. по­ко­ит­ся. Кван­то­вый па­ра­докс Зе­но­на фор­му­ли­ру­ет­ся так: по­вто­ряю­щие­ся (в пре­де­ле – не­пре­рыв­ные) из­ме­ре­ния кван­то­вой сис­те­мы пре­пят­ст­ву­ют её пе­ре­хо­ду в др. со­стоя­ние. Двух­уров­не­вый атом в по­ле ре­зо­нанс­но­го из­лу­че­ния пе­рио­ди­че­ски со­вер­ша­ет пе­ре­хо­ды с ниж­не­го уров­ня на верх­ний и об­рат­но (рис. 2, а). Од­на­ко ес­ли за со­стоя­ни­ем ато­ма ус­та­но­вить на­блю­де­ние, то, не­смот­ря на на­ли­чие ре­зо­нанс­но­го из­лу­че­ния, пе­ре­хо­ды за­мед­ля­ют­ся и да­же пол­но­стью пре­кра­ща­ют­ся. Сис­те­ма «за­мо­ра­жи­ва­ет­ся» на уров­не 1 при на­ли­чии воз­мож­но­сти её мо­мен­таль­но­го пе­ре­хо­да (из­ме­ре­ния) с уров­ня 2 на уро­вень 3 (рис. 2, б). Это при­мер реа­ли­за­ции па­ра­док­са Зе­но­на при не­пре­рыв­ном из­ме­ре­нии – сле­же­нии за ис­пус­ка­ни­ем спон­тан­ных фо­то­нов на час­то­те ω₂₃. Хо­тя са­мо­го сле­же­ния фак­ти­че­ски мо­жет и не быть. Важ­но, что име­ет­ся по­тен­ци­аль­ная воз­мож­ность та­ко­го сле­же­ния. Мы име­ем воз­мож­ность двух по­сле­до­ва­тель­ных пе­ре­хо­дов: 1→2→3. Ка­за­лось бы, чем «лег­че» пе­ре­ход 2→3, тем луч­ше для все­го кас­ка­да двух про­цес­сов. Но это не так: пе­ре­ход 2→3 тор­мо­зит пе­ре­ход 1→2, т. е. пе­ре­хо­ды не яв­ля­ют­ся не­за­ви­си­мы­ми. Па­ра­док­саль­ность си­туа­ции со­сто­ит в том, что воз­мож­ность на­блю­де­ния за сис­те­мой кар­ди­наль­но ме­ня­ет её по­ве­де­ние, а в по­сле­до­ва­тель­ном кас­ка­де двух, ка­за­лось бы, не­за­ви­си­мых про­цес­сов вто­рой по вре­ме­ни мо­жет ра­ди­каль­но вли­ять на пер­вый.