ДИФРА́КЦИЯ СВЕ́ТА
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ДИФРА́КЦИЯ СВЕ́ТА, в узком, но наиболее употребительном смысле – огибание лучами света границы непрозрачных тел (экранов), проникновение света в область геометрич. тени. В широком смысле Д. с. – проявление волновых свойств света в условиях перехода от волновой оптики к геометрической. Наиболее рельефно Д. с. проявляется в областях резкого изменения плотности потока лучей: на границах геометрич. тени, вблизи фокуса линзы и др.
Д. с. тем слабее, чем меньше длина волны $λ$ света. Красный свет сильнее отклоняется на границе тел, чем фиолетовый. Поэтому последовательность цветов в спектральном разложении белого света, вызванном дифракцией, получается обратной по сравнению с получающейся при разложении света в призме за счёт дисперсии. Это различие часто бывает определяющим при выяснении природы мн. атмосферных оптич. явлений.
Проникновение света в область геометрич. тени было известно уже в 17 в.; так, Ф. М. Гримальди описал это явление в своём трактате, вышедшем в 1665. Однако объяснение Д. с. было дано лишь в 19 в. Тогда были сформулированы две, казалось бы, совершенно разные концепции Д. с. T. Юнг (1800) предположил, что Д. с. обусловлена поперечной диффузией волновых фронтов световых волн. Чередование тёмных и светлых полос на границе тени и света он считал результатом интерференции падающей плоской волны и вторичной, излучаемой границей.
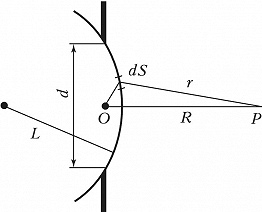
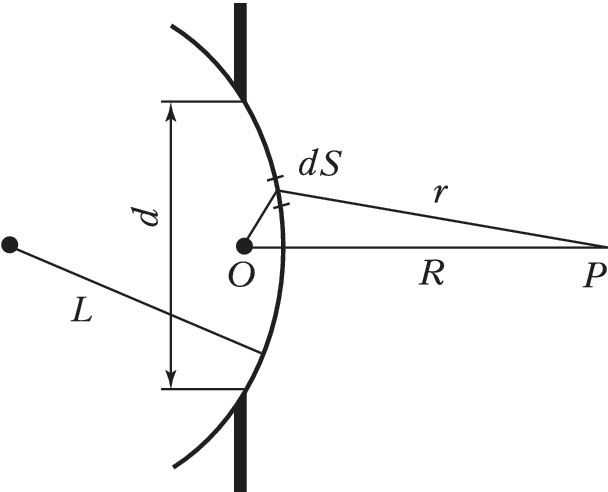
В приближённой теории О. Френеля (1815–18) Д. с. считалась результатом интерференции вторичных волн (см. Гюйгенса – Френеля принцип). Несмотря на недостатки, эта теория сохранила своё значение и служит основой расчётов дифракционных эффектов в инструментальной оптике. В теории Френеля амплитуда $u_P$ светового поля в точке наблюдения $P$ (рис. 1) слагается из парциальных амплитуд сферич. волн, испускаемых всеми элементами $dS$ поверхности $S$, не закрытой экраном. Его метод вычисления освещённости за экраном заключался в разбиении поверхности $S$, совмещённой с фронтом падающей волны, на т. н. Френеля зоны, расстояния от края которых до точки $P$ отличаются на $λ/2$. Поэтому соседние зоны вносят в поле $u_Р$ вклады противоположных знаков, взаимно компенсирующие друг друга. Освещённость в точке $P$ зависит от местоположения и размера отверстия. Эта зависимость определяется количеством зон, доступных видению из точки $P$: если открыто чётное число зон, то в центре дифракционной картины получается тёмное пятно (рис. 2,б), при нечётном числе зон – светлое (рис. 2,а).
Метод Френеля также качественно объясняет причину освещения в области геометрич. тени круглого экрана: светлый центр (т. н. пятно Пуассона) создаётся вторичными волнами первой кольцевой зоны Френеля, окружающей экран. Метод расчёта освещённости за системой экранов с использованием зон Френеля положен в основу теории зонных пластинок.
При расчётах различают два случая Д. с. – дифракция Френеля и дифракция Фраунгофера – в зависимости от соотношения между $R,\text{ } L \text{ и } d$. [Здесь $L$ – радиус кривизны поверхности $S$, не закрытой экраном, $d$ – поперечный размер отверстия, $R$ – расстояние от точки наблюдения до центра $O$ диафрагмы (отверстия), рис. 1.] Дифракция Фраунгофера имеет место, когда $kd_2/l≪1$, т. е. $d≪\sqrt {l\lambda}$, где $𝑘$ – волновое число, $1/l=1/R+1/L$ (дифракция в дальней зоне). Если источник света расположен далеко от экрана, то фронт его волны в отверстии почти плоский $(L→∞)$, и тогда $d≪\sqrt {R\lambda}$. Дифракция Фраунгофера наблюдается, когда размер отверстия значительно меньше зоны Френеля. Картина дифракции в этом случае характеризуется угловым распределением интенсивности потока, расходящегося с углом расходимости $φ∼λ/d$. Картина дифракции Фраунгофера не меняется, если экраны превратить в диафрагмы, а последние – в экраны. Из этого следует, в частности, что маленький экран может служить фокусирующей системой в той же степени, что и отверстие в камере-обскуре.
Дифракция Френеля ($𝑘d^2/l≫1$, дифракция в ближней зоне) обусловлена изогнутостью дифрагирующего волнового фронта или его относительно большими угловыми размерами $d/r≫λ/d$, воспринимаемыми из точки наблюдения $P$ ($r$ – расстояние от $P$ до элемента поверхности $dS$). Дифракция Френеля наблюдается, когда размер отверстия сравним с размером зоны Френеля $d≈\sqrt {R\lambda}$. Расчёт этого случая сложен, он требует применения спец. функций даже при простейшей геометрии обрезания волновых фронтов.
Математически полное построение теории Френеля выполнил Г. Кирхгоф (1882). Однако в его теории не учитываются векторный характер световых волн и свойства самого материала экрана.
В строгих расчётах Д. с. рассматривается как граничная задача рассеяния света. Её точные решения позволяют выяснить пределы применимости теории Френеля – Кирхгофа и обосновывают представления Юнга. Из решений следует, что свет проникает в область тени сильнее, чем предсказано этой теорией. Световое поле вдали от острого края экрана в области тени такое же, как если бы край был источником граничной волны, что согласуется с представлениями Юнга. На самом деле, край – не бесконечно тонкий источник, хотя при приближении к нему плотность светового потока растёт. По этой причине глазу, аккомодированному на край, он кажется светящейся линией. Причём, несмотря на то что радиусы закругления краёв реальных экранов велики по сравнению с $λ$, дифракционные картины почти не зависят от формы краёв и их размеров: даже стеклянная пластинка радиусом в неск. метров, изогнутого края которой касается световая волна, создаёт структуру полос того же вида, что и лезвие бритвы.
Д. с. может проявляться и без эффекта резких границ, при плавных пространственных изменениях потоков светового поля. Напр., расплывание пучка при его распространении обусловлено дифракционной расходимостью. Расплывание пучков – яркое проявление концепции Юнга диффузии волновых фронтов.
Задачи диффузионной Д. с. связаны с исследованием распространения света в средах с крупномасштабными (по сравнению с $λ$) неоднородностями диэлектрической проницаемости: в турбулентных средах, в голографических системах, при дифракции света на ультразвуке и др. В этих случаях Д. с. часто неотделима от сопутствующей ей рефракции света.
Д. с. играет важную практич. роль: она ограничивает разрешающую способность микроскопов и телескопов, добротность открытых резонаторов и др. В лазерной технике Д. с. определяются свойства полей излучения (см. Нелинейная оптика).