ДИАГРА́ММА СОСТОЯ́НИЯ
-
Рубрика: Физика
-
-
Скопировать библиографическую ссылку:
ДИАГРА́ММА СОСТОЯ́НИЯ, графич. изображение состояний физич. или физико-химич. системы, обычно в декартовой системе координат, на осях которой отложены численные значения определённых параметров состояния системы. Понятие состояния системы (вещества или излучения) – одно из наиболее общих и фундаментальных в физике – определяется набором составляющих эту систему микроскопич. структурных единиц (атомов, молекул и др.), а также характером взаимодействий между ними и совокупностью макроскопических, внешних по отношению к системе условий (значениями объёма, темп-ры $T$, давления $p$ и т. п.). Примерами состояний являются агрегатные состояния вещества (твёрдая, жидкая и газообразная фазы), разл. структурные модификации вещества, разл. электрические (проводник, диэлектрик, полупроводник, сверхпроводник), магнитные (диа-, пара- или ферромагнетики, спиновые стёкла) и др. состояния. Д. с. называют также диаграммой фазовой, однако понятие «Д. с.» является более широким.
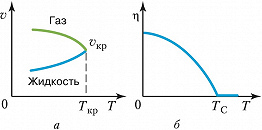
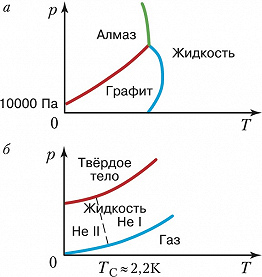
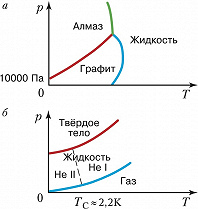
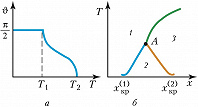
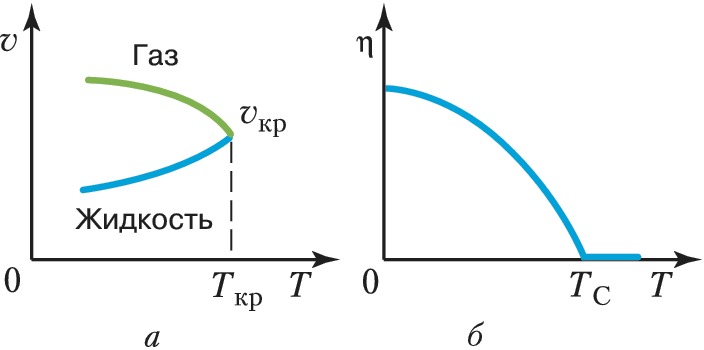
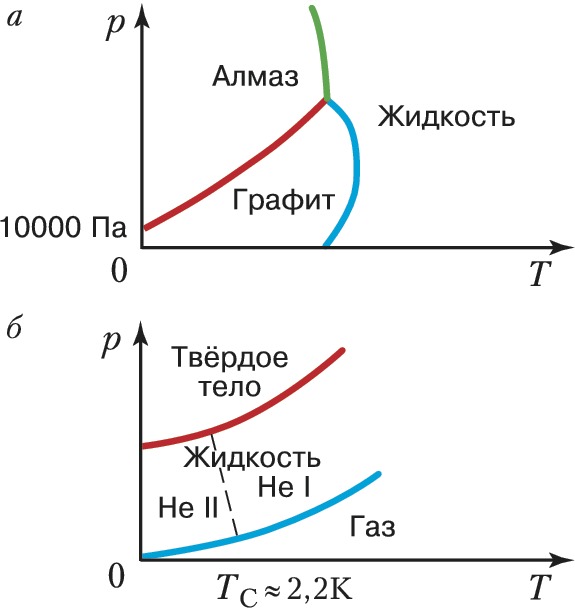
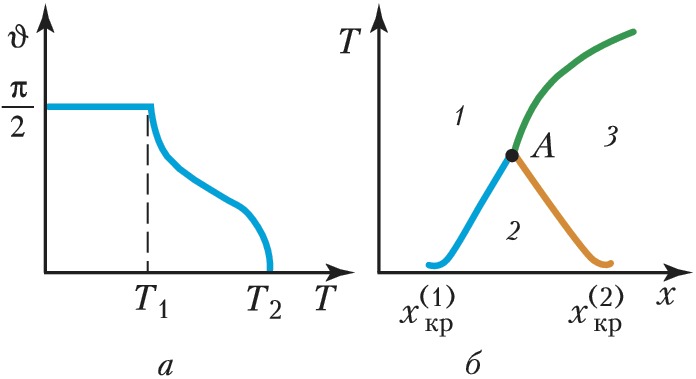
Д. с. отображает тот факт, что одно и то же вещество может находиться в разл. состояниях в зависимости от внешних условий: значений $T$ (рис. 1) и/или $p$ (рис. 2), величины и/или направления электрических $E$ и/или магнитных $H$ полей, концентраций $x$ образующих вещество атомов химич. элементов или молекул и т. п. Качественно состояния (фазы), как правило, отличаются друг от друга значениями параметра порядка. Д. с. указывает условия, при которых возможны взаимные переходы между состояниями (фазами) – фазовые переходы 1-го (рис. 1, а; 2) или 2-го (рис. 1, б; 3) рода в зависимости от характера изменения параметра порядка – непрерывного или скачкообразного. Напр., агрегатные состояния вещества различаются не только значениями удельного объёма $v$ (напр., для жидкости и газа $v_ж \lt v_г$ при $T \lt T_{кр}$), но и характером упорядочения частиц (или, в более общем случае, симметрией состояния в целом). Так, в газообразной фазе значение $v$ очень велико, к.-л. порядок в расположении частиц отсутствует; в конденсированном веществе значение $v$ мало, и в жидкой и твёрдой фазах оно примерно одинаково, однако в жидкостях имеется лишь ближний порядок, а для твёрдых тел (кристаллов) характерен дальний и ближний порядок. Переходы между этими тремя фазами являются фазовыми переходами 1-го рода. В общем случае при изменении значений $T$ и $p$ возможны также и структурные фазовые переходы между разл. твёрдыми модификациями одного и того же вещества (рис. 2; см. Полиморфизм).
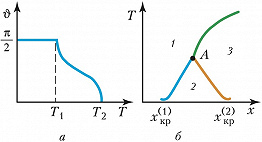
Переходы из проводящего в сверхпроводящее состояние, из парамагнитного в ферромагнитное, а также из вязкого в сверхтекучее являются фазовыми переходами 2-го рода и соответствуют непрерывным кривым на Д. с., которые, как правило, имеют универсальный вид, подобный приведённому на рис. 1, б. Магнитные фазовые переходы в разл. веществах описываются более разнообразными Д. с. (рис. 3). Физич. системы с несколькими взаимодействующими между собой параметрами порядка (напр., сосуществование ферромагнитного и сверхпроводящего состояний) описываются ещё более сложными Д. с.
С развитием эксперим. возможностей изучения состояния вещества при высоких значениях $T$ и $p$ как в земных, так и в космич. лабораториях появилась новая область исследований – физика экстремальных состояний вещества. Для наглядного изображения эволюции Вселенной используется Д. с. материи начиная от гипотетич. момента Большого Взрыва; при этом последовательность состояний определяется темп-рой Вселенной $T_{Вс}$, однозначно связанной с её масштабным фактором («радиусом») и временем её эволюции. В разл. диапазонах значений $T_{Вс}$ реализуются термодинамически устойчивые состояния (фазы) материи, в т. ч. физич. вакуум, кварк-глюонная плазма, адронная материя, водородно-гелиевая плазма и др.
Существуют также Д. с. как графич. формы уравнения состояния (термодинамич. диаграммы), выражающие зависимость к.-л. термодинамич. функции $f$ от двух термодинамич. параметров, напр. от темп-ры и удельного объёма или от энтропии и энтальпии. На таких диаграммах приводится семейство изолиний $f$ = const.
Изучение Д. с. представляет большой теоретич. и прикладной интерес в связи с фундам. проблемой прогнозирования изменения свойств материи в зависимости от разл. внешних условий; напр., при решении вопросов, связанных с синтезом новых материалов с заранее заданными физико-химич. свойствами, в решении ряда проблем астрофизики и космологии, планетологии, геофизики.
-
Рис. 1. Диаграммы состояния: а – в координатах T – v [двухфазное состояние сосуществования жидкости и насыщенного пара (при фиксированном давлении p) переходит в однофазное при критической температуре Т = Ткр]; б – в координатах T – η (параметр порядка η максимален при Т = 0 и обращается в нуль при критической температуре Т = ТC). -
Рис. 2. Диаграммы T – p состояний углерода (а) и гелия (б); жидкие фазы Не I и сверхтекучего Не II разделены на диаграмме пунктирной линией. -
Рис. 3. Диаграммы магнитных состояний вещества: а – редкоземельный магнетикс параметром порядка ϑ – углом ориентации магнитного момента относительно кристаллографической оси. Зависимость ϑ от Т обладает двумя точками фазовых переходов 2-го рода Т1, Т2; б – сплав EuxSr1-xS: 1 – парамагнитное состояние, 2 – состояние спинового стекла, 3 – ферромагнитное состояние; – критические значения концентрации Eu, соответствующие фазовым переходам между состояниями при Т=0; А – тройная точка сосуществования всех трёх состояний.
