ОРИЕНТА́ЦИЯ
-
Рубрика: Математика
-
-
Скопировать библиографическую ссылку:
ОРИЕНТА́ЦИЯ (от франц. orientation, букв. – направление на восток, от лат. oriens – восток) в математике, обобщение понятия направления на прямой на более сложные геометрич. фигуры.
Ориентация на прямой
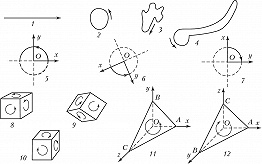
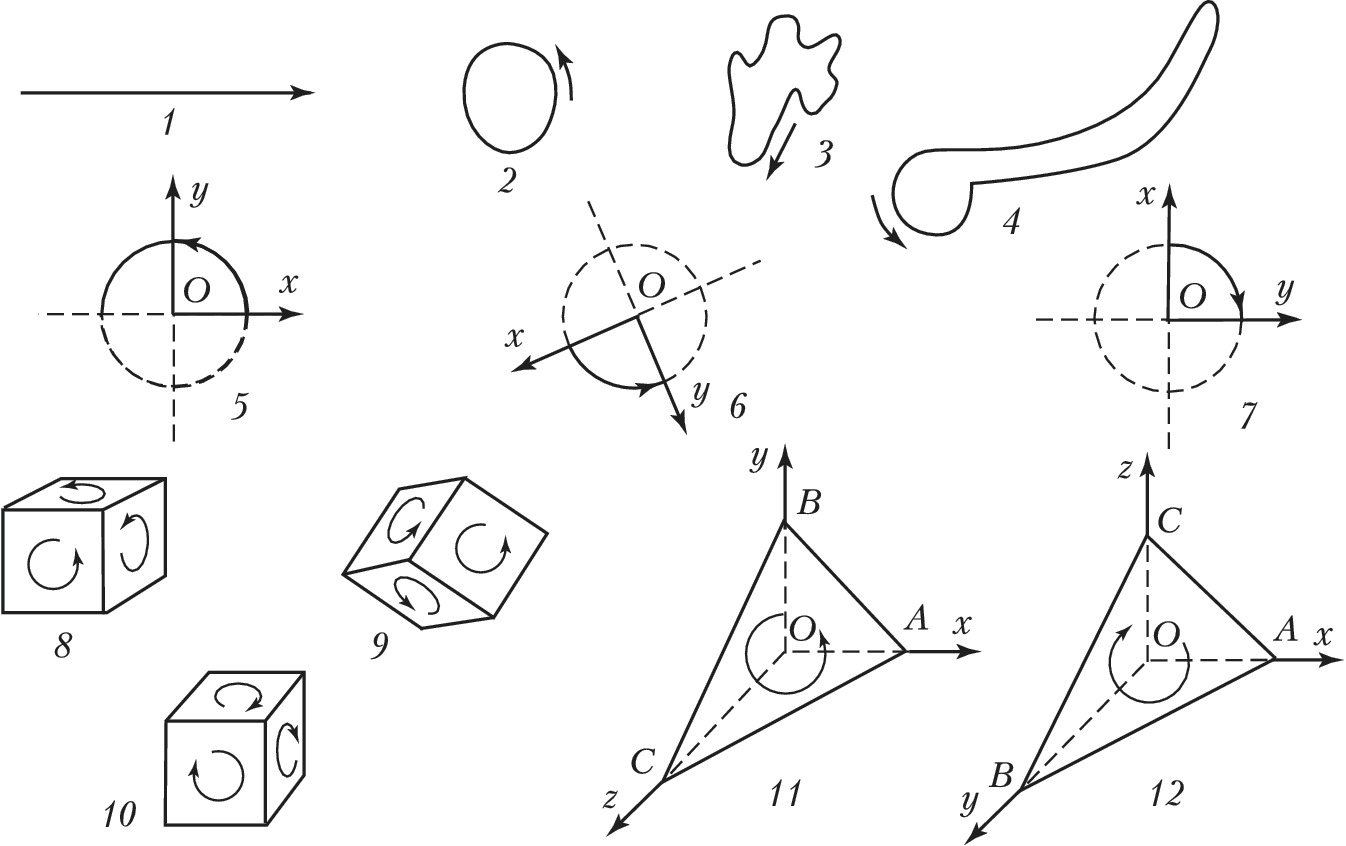
Точка может двигаться по прямой в двух противоположных направлениях. Напр., на горизонтальной прямой возможно или движение справа налево, или движение слева направо. Прямая вместе с указанием определённого направления на ней называется ориентированной прямой (рис., 1).
Ориентация на плоскости
Пусть к.-л. часть плоскости ограничена простой замкнутой кривой (т. е. замкнутой кривой без кратных точек). Эту кривую можно ориентировать двумя разными способами: против часовой стрелки (рис., 2) или по часовой стрелке (рис., 3). При ориентации кривой ориентируется и ограниченная ею часть плоскости. Две простые замкнутые кривые на плоскости считаются ориентированными одинаково, если при обходе этих кривых по указанным направлениям ограниченные ими части плоскости остаются с одной и той же стороны от кривой (в обоих случаях или справа, или слева). Напр., на рис., 2 и 4 кривые ориентированы одинаково, а кривая на рис., 3 – противоположно им. На плоскости достаточно выбрать О. одной простой замкнутой кривой, чтобы тем самым определилась соответствующая О. всех остальных таких кривых, лежащих на той же плоскости. Плоскость вместе с определённым выбором О. лежащих на ней простых замкнутых кривых называется ориентированной плоскостью. О. плоскости может быть также задана при помощи выбора систем декартовых координат. Если на плоскости выбраны оси координат $Ox$ и $Oy$ с определёнными положительными направлениями на них, то этому выбору соответствует О. плоскости, при которой окружность с центром в начале координат ориентирована в направлении от положительного направления оси $Ox$ к положительному направлению оси $Oy$. Напр., системы координат на рис., 5 и 6 определяют одну и ту же О. плоскости. Система координат на рис., 7 определяет противоположную О. плоскости.
Координаты $(x,y)$ и $(x',y')$ в двух декартовых системах координат на плоскости связаны соотношениями $$x'=a_{11}x+a_{12}y+b_1,\\ y'=a_{21}x+a_{22}y+b_2,$$где определитель $$\Delta= \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{vmatrix} $$отличен от нуля. Системы координат $(x,y)$ и $(x',y')$ ориентированы одинаково, если $\Delta \gt 0$, и противоположно, если $\Delta \lt 0$. Это обстоятельство можно использовать для строгой аналитич. теории О. на плоскости. Множество $D$ всех декартовых систем координат распадается на два подмножества $D'$ и $D''$ так, что в пределах $D'$ (и в пределах $D''$) все системы координат связаны преобразованиями с $\Delta \gt 0$, а любая система координат из $D'$ связана системой координат из $D''$ преобразованием с $\Delta \lt 0$. Выбрать О. на плоскости – это и значит выбрать одно из множеств $D'$ или $D''$. Выбор О. на плоскости определяет знак расположенных на плоскости углов и площадей, ограниченных ориентированными замкнутыми кривыми. Напр., формула $$S=\frac{1}{2}\int_C xdy-ydx$$площади $S$, ограниченной замкнутой кривой $C$, ориентированной в направлении, указанном стрелкой, в случае правой системы координат (рис., 5 и 6) приведёт к положительным площадям фигур на рис., 2 и 4 и к отрицательной для фигуры на рис., 3. Наоборот, в левой системе координат (рис., 7) вычисленная по формуле площадь $S$ фигуры на рис., 3 будет положительна, а площади фигур на рис., 2 и 4 – отрицательны.
Ориентация на поверхности
Подобно тому, как выше была определена О. плоскости, может быть определена О. любой поверхности, делящей пространство на две части (напр., сферы). Для этого рассматриваются части поверхности, ограниченные простыми замкнутыми линиями. Ориентировать такую часть поверхности – это значит выбрать определённую О. ограничивающей её кривой. Две части поверхности называются ориентированными одинаково, если при обходе ограничивающих эти части поверхности кривых в указанных направлениях сами части поверхности остаются с одной и той же стороны. Напр., поверхности двух кубов на рис., 8 и 9 ориентированы одинаково, а поверхность третьего (рис., 10) – противоположным образом. Поверхность вместе с определённой О. частей, ограниченных простыми замкнутыми кривыми, называется ориентированной поверхностью. Не всякая поверхность может быть ориентирована. Примером неориентируемой поверхности является Мёбиуса лист; см. также Клейна поверхность. Однако поверхность, ограничивающая часть пространства, всегда принадлежит к числу ориентируемых.
Ориентация пространства
Пусть замкнутая поверхность ограничивает определённую часть пространства. Говорят, что такая поверхность ориентирована правым образом, если части этой поверхности, наблюдаемые снаружи, представляются ориентированными против часовой стрелки, подобно кубам на рис., 8 и 9. Наоборот, О. замкнутой поверхности, ограничивающей часть пространства, считается левой, если её части ориентированы при наблюдении снаружи по часовой стрелке, подобно кубу на рис., 10. Выбор определённой О. замкнутых поверхностей без самопересечений называется О. самого трёхмерного пространства. Таким образом, существуют две О. трёхмерного пространства: правая и левая. О. пространства можно установить также при помощи выбора системы декартовых координат. Если выбраны оси координат $Ox$, $Oy$, $Oz$ с определёнными положительными направлениями на них, то соответствующая О. пространства определяется следующим условием: рассматривается тетраэдр $OABC$ с вершиной $O$ в начале координат и с вершинами $A$, $B$, $C$ соответственно на положительных лучах осей $Ox$, $Oy$, $Oz$ (рис., 11, 12), треугольник $ABC$, лежащий на поверхности этого тетраэдра, ориентируется в порядке $ABC$ (т. е. от оси $Ox$ к оси $Oy$ и затем к оси $Oz$); этим определяется О. поверхности тетраэдра, а следовательно, и самого пространства. Выбор осей на рис., 11 соответствует правой О. пространства, выбор осей на рис., 12 – левой О. пространства. Также сами системы координат в пространстве разделяются на правые и левые. От выбора О. пространства зависят знаки объёмов, ограниченных ориентированными поверхностями, смысл векторного произведения двух векторов и т. п.
Понятие О. распространяется и на многомерные пространства.